Задачи на циклы тепловые машины
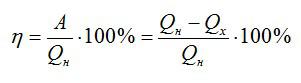
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
Подставляем значения и вычисляем:
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
Теперь можно рассчитать КПД:
Или, умножая на 100, получаем значение КПД в процентах:
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
По условию:
Вычислим сначала работу, а затем КПД:
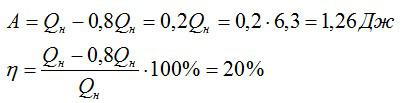
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
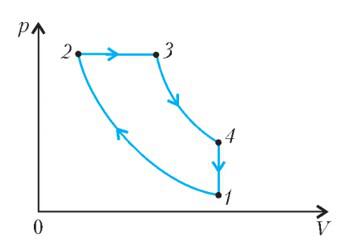
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
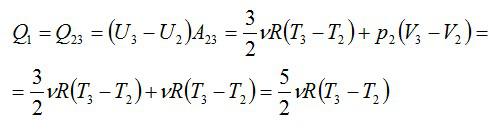
Аналогично:
Получим результат:
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
Отсюда:
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
Источник
Тема. Решение задач по теме “Физические принципы работы тепловых машин. Циклы тепловых машин. К.п.д. тепловых двигателей”.
Цели:
- помочь учащимся сформулировать принципы работы тепловой машины, разобраться в ее принципиальном, с точки зрения физики, устройстве;
- научить вычислять полезную работу, совершенную тепловой машиной за цикл;
- освоить методы расчета к.п.д. тепловых двигателей.
Ход занятия
В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач по мере возрастания их сложности.
Прежде чем приступить к выполнению задания, следует сформулировать физические принципы работы тепловой машины, вспомнить, что работа за цикл определяется площадью под кривой цикла, определить понятие к.п.д. тепловой машины, кратко рассмотреть обратимый цикл Карно и его к.п.д., при этом обратив внимание, что значение к.п.д. обратимого цикла Карно ставит теоретический предел возможному значению к.п.д. реальной тепловой машины.
Качественные задачи
- Восходящий от поверхности земли поток воздуха представляет собой своеобразный тепловой двигатель. Укажите в нем основные части, присущие любому тепловому двигателю.
- Что является нагревателем и холодильником в ракетном двигателе?
- Станет ли к.п.д. тепловой машины равным 100 %, если трение в частях машины свести к нулю?
- Какие пути вы можете указать для повышения к.п.д. тепловых двигателей?
- Почему в качестве источников энергии затруднительно использовать внутреннюю энергию вод мирового океана и земной атмосферы?
Примеры решения расчетных задач
Задача 1.
Рабочее вещество, внутренняя энергия которого U связана с давлением P и объемом V соотношением U = kPV, совершает термодинамический цикл, состоящий из изобары, изохоры и адиабаты (рис. 1). Работа, совершенная веществом во время изобарного процесса, в m = 5 раз превышает работу внешних сил по сжатию вещества, совершенную при адиабатическом процессе. К.п.д. цикла η=1/4. Определите k.
Решение:
Подставляя (5) и (6) в (1) и решая относительно k, находим
.
Ответ: k=2,2.
Задача 2.
Рабочее вещество тепловой машины совершает цикл Карно между изотермами T и T1 (T1>T) (рис. 2). Холодильником является резервуар, температура которого постоянна и равна T2 = 200 К (T2T). Теплообмен между рабочим веществом и холодильником осуществляется посредством теплопроводности. Количество теплоты, отдаваемое в единицу времени холодильнику, q = α(T–T2), где α = 1кВт/К. Теплообмен рабочего вещества с нагревателем происходит непосредственно при T1 = 800 К. Полагая, что продолжительность изотермических процессов одинакова, а адиабатических – весьма мала, найдите температуру “холодной” изотермы T, при которой мощность тепловой машины наибольшая. Определите наибольшую мощность тепловой машины.
Решение:
Из (7) видно, что N = Nmax приК.
кВт.
Ответ: наибольшая мощность машины равна 100 кВт.
Задача 3.
В тепловой машине ν молей идеального одноатомного газа совершают замкнутый цикл, состоящий из процессов 1–>2 и 2–>3, в которых давление P газа линейно зависит от занимаемого им объема V, и изохорического процесса 3–>1 (рис. 3). Величины P0 и V0 считаются известными. Найдите:
- температуру и давление газа в точке 3;
- работу, совершенную газом за цикл;
- к.п.д. машины.
Решение:
Давление, объем и температуру в точках 1, 2 и 3 обозначим через P, V и T с соответствующими индексами.
| Поскольку на участке 2–>3 давление линейно, но зависит от занимаемого объема, то можно записать | |
| (1) | |
| Из рисунка видно, что | |
| V3=3V0, P2=P0, V2=7V0. | |
| Подставляя эти значения в (1), находим P3 | |
| (2) | |
| Из уравнения состояния идеального газа, используя (2), получаем T3. | |
| (3) | |
| Работа газа за цикл численно равна площади треугольника 123. Эту площадь можно вычислить как сумму площадей двух прямоугольных треугольников | |
| (4) | |
| Для вычисления к.п.д. цикла нужно найти количество теплоты, полученное газом. | |
| Количество тепла, полученное газом на участке 3–>1, равно | |
| (5) | |
| Покажем, что на участке цикла 1–>2 есть точка К с соответствующим объемом VK таким, что газ при VVK получает тепло, а при V>VK отдает тепло. | |
| Найдем аналитическое выражение процесса, соответствующего участку 1–>2. Как видно из рисунка, участку 1–>2 соответствует линейная функция | |
| (6) | |
| Введем обозначенияи найдем параметры k и b, воспользовавшись данными, указанными на рисунке. | |
| При x = 0, следовательно, b = 8; | |
| y = 0 0 = kx + 8, следовательно, k = -1. | |
| Таким образом, (6) представляется в виде | |
| или | |
| (7) | |
| Подставив P в виде (7) в уравнение состояния идеального газа PV = νRT, получаем | |
| (8) | |
| Из уравнения (8) в приращениях | |
| (9) | |
| С учетом полученных соотношений (7) и (9) уравнение 1-го закона термодинамики на участке 1–>2можно представить в виде | |
| (10) | |
| Из полученного уравнения видно, что на участке 1–>2 Q1K > 0 при V V0 и QK2V > 5V0, следовательно, | |
| Воспользовавшись этими значениями, найдем количество теплоты, получаемое газом на участке 1–>К, предварительно определив T1 из уравнения состояния идеального газа | |
| (11) | |
Итак, совершая полный цикл, газ получает тепло на участках 3–>1 и 1–>К. Количество полученного на этих участках тепла определяется равенствами (5) и (11).
Работа, совершенная газом за цикл, найдена в (4).
Теперь есть все данные для определения к.п.д. цикла.
Ответ: к.п.д. рассмотренного цикла равен 32 %.
Задача 4.
Идеальная холодильная машина имеет в качестве холодильника резервуар с водой при 0°С, а в качестве нагревателя – резервуар с кипящей водой. Какую работу надо совершить, чтобы превратить в лед 1 кг воды? Какое количество воды в нагревателе превратится при этом в пар? Удельная теплота плавления льда λ = 340 кДж/кг, удельная теплота парообразования воды r = 2260 кДж/кг.
Решение:
Холодильная машина работает по такому принципу: за счет внешней механической работы тепло отнимается от более холодного резервуара и передается более горячему резервуару.
Полезный эффект холодильной машины определяется количеством теплоты Qx, отобранным у охлаждаемого тела, а затраченная энергия – это внешняя работа A, совершенная над рабочим телом. Отношение
обычно называют холодильным коэффициентом.
Если холодильная машина работает по так называемому идеальному циклу – обратному циклу Карно (цикл Карно теперь обходится против часовой стрелки), то
Из этой формулы видно, что ε может быть меньше, больше или равен 100 %. Действительно, возможно построить холодильную машину, у которой разность температур нагревателя и холодильника будет больше, меньше или равна температуре холодильника.
Тот факт, что ε может быть больше 100 %, иногда вызывает вопрос – не нарушается ли при этом закон сохранения энергии. На самом деле никакого противоречия с законом сохранения энергии нет. Тепло, отработанное у охлаждаемого тела, и энергия, затраченная на совершение работы извне, вовсе не переходят друг в друга, а отдаются нагревателю (обычно у холодильных машин им является окружающая среда).
Холодильный коэффициент идеальной машины, работающей в заданном по условию задачи температурном интервале, равен
При замерзании 1 кг воды выделяется количество теплоты
Совершенная при этом работа
Нагреватель получает количество теплоты Qн
Следовательно, в пар превратится масса воды
Задачи для самостоятельной работы
1. Тепловая машина имеет коэффициент полезного действия (к.п.д.) η = 20 %. Каким станет ее к.п.д., если количество теплоты, потребляемое за цикл, увеличится на 40 %, а количество теплоты, отдаваемое холодильнику, уменьшится на 20 %?
Ответ: к.п.д. машины стал, то есть увеличился, и составляет примерно 54 %.
2. Рассчитайте к.п.д. циклов, представленных на рис. 4.
Ответ:
3. На рис. 5 показаны два замкнутых термодинамических цикла, произведенных с идеальным одноатомным газом 1–>2–>3–>4–>1 и 1–>5–>6–>4–>1. У какого из циклов коэффициент полезного действия выше? Во сколько раз?
Ответ: для второго цикла к.п.д. выше, η1=0,74η2 .
4. Найдите к.п.д. цикла, состоящего из двух изохор и двух адиабат (рис. 6). Рабочим веществом является азот. Известно, что в пределах цикла объем газа изменяется в 10 раз, то есть Vmax / Vmin=10 .
Ответ: к.п.д. цикла равен 60 %.
5. Определите к.п.д. цикла, показанного на рис. 7. Газ идеальный одноатомный. Участки 2–>3 и 4–>5 на чертеже представляют собой дуги окружностей с центрами в точках O1 и O2.
Ответ: к.п.д. цикла равен 19 %.
Рекомендуемая литература
- Бутиков Е.И., Кондратьев А.С. Физика. Т. 3. Строение и свойства вещества. – М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. – С. 142-170.
- Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 88-90.
- Готовцев В.В. Лучшие задачи по механике и термодинамике. – М.; Ростов н/Д: Издательский центр “Март”, 2004. – С. 254-268.
Источник
Подробности
Просмотров: 668
«Физика – 10 класс»
Для решения задач надо воспользоваться известными выражениями для определения КПД тепловых машин и иметь в виду, что выражение (13.17) справедливо только для идеальной тепловой машины.
Задача 1.
В котле паровой машины температура 160 °С, а температура холодильника 10 °С.
Какую максимальную работу может теоретически совершить машина, если в топке, коэффициент полезного действия которой 60 %, сожжён уголь массой 200 кг с удельной теплотой сгорания 2,9 • 107 Дж/кг?
Р е ш е н и е.
Максимальную работу может совершить идеальная тепловая машина, работающая по циклу Карно, КПД которой η = (Т1 – Т2)/Т1, где Т1 и Т2 — абсолютные температуры нагревателя и холодильника. Для любой тепловой машины КПД определяется по формуле η = A/Q1, где А — работа, совершаемая тепловой машиной, Q1 — количество теплоты, полученной машиной от нагревателя.
Из условия задачи ясно, что Q1 — это часть количества теплоты, выделившейся при сгорании топлива: Q1 = η1mq.
Тогда откуда А = η1mq(1 – Т2/Т1) = 1,2 • 109 Дж.
Задача 2.
Паровая машина мощностью N = 14,7 кВт потребляет за 1 ч работы топливо массой m = 8,1 кг, с удельной теплотой сгорания q = 3,3 • 107 Дж/кг.
Температура котла 200 °С, холодильника 58 °С.
Определите КПД этой машины и сравните его с КПД идеальной тепловой машины.
Р е ш е н и е.
КПД тепловой машины равен отношению совершённой механической работы А к затраченному количеству теплоты Qlt выделяющейся при сгорании топлива.
Количество теплоты Q1 = mq.
Совершённая за это же время работа А = Nt.
Таким образом, η = A/Q1 = Nt/qm = 0,198, или η ≈ 20%.
Для идеальной тепловой машины η < ηид.
Задача 3.
Идеальная тепловая машина с КПД η работает по обратному циклу (рис. 13.15).

Какое максимальное количество теплоты можно забрать от холодильника, совершив механическую работу А?
Р е ш е н и е.
Поскольку холодильная машина работает по обратному циклу, то для перехода тепла от менее нагретого тела к более нагретому необходимо, чтобы внешние силы совершили положительную работу.
Принципиальная схема холодильной машины: от холодильника отбирается количество теплоты Q2, внешними силами совершается работа и нагревателю передаётся количество теплоты Q1.
Следовательно, Q2 = Q1(1 – η), Q1 = A/η.
Окончательно Q2 = (A/η)(1 – η).
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основы термодинамики. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика
Насыщенный пар —
Давление насыщенного пара —
Влажность воздуха —
Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» —
Кристаллические тела —
Аморфные тела —
Внутренняя энергия —
Работа в термодинамике —
Примеры решения задач по теме «Внутренняя энергия. Работа» —
Количество теплоты. Уравнение теплового баланса —
Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» —
Первый закон термодинамики —
Применение первого закона термодинамики к различным процессам —
Примеры решения задач по теме: «Первый закон термодинамики» —
Второй закон термодинамики —
Статистический характер второго закона термодинамики —
Принцип действия тепловых двигателей. Коэффициент полезного действия (КПД) тепловых двигателей —
Примеры решения задач по теме: «КПД тепловых двигателей»
Источник