Задачи на циклы с блоками схемами
Цель: изучение алгоритмической структуры циклы, создание моделей и алгоритмов для решения практических задач.
Ход урока
I. Актуализация знаний
- Повторить понятие алгоритма, основные конструкции алгоритмического языка.
- Уметь разрабатывать математическую модель, алгоритм и блок схему решения задачи.
- Иметь понятие о языках программирования и их назначении.
- Уметь работать в среде программирования.
- Знать структуры программы.
- Уметь записывать выражения, содержащие числовые и символьные величины.
- Знать структуры операторов и особенности их работы.
- Уметь применять операторы при написании программ с линейными и ветвящимися структурами.
- Уметь на компьютере создавать и запускать программы на отладку.
II. Теоретический материал урока
Большинство практических задач требует многократного повторения одних и тех же действий, т. е. повторного использования одного или нескольких операторов. (Презентация)
Пусть требуется ввести и обработать последовательность чисел. Если чисел всего пять, можно составить линейный алгоритм. Если их тысяча, записать линейный алгоритм можно, но очень утомительно и нерационально. Если количество чисел к моменту разработки алгоритма неизвестно, то линейный алгоритм принципиально невозможен.
Другой пример. Чтобы найти фамилию человека в списке, надо проверить первую фамилию списка, затем вторую, третью и т.д. до тех пор, пока не будет найдена нужная или не будет достигнут конец списка. Преодолеть подобные трудности можно с помощью циклов.
Циклом называется многократно исполняемый участок алгоритма (программы). Соответственно циклический алгоритм — это алгоритм, содержащий циклы.
Различают два типа циклов: с известным числом повторений и с неизвестным числом повторений. При этом в обоих случаях имеется в виду число повторений на стадии разработки алгоритма.
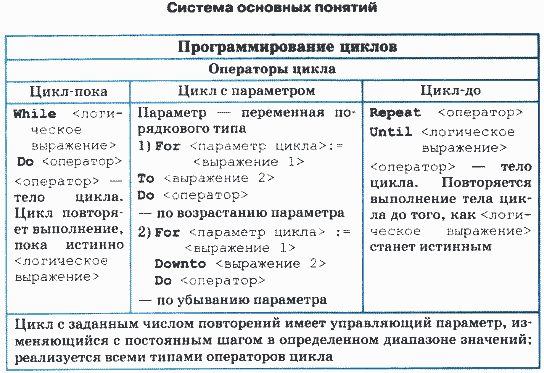
Существует 3 типа циклических структур:
- Цикл с предусловием;
- Цикл с послеусловием;
- Цикл с параметром;
Иначе данные структуры называют циклами типа «Пока», «До», «Для».
Графическая форма записи данных алгоритмических структур:
Цикл с предусловием (иначе цикл пока) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| Пока (условие) нц серия команд кц | while условие do begin серия команд; end; |
где
условие – выражение логического типа.
Цикл может не выполняться ни разу, если значение логического выражения сразу же оказывается ложь.
Серия команд, находящихся между begin и end, выполняются до тех пор, пока условие истинно.
Для того чтобы цикл завершился, необходимо, чтобы последовательность инструкций между BEGIN и END изменяла значение переменных, входящих в условие.
Цикл с постусловием (иначе цикл до) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| В алгоритмическом языке нет команды которая могла бы описать данную структуру, но ее можно выразить с помощью других команд (Например, ветвления). | repeat серия команд until условие |
где
условие – выражение логического типа.
Обратите внимание:
Последовательность инструкций между repeat и until всегда будет выполнено хотя бы один раз;
Для того чтобы цикл завершился, необходимо, чтобы последовательность операторов между repeat и until изменяла значения переменных, входящих в выражение условие.
Инструкция repeat, как и инструкция while, используется в программе, если надо провести некоторые повторяющиеся вычисления (цикл), однако число повторов заранее не известно и определяется самим ходом вычисления.
Цикл с параметром (иначе цикл для) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| Для i от а до b шаг h делай Нц Серия команд кц | h = +1 for i:= a to b do begin серия команд end; h = -1 for i:= b downto a do begin Cерия команд; end; |
где
i – параметр цикла;
a – начальное значение цикла;
b – конечное значение цикла;
h – шаг изменения параметра.
Структура данного цикла иначе называют циклом i раз.
Эта команда выполняется таким образом: параметру i присваивается начальное значение а, сравнивается с конечным значением b и, если оно меньше или равно конечному значению b, выполняется серия команд. Параметру присваивается значение предыдущего, увеличенного на величину h – шага изменения параметра и вновь сравнивается с конечным значением b.
На языке программирования Паскаль шаг изменения параметра может быть равным одному или минус одному.
Если между begin и end находится только один оператор, то операторные скобки можно не писать. Это правило работает для цикла типа «Пока» и «Для».
Рассмотрим пример решения задач с использованием данных структур
Пример.
Вычислить произведение чисел от 1 до 5 используя различные варианты цикла
Математическая модель:
Р= 1· 2· 3· 4· 5=120
Составим алгоритм в виде блок-схемы.
Для проверки правильности алгоритма заполним трассировочную таблицу.
| Шаг | Операция | Р | i | Проверка условия |
| 1 | P:=1 | 1 | ||
| 2 | i:=1; | 1 | 1 | |
| 3 | i<=5 P:=P*I i:=i+1 | 1 | 1 | 1<=5, да (истина) |
| 4 | i<=5 P:=P*I i:=i+1 | 2 | 2 | 2<=5, да (истина) |
| 5 | i<=5 P:=P*I i:=i+1 | 6 | 3 | 3<=5, да (истина) |
| 6 | i<=5 P:=P*I i:=i+1 | 24 | 4 | 4<=5, да (истина) |
| 7 | i<=5 P:=P*I i:=i+1 | 120 | 5 | 5<=5, да (истина) |
| 8 | i<=5 P:=P*I i:=i+1 | 6<=5, нет (ложь) |
Проверка условия происходит в несколько шагов: проверка условия и выполнение команд на одной из ветвей. Поэтому в трассировочной таблице записываются не команды алгоритма, а отдельные операции, выполняемые компьютером на каждом шаге.
Шаг первый: Р присваивается значение один.
Шаг второй: i присваивается значение один.
Шаг третий: при i равном единице проверяем условие один меньше или равен пяти, да, условие истинно, значит Р присваивается значение один умноженное на один, будет два. Для i: один плюс один, будет два.
Шаг четвертый: при i равном двум проверяем условие два меньше или равен пяти, да, условие истинно, значит Р присваивается значение 2 умноженное на один, будет 2. Для i: два плюс один, будет три.
Шаг пятый: при i равном трем проверяем условие три меньше или равен пяти, да, условие истинно, значит Р присваивается значение два умноженное на три, будет шесть. Для i: три плюс один, будет четыре.
Шаг шестой: при i равном четырем проверяем условие четыре меньше или равен пяти, да, условие истинно, значит Р присваивается значение шесть умноженное на четыре, будет двадцать четыре. Для i: четыре плюс один, будет пять.
Шаг седьмой: при i равном пяти проверяем условие пять меньше или равен пяти, да ,условие истинно, значит Р присваивается значение двадцать четыре умноженное на пять, будет сто двадцать. Для i: пять плюс один, будет шесть.
Шаг восьмой: при i равном шести проверяем условие шесть меньше или равен пяти, нет, условие ложно, тогда мы выходим из цикла, а в результате получаем последнее значение равное сто двадцати.
Program Pr1;
Var i: integer;
Begin
P:=1;
i:=1;
While i<=5 do
begin
P:=P*i;
i:=i+1;
end;
Write (‘P=’, P);
end.
Для цикла с постусловием построим блок-схему и трассировочную таблицу. (слайд16)
В результате получаем последнее значение равное сто двадцати на седьмом шаге
И для Цикла с параметром построим блок-схему и трассировочную таблицу. (слайд17)
В результате получаем последнее значение равное сто двадцати на шестом шаге
Задача:
Вывести на экран числа от 1 до 5 в:
- прямом порядке;
- обратном порядке.
Математическая модель:
- 1 2 3 4 5;
- 5 4 3 2 1.
Блок-схема и программа решения задачи представлена для чисел в прямом порядке и обратном порядке.
(слайд 21)
Запишем рассмотренные алгоритмы на языке программирования Паскаль.
(слайд 22)
III. Подведение итогов урока
И так мы рассмотрели следующие вопросы:
- Алгоритмическая структура цикл;
- Виды алгоритмических структур:
- Цикл с предусловием;
- Цикл с послеусловием;
- Цикл с параметром;
- Рассмотрели способы записи данных структур;
- Разобрали примеры решения задач с помощью этих структур.
Источник
Занятие 4. Графическая реализация циклического алгоритма
В рассмотрении циклического алгоритма следует выделить несколько понятий.
Тело цикла – это набор инструкций, предназначенный для многократного выполнения.
Итерация – это единичное выполнение тела цикла.
Переменная цикла – это величина, изменяющаяся на каждой итерации цикла.
Каждый цикл должен содержать следующие необходимые элементы:
- первоначальное задание переменной цикла,
- проверку условия,
- выполнение тела цикла,
- изменение переменной цикла.
Циклы бывают двух видов – с предусловием и с постусловием. В цикле с предусловием сначала проверяется условие входа в цикл, а затем выполняется тело цикла, если условие верно. Цикл с предусловием представлен на рис. 2.9. Цикл с предусловием также может быть задан с помощью счетчика. Это удобно в тех случаях, когда точно известно количество итераций. В общем виде блок-схема, реализующая цикл с предусловием, представлена ниже. Сначала задается начальное значение переменной цикла, затем условие входа в цикл, тело цикла и изменение переменной цикла. Выход из цикла осуществляется в момент проверки условия входа в цикл, когда оно не выполняется, т.е. условие ложно. Цикл с предусловием может ни разу не выполниться, если при первой проверке условия входа в цикл оно оказывается ложным.
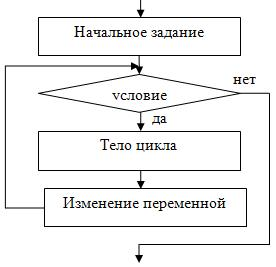
Рис.
2.9.
Циклический алгоритм с предусловием в общем виде
В цикле с постусловием сначала выполняется тело цикла, а потом проверяется условие. Циклический алгоритм с постусловием представлен на рис. 2.10.
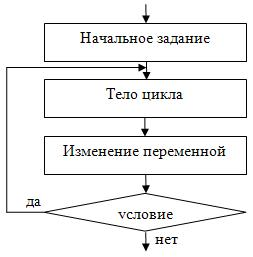
Рис.
2.10.
Циклический алгоритм с постусловием в общем виде
Если условие верно, то итерация повторяется, если же неверно, то осуществляется выход из цикла. В отличие от цикла с предусловием, любой цикл с постусловием всегда выполнится хоть раз.
Примечание. Как видно из представленных блок-схем для циклов с предусловием и постусловием, условие записывается внутри блока условия (формы ромба), как и в разветвляющемся алгоритме. Принципиальная разница между разветвляющимся и циклическим алгоритмами при графической реализации состоит в том, что в циклическом алгоритме в обязательном порядке присутствует стрелка, идущая наверх. Именно эта стрелка обеспечивает многократный повтор тела цикла.
Приведем простейшие примеры, соответствующие циклическому алгоритму.
Пример 7. Вася звонит Пете, но у Пети может быть занята линия. Составить блок-схему действий Васи в этом случае.
Решение. Когда телефонная линия занята, то необходимо снова и снова набирать номер, пока Петя не закончит предыдущий разговор, и телефонная линия не окажется вновь свободной. Блок-схема представлена на рис. 2.11.
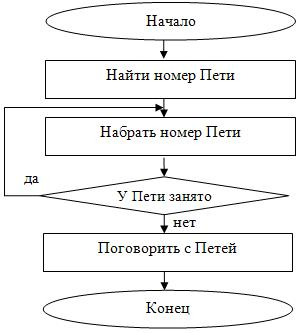
Рис.
2.11.
Блок-схема для примера 7
Здесь тело цикла состоит из одного действия “Набрать номер Пети”, т.к. именно это действие следует повторять, пока линия будет занята. Под итерацией цикла понимается очередная попытка дозвониться до Пети. Как таковой переменной цикла здесь нет, т.к. ситуация взята из жизни. Выход из цикла происходит в тот момент, когда условие “У Пети занято” стало неверным, т.е. телефонная линия свободна – действительно, нет необходимости больше набирать номер Пети. В данном примере применен цикл с постусловием, т.к. сначала необходимо набрать номер Пети, ведь иначе мы не можем ответить на вопрос – занята ли линия у Пети.
Пример 8. Ученику требуется купить учебник. Составить блок-схему, описывающую действия ученика в случае, если учебника нет в ряде магазинов.
Решение. Действия ученика в данном примере очевидны: когда он приходит в первый и любой последующий магазины, то возможны два варианта – учебник имеется в наличии или учебника нет в продаже. Если учебника нет в продаже, то ученику следует пойти в другой книжный магазин и спросить данный учебник, и т.д. пока учебник не будет куплен, т.к. перед учеником стоит конечная цель – купить учебник. Мы будем использовать цикл с предусловием, т.к. сначала требуется найти магазин, имеющий в наличии данный учебник. Цикл будет выполняться, пока условие “В данном магазине нет учебника” будет верным, а выход из цикла осуществится, когда условие станет ложным, т.е. когда ученик придет в магазин, в котором есть данный учебник. Действительно, в этом случае ученик купит нужный ему учебник и не будет больше искать книжные магазины. Результат блок-схемы представлен на рис. 2.12.
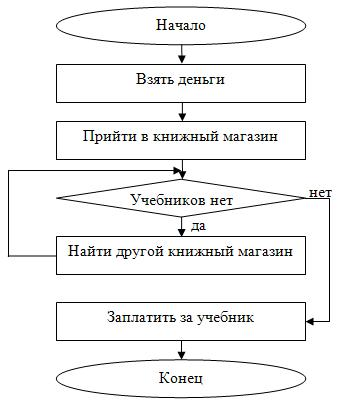
Рис.
2.12.
Блок-схема для примера 8
Здесь тело цикла состоит из одного действия “Найти другой книжный магазин”. Переменной цикла в явном виде нет, но можно подразумевать номер магазина, в который пришел ученик в очередной раз. Как любой другой цикл с предусловием, данный цикл может ни разу не выполниться (не иметь итераций), если в первом же магазине окажется нужный учебник.
Примечание. Если в данную задачу добавить условие выбора учебника в жесткой или мягкой обложке, как в примере 5, то оно появится после выхода из цикла. На реализацию циклического алгоритма данное условие не повлияет.
Пример 9. Даны числа . Известно, что число меняется от -10 до 10 с шагом 5, и не изменяется. Вычислить сумму и разность чисел и для всех значений и .
Решение. В отличие от примеров 3 и 6 здесь число меняется от -10 до 10 с шагом 5. Это означает, что число является переменной цикла. Сначала равно -10 – это первоначальное задание переменной цикла. Далее будет изменяться с шагом 5, и т.д. пока не будет достигнуто значение 10 – это соответствует изменению переменной цикла. Итерации надо повторять, пока выполняется условие “”. Итак, будет принимать следующие значения: -10, -5, 0, 5, 10. Число не будет являться переменной цикла, т.к. и не изменяется по условию задачи. Результат блок-схемы (с предусловием) представлен на рис. 2.13.
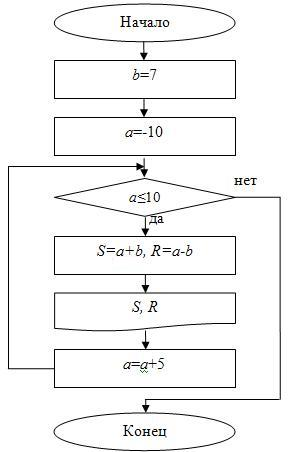
Рис.
2.13.
Блок-схема для примера 9 (с предусловием)
Тело цикла состоит из нескольких действий: вычисление суммы, вычисление разности и вывод полученных данных на экран. Таким образом, у нас получится несколько значений сумм и разностей, т.к. изменяется. Количество сумм и количество разностей совпадет с количеством различных значений , т.е. пять.
Данная задача может быть сделана и с циклом с предусловием, и с постусловием. В этом случае тело цикла, условие и изменение переменной цикла будут такими же, как и в цикле с предусловием, но сначала необходимо выполнить тело цикла, а потом проверить условие для выполнения следующей итерации.
Приведем блок-схему, использующую цикл с постусловием, на рис. 2.14.
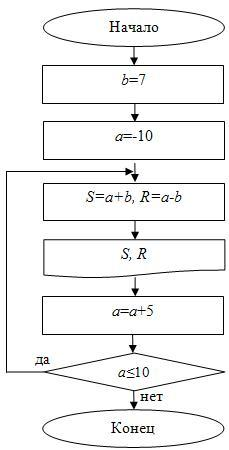
Рис.
2.14.
Блок-схема для примера 9 (с постусловием)
В данной задаче также могут быть соединены циклический и разветвляющийся алгоритмы, если по условию задачи требуется сравнить полученные значения суммы и разности, как в примере 6. В этом случае цикл можно реализовать как с предусловием, так и с постусловием, а сравнение суммы и разности добавится внутрь тела цикла, т.к. следует сравнить между собой все полученные суммы и разности. Организация самого цикла останется прежней. Приведем на рис. 2.15а блок-схему с предусловием, а на рис. 2.15б блок-схему с постусловием.
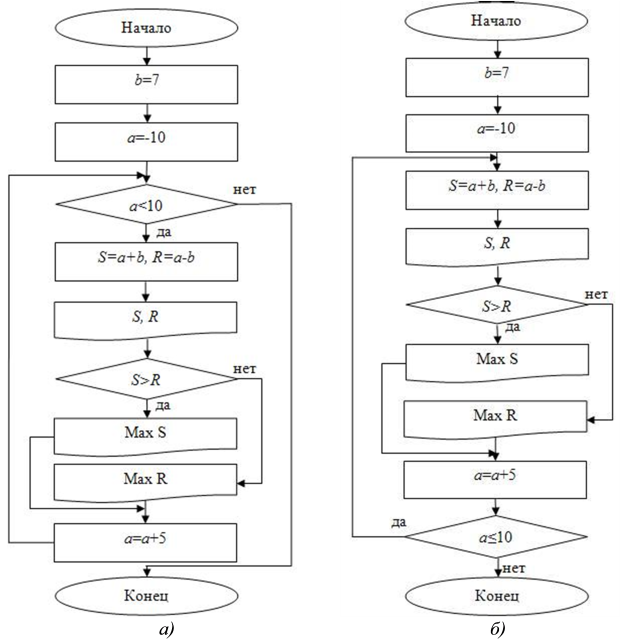
Рис.
2.15.
Блок-схема с ветвлением для примера 9: а) с предусловием, б) с постусловием
Источник
Программирование циклов
Рассмотрим приемы программирования циклов на Паскале. На уроках 33 – 35 “Программирование линейных алгоритмов” рассказывалось о том, что существуют две циклические алгоритмические структуры: цикл с предусловием (цикл-пока) и цикл с постусловием (цикл-до). Были показаны способы описания циклических структур в блок-схемах и на Алгоритмическом языке. Форматы соответствующих операторов цикла в Паскале следующие.
Цикл с предусловием (цикл-пока):
While < логическое выражение > Do
< оператор >
Цикл с постусловием (цикл-до):
Repeat
< оператор >
Until < логическое выражение >
Различают циклы с заданным числом повторений и итерационные циклы.
На примерах конкретных задач рассмотрим приемы программирования циклов.
В математике известно, что сумма следующего бесконечного числового ряда:
в пределе стремится к значению константы е = 2,71828182… Функция ех называется экспонентой, а логарифм по основанию е называется натуральным логарифмом: 1пх.
Требуется составить программу, вычисляющую эту константу по сумме числового ряда. Напомним, что символ «!» читается как «факториал» — функция, определенная следующим образом:
Если слагаемые в вычисляемом выражении обозначить так:
то обобщенная формула для i-го элемента будет следующей:
Нетрудно увидеть, что между элементами данной последовательности имеется зависимость:
Такая зависимость называется рекуррентной зависимостью, а соответствующая числовая последовательность — рекуррентной последовательностью. Данная рекуррентная последовательность может быть описана следующей ветвящейся формулой, которая называется рекуррентной формулой:
Циклы с заданным числом повторений
Пример 1. Дано целое положительное значение N. Требуется вычислить сумму:
Ниже приводятся два варианта программы решения этой задачи. В первом варианте используется цикл с предусловием, во втором — цикл с постусловием.

Обратите внимание на то, как цикл с предусловием преобразуется в цикл с постусловием — условие цикла помещается после тела цикла и заменяется на противоположное:
Not(i ≤ N) = i > N.
И тот, и другой цикл повторят свое выполнение (N + 1) раз. Переменная i выполняет роль не только знаменателя в дроби 1/i!, но и является счетчиком числа повторений цикла. Такие переменные называются параметрами цикла. И еще: в цикле с постусловием служебные слова Repeat и Until сами выполняют роль операторных скобок. Поэтому писать Begin и End здесь не требуется.
Выполнение этих программ на компьютере для значения N = 7 приводит к следующему результату: Е=2,7182539.
Для программирования циклов с заданным числом повторений при постоянном шаге изменения параметра цикла в Паскале существует цикл с параметром. Вот как выглядит программа решения той же задачи с использованием цикла с параметром:

В программе используется оператор цикла For, для которого существуют два варианта:
1) For <параметр цикла>:=<выражение 1> То <выражение 2>
Do <оператор>
2) For <параметр цикла>:=<выражение 1> Downto <выражение 2>
Do <оператор>
Здесь <параметр цикла> — имя простой переменной порядкового типа. Выполнение оператора For в первом варианте (То) происходит по следующей схеме.
1. Вычисляются значения <выражения 1> и <выражения 2>. Это делается только один раз при входе в цикл.
2. Параметру цикла присваивается значение <выражения 1>.
3. Значение параметра цикла сравнивается со значением <выражения 2>. Если параметр цикла меньше или равен этому значению, то выполняется тело цикла (<оператор>), в противном случае выполнение цикла заканчивается.
4. Значение параметра цикла изменяется на следующее значение в его типе (для целых чисел — увеличивается на единицу); происходит возврат к пункту 3.
Оператор цикла For объединяет в себе действия, которые при использовании цикла While выполняют различные операторы: присваивание параметру начального значения, сравнение его с конечным значением, изменение значения параметра на следующее.
Во втором варианте оператора For слово Downto буквально можно перевести как «вниз до». В таком случае параметр цикла изменяется по убыванию, т. е. при каждом повторении цикла параметр изменяет свое значение на предыдущее (равносильно i : =pred (i)).
Работая с оператором For, учитывайте следующие правила:
• параметр цикла не может иметь вещественного типа;
• в теле цикла нельзя изменять переменную-параметр цикла;
• при выходе из цикла значение переменной-параметра является неопределенным.
Рассмотрим пример программы, в которой в теле цикла будет присутствовать ветвление.
Пример 2. Составим программу проверки знаний учеником таблицы умножения. Компьютер задает ученику 10 вопросов на умножение чисел от 2 до 9. На каждое задание ученик вводит свой ответ, компьютер сообщает, верный ответ или нет.
На рисунке 3.16 приведена блок-схема такого алгоритма.
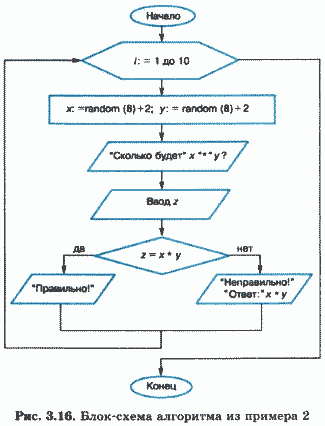
Обратите внимание на то, как отображается на блок-схеме цикл с параметром.
В этом алгоритме использована функция random (х), результатом выполнения которой является случайное целое число из диапазона от 0 до х – 1. Следовательно, выражение random (8)+2 принимает случайные значения от 2 до 9. Функция random называется датчиком случайных чисел.
На Паскале этот алгоритм программируется так:

А вот фрагмент интерфейса исполнения этой программы:
Сколько будет 4*8?
21
Неправильно! 4*8=32
Сколько будет 6*9?
54
Правильно!
В программе используется стандартная процедура randomize. Ее исполнение производит установку случайного начального состояния датчика случайных чисел. Благодаря этому при повторном выполнении программы будут получаться разные последовательности случайных чисел.
Вопросы и задания
1. Постройте трассировочную таблицу выполнения программы Summa_1 для значения n = 3.
2. Составьте программу, по которой компьютер десять раз запросит ввод любых чисел и в результате выведет среднее арифметическое значение введенных чисел (массив не использовать). Сделайте три варианта программы, используя операторы цикла While, Repeat и For.
3. Составьте программу, по которой компьютер десять раз запросит ввод целых чисел и в результате сообщит, сколько среди введенных чисел четных и сколько нечетных.
4. Составьте программу, по которой на экран будет выведена вся таблица умножения.
5. Усовершенствуйте программу TablMul (пример 2 данного параграфа) таким образом, чтобы в результате выводилось сообщение о количестве правильных и неправильных ответов.
6. Усовершенствуйте программу TablMul таким образом, чтобы в результате выводилась оценка, поставленная ученику. Критерии для выставления оценок придумайте сами.
7. Получите таблицу значений функции sin x и cos x на отрезке [0, 1] с шагом 0,1 в следующем виде:
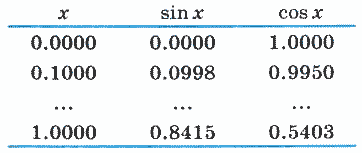
8. Получите в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр.
9. Значение функции е х (экспонента от х) равно сходящейся сумме бесконечного ряда:
Получите рекуррентную формулу для слагаемых. Используя операторы цикла While, Repeat и For, составьте три варианта программы вычисления суммы с заданным числом слагаемых.
Вложенные и итерационные циклы
Если в теле одного цикла имеется другой цикл, то такая структура алгоритма называется вложенными циклами. Рассмотрим задачу, программа решения которой имеет структуру вложенных циклов.
Требуется получить на экране компьютера таблицу умножения в форме матрицы Пифагора. Блок-схема алгоритма будет следующей (рис. 3.17).
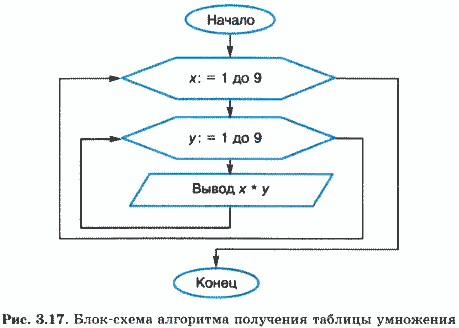
Здесь цикл по параметру у вложен в цикл по параметру х. Последовательность изменения значений параметров циклов такая:
х = 1; у = 1, 2, 3, …, 9
х = 2; у = 1, 2, 3, …, 9
…
х = 9; у = 1, 2, 3, …, 9
Таким образом, внешний цикл исполнится 9 раз, а внутренний — 9 • 9 = 81 раз. На один шаг повторения внешнего цикла происходит полная прокрутка внутреннего.
При программировании вложенных циклов используется понятие глубины вложенности. В данном примере глубина вложенности внутреннего цикла равна единице. Если бы внутри вложенного цикла был еще один вложенный цикл (например, для вычисления всех вариантов перемножения трех сомножителей), то его глубина вложенности равнялась бы двум.
Программа на Паскале получения матрицы Пифагора:

В результате выполнения программы на экране получим:
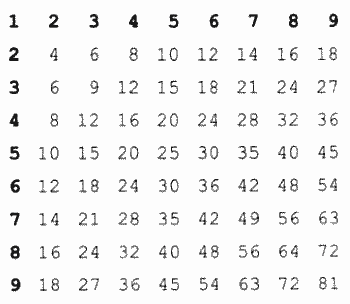
В программе присутствуют некоторые элементы, не отраженные в блок-схеме. В описании переменных X, Y использован ограниченный тип: 1. . 9, поскольку в данной задаче величины принимают целые значения только в этом диапазоне. Оператор WriteLn перед началом вложенного цикла обеспечивает переход к новой строке в таблице каждый раз при смене первого сомножителя. В операторе Write(X*Y:3) для вывода значения произведения после двоеточия использован указатель формата — 3. Это обеспечивает вывод чисел в три позиции на экране, благодаря чему соответствующие столбцы таблицы располагаются строго друг под другом. Первая строка и первый столбец на экране — это сомножители, что соответствует стандартному формату таблицы Пифагора.
Итерационные циклы
Итерационный цикл — это цикл, для которого число повторений тела цикла заранее неизвестно. В итерационных циклах на каждом шаге вычислений происходят последовательное приближение и проверка условия достижения искомого результата. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.
Пример 1. Снова рассмотрим задачу вычисления суммы числового ряда:
Но теперь условие будет таким: в сумму нужно включить только слагаемые, значение которых больше некоторой малой величины ε. При этом полученная сумма будет отличаться от предельного значения (константы е) на величину, не большую ε.
Поскольку с увеличением значения i величина 1/i! уменьшается, в сумму надо включать все слагаемые, предшествующие первому значению, меньшему ε. Вот две программы решения этой задачи, использующие циклы с предусловием и постусловием:

Решить эту задачу, используя цикл с параметром, нельзя. Итерационные циклы программируются путем использования либо цикла-пока, либо цикла-до.
В качестве результата выводится значение суммы и число вошедших в нее слагаемых. Выполнение этих программ для значения ε=10 -8 дает в результате: Е=2,71828182, Слагаемых: 12. Таким образом, за 12 повторений цикла значение константы е получено с точностью до 8 знаков после запятой. Слово «итерации» означает «приближения». С каждым повторением цикла вычисляемая величина приближалась к предельному значению константы.
Пример 2. На уроках 33 – 35 “Программирование линейных алгоритмов” была рассмотрена задача вычисления суммы цифр трехзначного натурального числа. Программа имела линейную структуру. Поставим задачу в более общем виде: для любого многозначного натурального числа вычислить сумму всех его цифр.
Выделение цифр происходит с помощью однотипных действий: использования операций mod и div. Очевидно, что их можно «зациклить». Однако число повторений цикла будет разным для чисел разной длины. Поэтому эта задача не решается с помощью цикла с заданным числом повторений. В таком случае в программе можно использовать либо оператор цикла While, либо Repeat и нельзя — цикл с параметром For.
Программа с использованием цикла с предусловием:

Поскольку при каждом повторении цикла от числа X отбрасывается одна младшая цифра, закончить цикл нужно тогда, когда X станет равным нулю. Обратите внимание на типы переменных. Надо помнить о разнообразии групп типов в Паскале. Назначение переменной X типа Longint дает возможность вводить в нее значения, включающие до десяти знаков. Для переменной Sum, назначен тип Word, поскольку сумма цифр может быть только положительным числом.

Вопросы и задания
1. Найдите все значения натуральных чисел X, Y, Z из интервала от 1 до 10, удовлетворяющих равенству: X2 + Y2 = Z2.
2. Вычислите количество точек с целочисленными координатами, попадающих в круг радиуса R (R > 0) с центром в начале координат.
3. Старинная задача. Сколько можно купить быков, коров и телят на 100 руб., если в сумме должно быть куплено 100 голов скота, а цена быка — 10 руб., цена коровы — 5 руб., цена теленка — 0,5 руб.?
4. Чем отличается итерационный цикл от цикла с заданным числом повторений?
5. Почему для программирования итерационных циклов не используется оператор цикла с параметром?
6. Запрограммируйте итерационный цикл вычисления функции е х (см. задание 9 из “Программирование циклов”*1*) с точностью ε. Сделайте два варианта программы: с циклами While и Repeat. Выполните вычисления для ε = 10
-6, х = 2 и сопоставьте полученный результат со значением стандартной функции ехр (х).
7. Составьте программу определения количества четных и нечетных цифр в записи данного натурального числа.
8. Составьте программу определения наибольшей цифры в записи данного натурального числа.
*1*Задание 9 из “Программирование циклов”
Значение функции е х (экспонента от х) равно сходящейся сумме бесконечного ряда:
Получите рекуррентную формулу для слагаемых. Используя операторы цикла While, Repeat и For, составьте три варианта программы вычисления суммы с заданным числом слагаемых.
Практикум
Работа 3.4. Программирование циклических алгоритмов
Задание 1
Циклы с заданным числом повторений
Вычислить значение суммы или произведения числовой последовательности.
Уровень 1
1. Дано натуральное число N. Вычислить:
2. Дано натуральное число N. Вычислить:
3. Дано натуральное число N. Вычислить:
4. Дано натуральное число N. Вычислить:
5. Дано натуральное число N. Вычислить произведение первых N сомножителей:
6. Дано натуральное n. Вычислить:
7. Вычислить:
Уровень 2
8. Дано натуральное число N. Вычислить:
9. Дано действительное число х. Вычислить:
10. Даны натуральное n, действительное х. Вычислить:
11. Дано действительное х. Вычислить:
12. Дано натуральное n. Вычислить:
13. Дано натуральное число n. Вычислить:
14. Вычислить по схеме Горнера:
15. Числа Фибоначчи (f n ) определяются формулами
Для данного значения р определить f p .
16. Даны натуральные числа n и k. Вычислить:
Задание 2
Итерационные циклы
Найти наименьший номер последовательности, заданной рекуррентной формулой, для которого выполняется условие |аn – аn-1| < ε, где ε — малая величина. Вывести на экран этот номер и все элементы ai, где
i = 1, 2, …, n.
Задание 3
Циклы при обработке целых чисел
Решить поставленные задачи с помощью циклических алгоритмов (простых и вложенных), используя операции целочисленной арифметики.
Уровень 2
1. Натуральные числа а, b, с называются числами Пифагора, если выполняется условие а2 + b2 = с2. Напеча