Вычислить факториал в цикле
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал – быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Наивный алгоритм
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
ic BigInteger FactNaive(int n) { BigInteger r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; }
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
Реализуем описанный алгоритм:
ic BigInteger ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r – l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } ic BigInteger FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); }
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K2-ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K2. Аналогично для K3, K4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K2 + N / K3 + N / K4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (22), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (23), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (24) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 28 * 34 * 52 * 71 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
ic BigInteger FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; bool[] u = new bool[n + 1]; // маркеры для решета Эратосфена List<Tuple<int, int>> p = new List<Tuple<int, int>>(); // множители и их показатели степеней for (int i = 2; i <= n; ++i) if (!u[i]) // если i – очередное простое число { // считаем показатель степени в разложении int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } // запоминаем множитель и его показатель степени p.Add(new Tuple<int, int>(i, c)); // просеиваем составные числа через решето int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } // вычисляем факториал BigInteger r = 1; for (int i = p.Count() – 1; i >= 0; –i) r *= BigInteger.Pow(p[i].Item1, p[i].Item2); return r; }
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Библиотека GMP
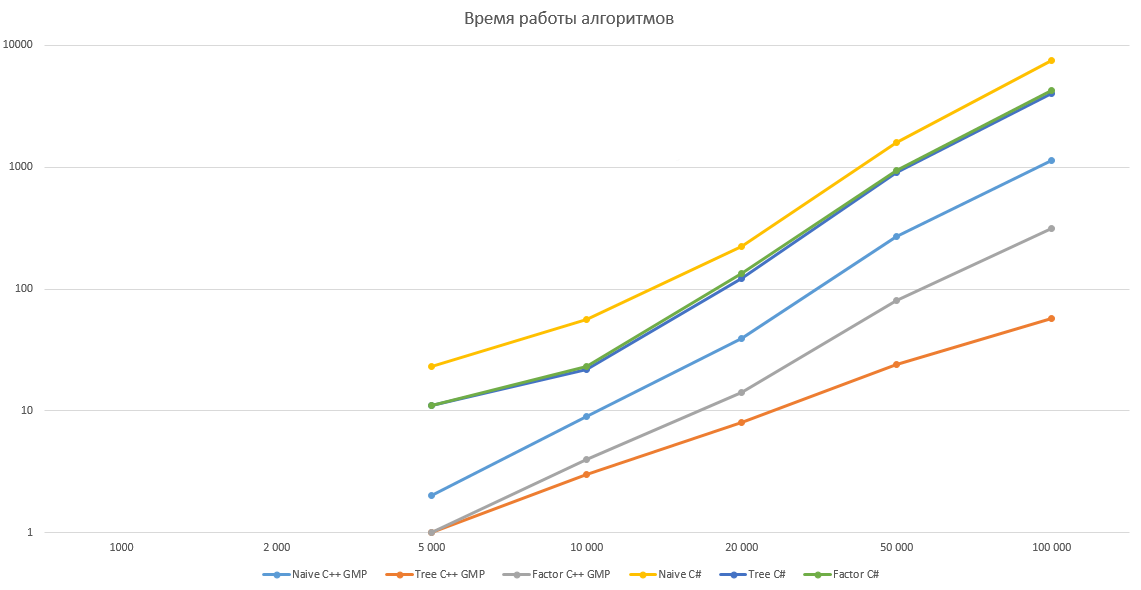
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
Сравнение производительности
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
График с линейной шкалой
График с логарифмической шкалой
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
lany распараллелил дерево на Java с помощью Stream API и получил ускорение в 18 раз
Mrrl предложил оптимизацию факторизации на 15-20%
PsyHaSTe предложил улучшение наивной реализации
Krypt предложил распараллеленную версию на C#
SemenovVV предложил реализацию на Go
pomme предложил использовать GMP
ShashkovS предложил быстрый алгоритм на Python
Исходные коды
Исходные коды реализованных алгоритмов приведены под спойлерами
C#
using System; using System.Linq; using System.Text; using System.Numerics; using System.Collections.Generic; using System.Collections.Specialized; namespace BigInt { class Program { ic BigInteger FactNaive(int n) { BigInteger r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; } ic BigInteger ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r – l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } ic BigInteger FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); } ic BigInteger FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; bool[] u = new bool[n + 1]; List<Tuple<int, int>> p = new List<Tuple<int, int>>(); for (int i = 2; i <= n; ++i) if (!u[i]) { int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } p.Add(new Tuple<int, int>(i, c)); int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } BigInteger r = 1; for (int i = p.Count() – 1; i >= 0; –i) r *= BigInteger.Pow(p[i].Item1, p[i].Item2); return r; } ic void Main(string[] args) { int n; int t; Console.Write(“n = “); n = Convert.ToInt32(Console.ReadLine()); t = Environment.TickCount; BigInteger fn = FactNaive(n); Console.WriteLine(“Naive : {0} ms”, Environment.TickCount – t); t = Environment.TickCount; BigInteger ft = FactTree(n); Console.WriteLine(“Tree : {0} ms”, Environment.TickCount – t); t = Environment.TickCount; BigInteger ff = FactFactor(n); Console.WriteLine(“Factor : {0} ms”, Environment.TickCount – t); Console.WriteLine(“Check: {0}”, fn == ft && ft == ff ? “ok” : “fail”); } } }
C++ с GMP
#include <iostream> #include <c> #include <vector> #include <utility> #include <gmpxx.h> using namespace std; mpz_class FactNaive(int n) { mpz_class r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; } mpz_class ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r – l == 1) return (mpz_class)r * l; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } mpz_class FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); } mpz_class FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; vector<bool> u(n + 1, false); vector<pair<int, int> > p; for (int i = 2; i <= n; ++i) if (!u[i]) { int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } p.push_back(make_pair(i, c)); int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } mpz_class r = 1; for (int i = p.size() – 1; i >= 0; –i) { mpz_class w; mpz_pow_ui(w.get_mpz_t(), mpz_class(p[i].first).get_mpz_t(), p[i].second); r *= w; } return r; } mpz_class FactNative(int n) { mpz_class r; mpz_fac_ui(r.get_mpz_t(), n); return r; } int main() { int n; uned int t; cout << “n = “; cin >> n; t = (); mpz_class fn = FactNaive(n); cout << “Naive: ” << (() – t) * 1000 / S_PER_SEC << ” ms” << endl; t = (); mpz_class ft = FactTree(n); cout << “Tree: ” << (() – t) * 1000 / S_PER_SEC << ” ms” << endl; t = (); mpz_class ff = FactFactor(n); cout << “Factor: ” << (() – t) * 1000 / S_PER_SEC << ” ms” << endl; t = (); mpz_class fz = FactNative(n); cout << “Native: ” << (() – t) * 1000 / S_PER_SEC << ” ms” << endl; cout << “Check: ” << (fn == ft && ft == ff && ff == fz ? “ok” : “fail”) << endl; return 0; }
Источник
Как вычислить факториал в Python?
Считать факториал легко, если вам помогает питоновская программа, щелкающая математические операции, как орешки. Однако, прежде, чем Python порадует нас правильными рассчетами, придется нам порадовать Питона новой порцией отменного кода под названием «Факториал!». Но, сначала краткий математический ликбез:
Что такое факториал числа?
Факториалом числа N называется произведение всех чисел от единицы до N. О том, что речь идет о факториале, «говорит» восклицательный знак после числа N.
Например, факториал 5 считается так: 5! = 1*2*3*4*5
А факториал 12 равен: 12! = 1*2*3*4*5*6*7*8*9*10*11*12.
Кстати, факториал нуля равен единице, как и факториал самой единицы: 0! = 1 1! = 1
Это нужно запомнить, и обязательно закодить в своей программе!
Пишем код на Python для вычисления факториала
Внимание! При написании кода необходимо учесть, что нельзя вычислить факториал нецелого или отрицательного числа. Поэтому необходимо добавить соответствующую проверку!
Рассмотрим несколько вариантов написания кода:
1. Cамый простой вариант. Это будет цикл for, принимающий на вход число n и выводящий в ответ посчитанный факториал. Если число n является нецелым или отрицательным, выведем сообщение об ощибке. В качестве тренировки, после него рекомендую усложнить задачу и заключить цикл в функцию, как во втором варианте.
2. Вариант – это функция для вычисления факториала, которой в качестве аргумента будем передавать число n. Этот вариант является «причесанным» первым вариантом.
3. Вариант – это облагороженный 2-й вариант. Помимо того, что вычисление факториала будет производиться при вызове функции, так еще и программа любезно «попросит» пользователя ввести число, факториал которого нужно рассчитать.
Итак, приступим к реализации задуманных вариантов!
ВАРИАНТ №1: Пишем цикл for для вычисления факториала в Python!
Предлагаю сначала взглянуть на рабочий код. Позже мы рассмотрим каждый шаг подробно:
# число, факториал которого нужно вычислить num = 5 # начальное значение факториала factorial = 1 # Если num является натуральным, то if(num%1==0 and num>=0): # Вычисляем факториал числа num for i in range(1, num+1): factorial = i*factorial # Выводим результат на экран (f'{num}! = {factorial}’) # Если num – отрицательное или нецелое число, выводим сообщение об ошибке else: (‘Невозможно вычислить факториал нецелого и/или отрицательного числа!’)
При значении num=5, результат работы кода выглядит следующим образом:
5! = 120
А при нецелом значении 3.2:
Невозможно вычислить факториал нецелого и/или отрицательного числа!
Разберем код варианта №1 подробно:
1. Объявляем переменную num и передаем ей число, факториал которого требуется найти:
# число, факториал которого нужно вычислить num = 5
2. Определяем переменную factorial, в которой будет храниться значение вычисленного факториала. В качестве начального значения устанавливаем «1»
# число, факториал которого нужно вычислить num = 5 # начальное значение факториала factorial = 1
3. Проверяем, верно ли задано значение переменной num. Если пользователь ввел нецелое число, тогда остаток от деления этого нецелого числа на единицу будет больше нуля.
Операция «%» в Python позволяет получить остаток от деления первого числа на второе. Например, 5%1 =0, а 5.5%1 = 0.5
Таким образом, чтобы проверить, является ли num, целым, нужно сравнить результат операции num%1 с нулем. Кроме этого, нужно убедиться, что число num не является отрицательным, для этого проверим выполнение неравенства num >= 0:
Добавим проверку перечисленных выше условий:
# число, факториал которого нужно вычислить num = 5 # начальное значение факториала factorial = 1 if (num%1==0 and num>=0): # здесь будем считать факториал #Если же num не удовлетворяет перечисленным условиям, выведем сообщение об ошибке: else: (‘Невозможно вычислить факториал нецелого и/или отрицательного числа!’)
4. Вычислим значение факториала числа num. Для целого числа i, принимающего целые значения от 1(включительно) до n+1(не включительно), будем вычислять текущее значение факториала на i и присваивать факториалу новое полученное значение. То есть, при расчете 4! будут происходить действия:
при i=1 factorial = 1*1=1 при i=2 factorial = 2*1 = 2 при i =3 factorial = 3*2 = 6 при i =4 factorial = 4*6 = 24 # число, факториал которого нужно вычислить num = 5 # начальное значение факториала factorial = 1 if (num%1==0 and num>=0): for i in range(1, num+1): factorial = i*factorial #Если же num не удовлетворяет перечисленным условиям, выведем сообщение об ошибке: else: (‘Невозможно вычислить факториал нецелого и/или отрицательного числа!’)
5. Вывод результата на экран осуществим в виде строки:
(f'{num}! = {factorial}’)
Такая конструкция (с буквой f перед кавычками) позволяет вывести значение переменной, заключенной в фигурные скобки. В итоге, код приобретет вид:
# число, факториал которого нужно вычислить num = 5 # начальное значение факториала factorial = 1 # Если num является натуральным, то if(num%1==0 and num>=0): # Вычисляем факториал числа num for i in range(1, num+1): factorial = i*factorial # Выводим результат на экран (f'{num}! = {factorial}’) # Если num – отрицательное или нецелое число, выводим сообщение об ошибке else: (‘Невозможно вычислить факториал нецелого и/или отрицательного числа!’)
ВАРИАНТ №2: Создаем функцию для вычисления факториала!
1. Для начала объявим функцию find_factorial(num), которая в качестве аргумента будет принимать число, факториал которого требуется вычислить:
2. Определяем переменную для хранения текущего значения факториала, присваиваем ей значение «1»:
def find_factorial(num): # определяем начальное значение факториала factorial=1
3. Затем, весь написанный в «Варианте №1» код, начиная с проверки на корректность переменной num, помещаем в функцию find_factorial(num). При этом нужно заменить «» на «return», так как функция ничего не будет выводить на экран, а будет возвращать полученное значение факториала или сообщение об ошибке:
def find_factorial(num): # определяем начальное значение факториала factorial=1 # Если num является натуральным, то if(num%1==0 and num >= 0): # Вычисляем факториал числа num for i in range(1, num+1): factorial = i*factorial return (f'{num}! = {factorial}’) else: return (‘Невозможно вычислить факториал нецелого и/или отрицательного числа!’)
Если какой-то момент в коде для Вас не понятен, перечитайте внимательно приведенный выше детальный разбор кода в «Варианте 1»
4. Осталось только вызвать нашу новую функцию и проверить, корректно ли она работает. Для этого определим число, факториал которого будем считать. Затем вызовем функцию find_factorial() для вычисления факториала числа num. Полученный от функции ответ сохраним в переменной factorial и выведем эту переменную на экран:
def find_factorial(num): # определяем начальное значение факториала factorial=1 # Если num является натуральным, то if(num%1==0 and num >= 0): # Вычисляем факториал числа num for i in range(1, num+1): factorial = i*factorial return (f'{num}! = {factorial}’) else: return (‘Невозможно вычислить факториал нецелого и/или отрицательного числа!’) # Определим число, факториал которого будем считать num = 6 # Вызовем функцию find_factorial() для вычисления факториала factorial = find_factorial(num) # Выведем полученный от функции ответ на экран (factorial)
Наша функция отлично работает и может стать полезным ингредиентом в самописной библиотеке для математических вычислений! Однако, мы можем украсить наш код небольшой изюминкой, чем и займемся при рассмотрении «Варианта №3».
ВАРИАНТ №3: Облагородим код, вычисляющий факториал в Python, строкой пользовательского ввода.
Давайте добавим скрипту интерактивности – вежливо попросим пользователя ввести число, факториал которого нужно вычислить. Затем, после ввода числа и нажатия пользователем клавиши «Enter», обратимся к функции find_factorial() и выведем результат на экран. Для этого требуется лишь заменить строку, в которой мы задавали значение переменной num, следующей строкой:
num = eval(input(“Факториал какого числа считаем? “))
Функция input() в Python3 позволяет получить введенную пользователем информацию.
Функция eval() позвляет динамически обновить данные.
В итоге, обновленный работающий код будет выглядеть так:
def find_factorial(num): # определяем начальное значение факториала factorial=1 # Если num является натуральным, то if(num%1==0 and num >= 0): # Вычисляем факториал числа num for i in range(1, num+1): factorial = i*factorial return (f'{num}! = {factorial}’) else: return (‘Невозможно вычислить факториал нецелого и/или отрицательного числа!’) # Ввод числа, факториал которого будем считать num = eval(input(“Факториал какого числа считаем? “)) # Вызовем функцию find_factorial() для вычисления факториала factorial = find_factorial(num) # Выведем полученный от функции ответ на экран (factorial)
Мы рассмотрели 3 варианта, от самого простого, до самого «облагороженного», которые можно использовать для решения задачи по вычислению факториала в Python. Несмотря на то, что эта задача является довольно простой, она отлично подходит для тренировки навыков программирования в Python!
Источник
Введение
Вычисление факториала – одна из традиционных программистских задач для собеседований. Если вдруг кто забыл, факториал натурального числа N обозначается как N! и равняется произведению всех натуральных чисел от единицы до N включительно. Например, . Казалось бы, что тут сложного? Однако есть свои нюансы.
Например, сравним два самых распространённых способа вычисления факториала.
Через цикл
factorial(n){ var result = 1; while(n){ result *= n–; } return result; }
Через рекурсию
factorial(n, result){ result = result || 1; if(!n){ return result; }else{ return factorial(n-1, result*n); } }
Многие скажут, что первый способ лучше, но это не так. Во-первых, циклы уже не в тренде, сейчас модно функциональное программирование. Во-вторых, чем больше людей используют второй способ, тем быстрее в основных джаваскриптовых движках появится оптимизация хвостовой рекурсии.
В любом случае, оба эти способа слишком примитивны, чтобы по ним судить о знаниях кандидата. А вот опытный разработчик на React.js уже может написать что-то в этом роде:
var React = require(“react”); var Factorial = React.createClass({ render: (){ var result = this.props.result || 1, n = this.props.n; if(!n){ return <span>{result}</span> }else{ return <Factorial n={n – 1} result={result*n}/> } } }); module.exports = Factorial;
Согласитесь, выглядит гораздо солиднее. Впрочем, невооружённым глазом видно, что это всего лишь вариант рекурсивного вычисления. Сходство станет ещё сильнее, если переписать Factorial как функциональный компонент. И, разумеется, я не стал бы писать этот хабрапост, если бы не был готов предложить нечто принципиально новое.
Начнём издалека
Какую из возможностей Javascript недолюбливают и недооценивают сильнее всего? Недолюбливают настолько, что про неё даже придумали специальную поговорку? Конечно же, это eval. Можно сказать, что eval – это тёмная сторона Силы. А как мы помним из фильмов Джорджа Лукаса, нет ничего более крутого и впечатляющего, чем тёмная сторона Силы, поэтому давайте попробуем ей овладеть.
Можно было бы запихнуть в строку какой-нибудь из методов, приведённых в начале поста, а затем передать эту строку в eval, но в этом не было бы новизны. Поставим задачу таким образом, чтобы сделать этот хак невозможным. Пусть у нас есть такой вот каркас:
factorial(n){ var f = “это единственное место в коде, которое мы имеем право изменить”; f = f.replace(“$”, n); for(let i = 0; i < n; i++){ if(parseInt(f)){ throw new Error(“Cheaters are not allowed”); } f = eval(f); } return parseInt(f); }
– и мы хотим, внеся изменения лишь в литерал строки f, сделать так, чтобы функция factorial взаправду вычисляла факториал. Вот задача, достойная истинного ситха.
Что-то это напоминает
Нам нужен код, который возвращает код, который возвращает код… Если забыть про конечную задачу – вычисление факториала, то есть одна хорошо известная штука, которая нам подойдёт. Эта штука называется квайн – программа, которая выводит свой собственный текст.
Про квайны на Хабре написано уже немало, потому я напомню лишь основные принципы квайностроительства. Чтобы сделать простейший квайн, нам нужно:
- Задать строку, которая содержит весь остальной текст программы.
- Подставить в эту строку её же саму
- Позаботиться об экранировании символов и прочих мелочах
- Вывести получившуюся строку
- ???
- PROFIT
Вооружившись этим знанием, можно написать следующий квайн на js (отступы и переносы строки добавлены для удобства читателя):
var o = { q: ”’, b: ‘\’, s: ‘var o = {q: _q_b_q_q, b:_q_b_b_q, s: _q_s_q}; console.log(Object.keys(o).reduce((a, k){return a.split(_q__q + k).join(o[k])}, o.s))’ }; console.log(Object.keys(o).reduce((a, k){return a.split(‘_’ + k).join(o[k])}, o.s));
В строке o.s содержится весь остальной код, а также специальные подстановочные последовательности, начинающиеся с подчёркивания. Страшное выражение внутри console.log заменяет каждую подстановочную последовательность на соответствующее свойство объекта o, что обеспечивает выполнение пунктов 2 и 3 хитрого плана по созданию квайна.
Лирическое отступление
Здесь меня могут поправить: товарищ, это не простейший квайн, а монстр какой-то. Простейший квайн на js выглядит так:
! $(){console.log(‘!’+$+'()’)}()
Это правда, но не совсем. Такой квайн считается «читерским», поскольку он из тела функции получает доступ к её же тексту. Это почти то же самое, что прочитать с жёсткого диска файл с исходным кодом программы. Моветон, одним словом.
Скрещиваем ежа с ужом
Как же сделать так, чтобы наш квази-квайн модифицировал сам себя, а в результате превратился в одно-единственное число? Давайте забудем пока про вычисление факториала и постараемся просто написать строку, которая «схлопывается» через определённое количество eval’ов. Для этого нам понадобится:
- Некий счётчик
- Соответствующая ему подстановочная последовательность
- Место, где этот счётчик модифицируется
- Проверка того, завершён ли обратный отсчёт
Выглядеть это будет примерно так:
var f = “var o = {” + “q: ‘\”,” + “b: ‘\\’,” + “n: 10,” + “s: ‘var o = {q: _q_b_q_q, b:_q_b_b_q, n:_n, s: _q_s_q}; o.n–; ” + “o.n ? Object.keys(o).reduce((a, k){return a.split(_q__q + k).join(o[k])}, o.s) : 0;'” + “};” + “o.n–;” + “o.n ? Object.keys(o).reduce((a, k){return a.split(‘_’ + k).join(o[k])}, o.s) : 0;” for(let i = 0; i < 10; i++){ f = eval(f); console.log(f); }
Обратите внимание на отсутствие return внутри строки: в нём нет необходимости, eval возвращает значение последнего выражения. Запустив этот код в консоли, можно c благоговением наблюдать, как с каждой итерацией цикла значение n уменьшается на 1. Если кто-то скажет, что для такого эффекта достаточно:
f.replace(/n: ([0-9]+)/, (_, n) => “n: ” + (n – 1))
– то у него нет чувства прекрасного.
После этого подготовительного этапа уже совсем нетрудно написать итоговую версию вычисления факториала. Просто добавляется ещё одна переменная и чуть усложняется строчка с изменением.
factorial(n){ var f = “var o = {” + “q: ‘\”,” + “b: ‘\\’,” + “r: 1,” + “n: $,” + “s: ‘var o = {q: _q_b_q_q, b:_q_b_b_q, r: _r, n:_n, s: _q_s_q}; o.r *= o.n–; ” + “o.n ? Object.keys(o).reduce((a, k){return a.split(_q__q + k).join(o[k])}, o.s) : o.r;'” + “};” + “o.r *= o.n–;” + “o.n ? Object.keys(o).reduce((a, k){return a.split(‘_’ + k).join(o[k])}, o.s) : o.r;” f = f.replace(“$”, n); for(var i = 0; i < n; i++){ if(parseInt(f)){ throw new Error(“Cheaters are not allowed.”); } f = eval(f); } return parseInt(f); }
Теперь вы можете смело идти на собеседование.
Заключение
С живым кодом можно поиграться здесь. Как и в прошлой статье из рубрики «Пятничный JS» напоминаю: если вы сделаете что-нибудь подобное на продакшене, то попадёте в ад. С другой стороны, если вы сделаете это на собеседовании, то вам не дадут возможности сделать это на продакшене, и вы не попадёте в ад. Так что делайте это на собеседовании. Спасибо за внимание.
Источник