Второе начало термодинамики тепловая машина цикл карно
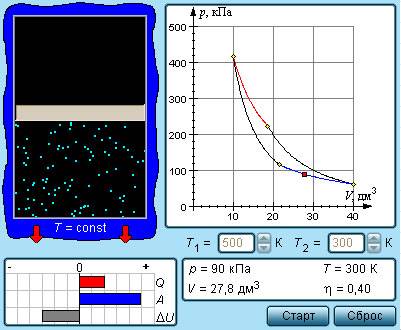
Тепловая машина – устройство, преобразующее тепловую энергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник). Преобразование осуществляется за счёт изменения внутренней энергии рабочего тела — на практике обычно пара или газа.
При работе часть тепла Q1 передается от нагревателя к рабочему телу, а затем часть энергии Q2 передается холодильнику, который охлаждает машину. КПД тепловой машины считается по формуле (Q1-Q2)/Q1)х100.
В термодинамике цикл Карно или процесс Карно — это обратимый круговой процесс, состоящий из двух адиабатическихи двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.
Пусть тепловая машина состоит из нагревателя с температурой Тн, холодильника с температурой Тх и рабочего тела.
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах T (температура) и S (энтропия).
1. Изотермическое расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру Тн, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Qн. При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника Тх, тело совершает механическую работу, а энтропия остаётся постоянной.
3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру Тх, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты Qх. Над телом совершается работа, его энтропия уменьшается.
4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
.
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
.
Отсюда коэффициент полезного действия тепловой машины Карно равен
.
Рис. 1. Цикл Карно в координатах T—S
Рис. 2. Цикл Карно в координатах P и V
Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.
Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния
называемая энтропией, такая, что ее полный дифференциал
Источник
Тепловые машины — устройства, в которых за счет внутренней энергии топлива совершается механическая работа. Чтобы тепловая машина работала циклически, необходимо, чтобы часть энергии, полученной от нагревателя, она отдавала холодильнику.
Второе начало термодинамики
В циклически действующем тепловом двигателе невозможно преобразовать все количество теплоты, полученное от нагревателя, в механическую работу.
В тепловых машинах тепловые процессы замыкаются в цикле Карно. Так называют цикл, или идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В цикле Карно термодинамическая система выполняет механическую работу за счет обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры.
На графике цикл Карно представляется как две адиабаты и две изотермы:
- 1–2 — изотермическое расширение;
- 2–3 — адиабатное расширение;
- 3–4 — изотермическое сжатие;
- 4–1 — адиабатное сжатие.
КПД тепловой машины
Максимальный КПД соответствует циклу Карно.
Второе начало термодинамики
η=Qн−QхQн100%=Qн−PхtQн100%
Преобразовывая формулу, получим:
η=A‘Qн100%
η=NtQн100%
η=A‘A‘+Qх100%
η=Tн−TхTн100%
- Qн (Дж) — количество теплоты, полученное от нагревателя (полученное количество теплоты);
- Qх (Дж) — количество теплоты, отданное холодильнику (отданное количество теплоты);
- A’ (Дж) — работа, совершенная газом;
- N (Вт) — полезная мощность;
- t (с) — время;
- Tн (К) — температура нагревателя;
- Tх (К) — температура холодильника.
Важно! Температуру следует выражать только в кельвинах (К) и КПД не бывает больше 100%.
Алгоритм решения задач на определение КПД теплового процесса
Рассмотрим решение на примере конкретной задачи:
На p-V-диаграмме изображен цикл, проводимый с одноатомным идеальным газом. Определите КПД этого цикла.
- Определить работу газа.
Если тепловой процесс представлен в осях (p, V), то можно определить работу, вычислив площадь фигуры, ограниченной замкнутым циклом:
A‘=p0V0
Если тепловой процесс представлен в других осях координат, то сначала следует его перестроить в осях (p, V) и только потом определять работу.
- Выяснить, на каких этапах повышается температура газа. Именно здесь газ получает энергию:
1–2: V = const, давление увеличивается, температура увеличивается.
2–3: p = const, объем увеличивается, температура увеличивается.
3–4: V = const, давление понижается, температура понижается.
4–1: p = const, объем уменьшается, температура уменьшается.
Отсюда следует, что газ получает энергию только на первом и втором этапах.
- Определить с помощью первого начала термодинамики количество теплоты, полученное газом:
1–2: V = const, A12’ = 0,
Q12=ΔU12=32ΔpV=32Δp0V0=1,5p0V0
1–2: p = const,
ΔU23=Q23−A23;
ΔU23=32ΔpV=322Δp0V0=3p0V0
A23=pΔV=2p0V0
Q23=3p0V0+2p0V0=5p0V0
Общее количество теплоты:
Qполуч=Q12+Q23=6,5p0V0
- Вычислить КПД, используя основную формулу:
η=A‘Qполуч100%
η=p0V06,5p0V0100%=15,4%
Ответ:
а) 1,2 кДж
б) 1,8 кДж
в) 2,6 кДж
г) 3,9 кДж
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Определить работу газа на заданном участке.
3.Выполнить решение в общем виде.
4.Выполнить вычисления, подставив известные данные.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу от нагревателя: Qнагр = 5,1 кДж.
• Масса постоянна: m = const.
5,1 кДж = 5,1∙103 Дж
Согласно графику, на участке 1–2 газ совершает работу, равную:
A=3p0(4V0−V0)=9p0V0
Полезная работа ограничивается площадью фигуры внутри циклического графика. Она равна:
Aползн=9p0V0−p0(4V0−V0)=6p0V0
Отсюда:
A=9Aползн6
КПД тепловой машины есть отношение полезной работы к количеству теплоты, полученному от нагревателя:
η=AползнQ
Отсюда:
Aползн=ηQ
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Температура нагревателя идеального теплового двигателя, работающего по циклу Карно, равна T1, а температура холодильника равна T2. За цикл двигатель получает от нагревателя количество теплоты Q1. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Определить, от чего зависит КПД двигателя. Выбрать верную формулу.
2.Определить, как вычисляется работа, совершаемая за цикл. Выбрать верную формулу.
Решение
КПД двигателя определяется отношением разности температур нагревателя и холодильника к температуре нагревателя:
η=T1−T2T1=1−T2T1
Верный ответ для «А» — 1.
Работа, совершаемая за цикл, определяется произведением КПД на количество теплоты, полученного от нагревателя:
A=Qη=Q(T1−T2T1)
Верный ответ для «Б» — 2.
Ответ: 12
pазбирался: Алиса Никитина | обсудить разбор | оценить
Рабочее тело идеальной тепловой машины с КПД, равным 0,25, за цикл своей работы получает от нагревателя количество теплоты, равное 8 Дж. Какова работа, совершаемая за цикл этой машиной?
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу КПД тепловой машины.
3.Записать решение в общем виде.
4.Выполнить вычисление искомой величины.
Решение
Запишем исходные данные:
• КПД тепловой машины: η = 0,25.
• Количество теплоты, полученное газом от нагревателя за цикл: Q = 8 Дж.
Формула КПД тепловой машины:
η=AQ
Отсюда:
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | ???? Скачать PDF | Просмотров: 343 | Оценить:
Источник
Второй закон термодинамики указывает направление
возможных энергетических превращений. Английский физик У.
Томсон в 1851 г. сформулировал закон: в природе невозможен
процесс, единственным результатом которого была бы
механическая работа, полученная за счет охлаждения теплового
резервуара. Эта формулировка показывает, что взаимное
превращение тепла и работы неравноценно: работу можно
полностью “превратить” в тепло (путем трения, нагрева
электрическим током и другими способами), а тепло полностью
превратить в работу нельзя.
Чуть раньше У. Томсона формулировку второго закона в 1850 г.
дал немецкий физик Р. Клаузиус (1822-1888): “Теплота не
переходит самопроизвольно от холодного тела к более горячему”.
Эта формулировка подчеркивает односторонность реальных
процессов.
Р. Клаузиус решил вопрос о направлении самопроизвольных
процессов в 1865 г., когда ввел новую функцию –
энтропию, установив ее важнейшую особенность: в
нетеп-лоизолированных системах самопроизвольно процессы идут в
сторону увеличения энтропии; в состоянии теплового равновесия
энтропия достигает максимума. Эта функция является мерой
беспорядка в системе. Таким образом, самопроизвольные процессы
идут в сторону увеличения беспорядка.
Необратимые процессы – процессы, которые могут
самопроизвольно протекать только в одном направлении. Систему,
в которой происходят необратимые процессы, нельзя вернуть в
исходное состояние без того, чтобы в окружающей среде не
осталось каких-либо изменений.
Тепловой двигатель – устройство, в котором
осуществляется преобразование внутренней энергии топлива в
механическую энергию. Тепловой двигатель содержит три основные
части: нагреватель, рабочее тело, холодильник.
Общая блок-схема теплового двигателя представлена на рис. 32.
Чаще всего рабочими телами, совершающими работу в тепловых
двигателях, являются газ или пар.
За один цикл работы рабочее тело получает от нагревателя
количество теплоты Q1. Расширяясь, оно совершает
работу А` и часть количества теплоты Q2 передает
холодильнику: Q1 = А` + Q2.
Охладителем у большинства тепловых двигателей является
окружающая среда (атмосфера).
Тепло, полученное от нагревателя, рабочее тело не может
полностью превратить в механическую энергию путем совершения
работы. Если бы Q1 = А`, то тогда температура
рабочего тела упала до О К, а это, как говорилось выше,
невозможно. Если бы температура рабочего тела оказалась ниже
температуры окружающей среды, то давление газа (пара) было бы
меньше атмосферного и двигатель не смог бы совершать работу.
Коэффициент полезного действия теплового двигателя
равен отношению работы А`, совершенной двигателем за один
цикл, к количеству теплоты Q1, полученной от
нагревателя:
Максимальный КПД имеет тепловой двигатель, работающий по циклу
Карно, состоящему из двух изотерм и двух адиабат.
В 1824 г. С. Карно (1796-1832) доказал теорему: любая реальная
тепловая машина, работающая с нагревателем, имеющим
температуру Т1, и холодильником, имеющим
температуру Т2, не может иметь КПД, превышающий КПД
идеальной тепловой машины, определяемый соотношением :
Из этой формулы следует, что чем больше разность температур
нагревателя и холодильника (т. е. чем дальше в координатах Р-V
отстоят друг от друга изотермы), тем больше
nмах. Но КПД всегда меньше 1
(nнах < 1), так как Т2 > О.
Тепловые Двигатели и Охрана Природы
Влияние тепловых двигателей на окружающую среду заключается в
следующем:
- Выделение в окружающую среду большого количества тепла,
которое должно привести к постепенному повышению
температуры на Земле. - Работа тепловых двигателей сопровождается сжиганием
большого количества угля, нефти и газа. Углекислый газ в
атмосфере наряду с парами воды приводит к “парниковому
эффекту”, что ведет к увеличению температуры Земли. - Топки электростанций, двигатели внутреннего сгорания
выбрасывают в атмосферу вредные для растений, животных и
человека вещества: сернистые соединения, оксиды азота,
углеводороды, окиси углерода и др. - Актуальна проблема захоронения радиоактивных отходов
атомных станций. - Применение паровых турбин на электростанциях требует
больших площадей под пруды для охлаждения отработанного
пара (35% водоснабжения всех отраслей хозяйства).
Источник
Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.
Определение 1
Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.
Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений (ΔU=0):
A=Q
Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3.11.1 в виде диаграммы (p, V) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A1, эквивалентную площади под кривой abc. При сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A=A1+A2 на диаграмме (p, V) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.
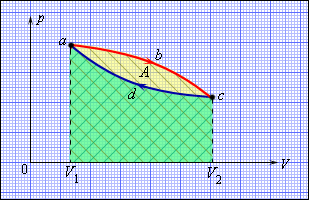
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd.
Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.
Определение 2
Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.
Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q1>0 и теряет, отдавая холодильнику, количество теплоты Q2<0. Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:
Q=Q1+Q2=Q1-Q2.
Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется ΔU=0. Основываясь на первом законе термодинамики, запишем:
∆U=Q-A=0.
Из этого следует:
A=Q=Q1-Q2.
Работа A, которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q.
Определение 3
Коэффициентом полезного действия или же КПД η теплового двигателя называют отношение работы A к полученному рабочим телом за цикл от нагревателя количеству теплоты Q1, то есть:
η=AQ1=Q1-Q2Q1.
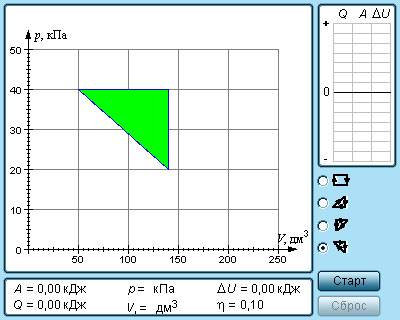
Рисунок 3.11.2. Модель термодинамических циклов.
Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть (1–η) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η<1. На рисунке 3.11.3 проиллюстрирована энергетическая схема тепловой машины.
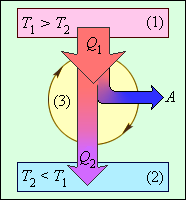
Рисунок 3.11.3. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1>0, A>0, Q2<0; T1>T2.
Виды тепловых двигателей
В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3.11.3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры (1–2, 3–4) и две адиабаты (2–3, 4–1), дизельного двигателя -две адиабаты (1–2, 3–4), одну изобару (2–3) и одну изохору (4–1). Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 %, у дизельного двигателя – приблизительно 40 %.
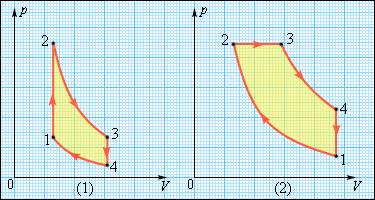
Рисунок 3.11.4. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2).
Цикл Карно
Круговой процесс, изображенный на рисунке 3.11.5, состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.
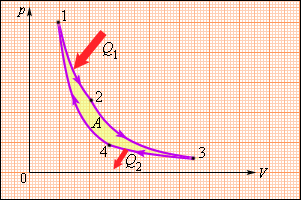
Рисунок 3.11.5. Цикл Карно.
Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы (1–2) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T1. Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A12количество теплоты Q1=A12. После этого на участке адиабаты (2–3) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A23>0. Его температура при адиабатическом расширении снижается до величины T2. На идущем следующим участке изотермы (3–4) газ приводится в тепловой контакт с холодильником в условиях температуры T2<T1. Производится процесс изотермического сжатия. Газом совершается некоторая работа A34<0 и отдается тепло Q2<0, эквивалентное произведенной им работе A34. Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T1, также совершается работа A41<0. совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:
A=A12+A23+A34+A41.
На диаграмме (p, V) данная работа равняется площади цикла.
Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1–2 и 3–4, относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.
Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения ΔU его внутренней энергии. Для 1 моля газа верно следующее выражение:
A=-∆U=-CV(T2-T1),
в котором T1 и T2 представляют собой начальную и конечную температуры рабочего тела.
Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:
A23=-A41.
Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений:
η=AQ1=A12+A34Q12=Q1-Q2Q1=1-Q2Q1.
С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T2и нагревателя T1:
η=T1-T2T1=1-T2T1.
Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:
ηКарно=ηmax

Рисунок 3.11.6. Модель цикла Карно.
Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.
Определение 4
Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.
В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме (p, V) обходятся против часовой стрелки. На рисунке 3.11.7 проиллюстрирована энергетическая схема холодильной машины.
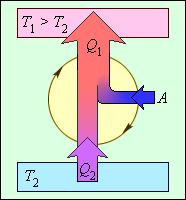
Рисунок 3.11.7. Энергетическая схема холодильной машины. Q1<0, A>0, Q2 > 0, T1>T2.
Работающее по холодильному циклу устройство может обладать двояким предназначением.
Определение 5
Если полезным эффектом является отбор некоторого количества тепла Q2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.
Эффективность работы холодильника может быть охарактеризована следующим отношением:
βx=Q2A.
Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. В условиях подобного определения βх может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:
βx=T2T1-T2.
Определение 6
В случае, когда полезным эффектом является передача некоего количества тепла
|Q1| нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.
Эффективность βТ теплового насоса может быть определена с помощью отношения:
βт=Q1A.
То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
Q1>A.
Следовательно, βТ всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:
βт=1η=T1T1-T2.
Источник