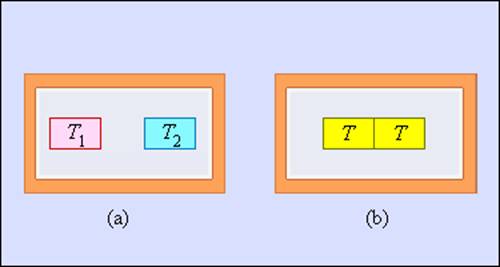
Второе начало термодинамики обратимые тепловые циклы
Определение 1
Первый закон термодинамики – закон сохранения тепловых процессов, устанавливающий связь между количеством теплоты Q и изменением ∆U внутренней энергии и работой А, совершенной над внешними телами:
Q=∆U+A.
Исходя из закона, энергия не может быть создана или уничтожена: производится процесс передачи от одной системы к другой, принимая другую форму. Еще не было получено процессов, нарушающих первый закон термодинамики. Рисунок 3.12.1 показывает устройства, противоречащие первому закону.
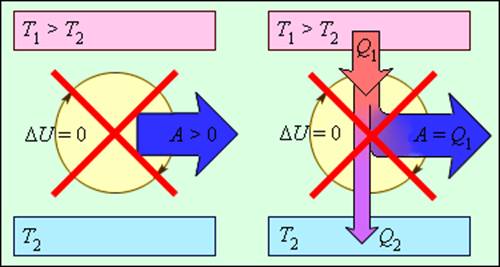
Рисунок 3.12.1. Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η>1.
Обратимый и необратимый процессы
Определение 2
Первый закон термодинамики не устанавливает направления тепловых процессов. Опыты показывают, что большинство тепловых процессов протекают в одном направлении. Их называют необратимыми.
Пример 1
Если имеется тепловой контакт двух тел с разными температурами, тогда направление теплового потока направляется от теплого к холодному. Самопроизвольной передачи тепла от тела с низкой температуры к телу с высокой не наблюдается. Отсюда следует, что теплообмен с конечной разностью температур считается необратимым.
Определение 3
Обратимым процессом называется переход системы из одного равновесного расстояния в другое, которые возможно проводить в обратном направлении в той же последовательности промежуточных равновесных состояний. Она вместе с окружающими телами возвращаются к исходному состоянию.
Если система находится в состоянии равновесия во время процесса, она называется квазистатической.
Когда рабочее тело тепловой машины контактирует с тепловым резервуаром, температура которого неизменна во время всего процесса, то только изотермический квазистатический процесс считается обратимым, так как протекает с бесконечно малой разницей температур рабочего резервуара. Если имеется два резервуара, причем с разными температурами, тогда обратимым путем можно провести процессы на двух изотермических участках.
Так как адиабатический процесс проводится в обоих направлениях (сжатие и расширение), наличие кругового процесса с двумя изотермами и двумя адиабатами (цикл Карно) говорит о том, что это и есть единственный обратимый круговой процесс, где рабочее тело контактируется с двумя тепловыми резервуарами. Остальные при наличии 2 тепловых резервуаров считаются необратимыми.
Превращение механической работы во внутреннюю энергию считаются необратимыми при наличии силы трения, диффузии в газах и жидкостях, а процесс перемешивания по причине начальной разности давлений и так далее. Все реальные процессы считаются необратимыми, даже если значения будут максимально приближены к обратимым. Обратимые рассматриваются как пример реальных процессов.
Первый закон термодинамики не различает их. Правило требует от термодинамического процесса определенного энергетического баланса, но не говорит о том, возможен ли он. Установка направления прохождения процесса определяется вторым законом термодинамики. Его формулировка может звучать как запрет на определенные термодинамические процессы.
Второй закон был трактован У. Кельвином в 1851.
Определение 4
В циклически действующей тепловой машине невозможно прохождение процесса, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.
Предположительно, машина с такими процессами могла бы получить название вечного двигателя второго рода.
Пример 2
При земных условиях могла бы быть отбита энергия Мирового океана и полностью превратилась бы в ее работу. Масса воды Мирового океана – 1021 кг. Для его охлаждения хотя бы на 1 градус потребуется огромное количество энергии ≈1024 Дж, которое сравнимо с сжиганием 1017 кг угля. Вырабатываемая энергия на Земле за год в 104 раз меньше. Отсюда и вывод о том, что вечный двигатель второго рода мало вероятен, как и двигатель первого, потому как оба они недопустимы, исходя из первого закона термодинамики.
Второй закон термодинамики
Формулировка 2-го закона термодинамики была дана физиком Р. Клаузиусом.
Определение 5
Невозможно прохождение процесса, единственным результатом которого была бы передача энергии при помощи теплообмена от тела с низкой температуры к телу с более высокой.
Рисунок 3.12.2 объясняет процессы, которые запрещены вторым законом, но разрешены согласно первому. Они соответствуют трактовкам второго закона термодинамики.
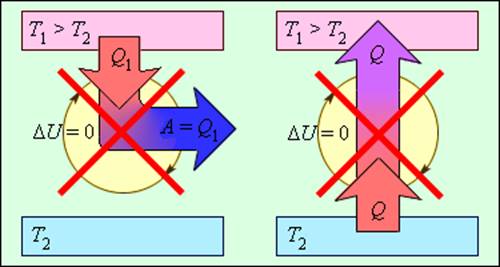
Рисунок 3.12.2. Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – вечный двигатель второго рода; 2 – самопроизвольный переход тепла от холодного тела к более теплому (идеальная холодильная машина).
Формулировки обоих законов считаются эквивалентными.
Пример 3
Когда тело без помощи внешних сил переходит при теплообмене от холодного к горячему, то возникает мысль о возможности создания вечного двигателя второго рода. Если такая машина получит количество теплоты Q1 от нагревателя и отдаст холодильнику Q2, тогда совершается работа A=Q1-Q2. Если бы Q2 самопроизвольно перешло к нагревателю, то конечный результат тепловой машины и идеальной холодильной машины выглядело бы таким образом Q1-Q2. Причем сам переход происходил бы без изменений холодильника. Отсюда вывод – комбинация тепловой машины и идеальной холодильной машины равноценна двигателю второго рода.
Прослеживается связь между вторым законом термодинамики и необратимостью реальных тепловых процессов. Энергия теплового движения молекул отлична от механической, электрической и так далее. Она способна превратиться в другой вид энергии только частично. Поэтому при наличии энергии теплового движения молекул любой процесс считается необратимым, так как полностью в обратном направлении он не осуществим.
Свойство, относящееся к необратимым процессам, говорит о том, что они проходят в термодинамически неравновесной системе, а результат получается в виде замкнутой системы, приближающейся к состоянию термодинамического равновесия.
Теоремы Карно
Имеются теоремы Карно, которые могут быть доказаны, исходя из второго закона термодинамики.
Теорема 1
КПД тепловой машины, работающей при данных значениях температур нагревателя холодильника, не может иметь значение больше, чем КПД действия машины, работающей согласно обратимому циклу Карно с теми же значениями температур нагревателя и холодильника.
Теорема 2
КПД действия тепловой машины, работающей по циклу Карно, не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.
Отсюда следует, что КПД действия машины с циклом Карно считается максимальным.
η=1-Q2Q1≤ηmax=ηКарню=1-T2T1.
Знак равенства данной записи говорит об обратимости процесса. Если машина работает по циклу Карно, тогда:
Q2Q1=T2T1 или Q2T2=Q1T1.
Знаки Q1 и Q2 всегда отличаются независимо от направления цикла. Поэтому получаем:
Q1T1+Q2T2=0.
Рисунок 3.12.3 говорит о том, что данное соотношение обобщается и представляется в виде последовательности малых изометрических и адиабатических участков.
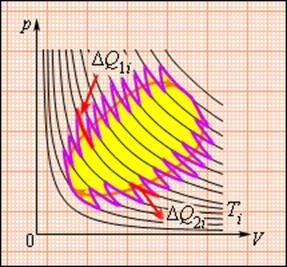
Рисунок 3.12.3. Произвольный обратимый цикл как последовательность малых изотермических и адиабатических участков.
Полный обход замкнутого обратимого цикла имеет вид:
∑∆QiTi=0 (обратимый цикл).
Откуда ∆Qi=∆Q1i+∆Q2i – количество теплоты, полученное рабочим телом на двух изотермических участках с температурой Ti. Чтобы данный цикл провести наоборот, нужно рабочее тело сконтактировать со многими тепловыми резервуарами с Ti.
Энтропия
Определение 6
Отношение QiTi получило название приведенного тепла. Формула показывает, что полное приведенное тепло на любом обратимом цикле равно нулю. Благодаря ей вводится еще одно понятие – энтропия, обозначаемая S. Ее открыл Р. Клаузиус в 1865 году.
При переходе из одного равновесного состояние в другое изменяется и ее энтропия. Разность энтропий двух состояний равняется приведенному теплу, полученному системой во время обратного перехода состояния.
∆S=S2-S1=∑(1)(2)∆QiобрT.
Если рассматривается адиабатический процесс ∆Qi=0, тогда энтропия S не изменяется.
Изменение энтропии ∆S во время перехода в другое состояние фиксируется как формула:
∆S=∫(1)(2)dQобрT.
Определение энтропии достаточно точное. Разность ∆S двух состояний системы подразумевает физический смысл. Если имеется необратимый переход, а необходимо найти энтропию, тогда нужно придумать обратимый процесс, который свяжет начальное и конечное состояние. После этого перейти к нахождению приведенного тепла, полученного системой.
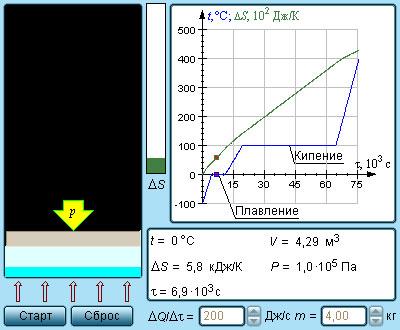
Рисунок 3.12.4Модель энтропии и фазовых переходов.
Рисунок 3.12.5 показывает необратимый процесс расширения шага с отсутствием теплообмена. Равновесными считаются начальное и конечное значение, изображаемые на диаграмме p, V. Точки a и b соответствуют состояниям и располагаются на одной изотерме. Чтобы найти ∆S, следует перейти к рассмотрению обратимого изотермического перехода из a в b. При изопроцессе газ получает определенное количество теплоты окружающих тел Q>0, тогда при необратимом расширении энтропия возрастет до ∆S>0.
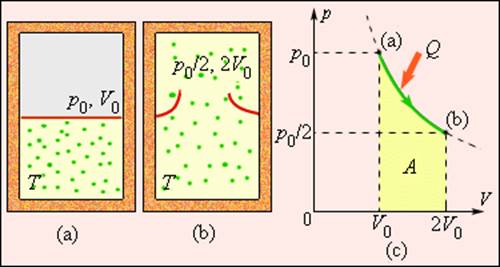
Рисунок 3.12.5. Расширение газа в «пустоту». Изменение энтропии ∆S=QT=AT>0 где A=Q – работа газа при обратимом изотермическом расширении.
Пример 4
Еще одним примером необратимого процесса считается теплообмен при конечной разности температур. Рисунок 3.12.6 и показывает два тела, заключенные в адиабатическую оболочку, где начальные температуры обозначаются как T1 и T2<T1. Течение процесса теплообмена способствует выравниванию температур. Очевидно, что теплое тело отдает, а холодное принимает. Холодное тело превосходит по модулю приведенное тепло, отдаваемое горячим. Отсюда вывод – изменение энтропии в замкнутой системе необратимого процесса ∆S>0.
Рисунок 3.12.6. Теплообмен при конечной разности температур: a – начальное состояние; b – конечное состояние системы. Изменение энтропии ΔS>0.
Все самопроизвольно протекающие процессы в изолированных термодинамических процессах характеризуются ростом энтропии.
Определение 7
Обратимые процессы имеют постоянную энтропию ∆S≥0. Соотношение называют законом возрастания энтропии.
При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо не меняется, либо возрастает.
Определение 8
Наличие энтропии говорит о самопроизвольно протекающем процессе, а ее рост – приближение всей системы к термодинамическому равновесию, где S принимает максимальное значение. Возрастание энтропии можно трактовать как формулировку второго закона термодинамики.
В 1878 году Л. Больцман дал вероятностное определение понятию энтропии, так как было предложено рассматривать ее в качестве меры статистического беспорядка замкнутой термодинамической системы. Все самопроизвольно протекающие процессы в таких системах приближают ее к равновесному состоянию, так как сопровождаются ростом энтропии, и направляют в сторону увеличения вероятности состояния.
Если состояние макроскопической системы содержит большое число частиц, то его реализация может предусматривать несколько способов.
Определение 9
Термодинамическая вероятность W системы – это количество способов, которыми реализуется данное состояние макроскопической системы, макросостояний, осуществляющих его.
Из определения имеем, что W≫1.
Определение 10
При наличии 1 моль газа в емкости существует число N способов размещения молекулы по двум половинам емкости: N=2NА, где NА – число Авогадро. Каждое из них – это микросостояние.
Одно из них соответствует случаю с молекулами, собранными в одной половине сосуда. Вероятность такого события приравнивается к нулю. Большое количество состояний соответствует такому, где молекулы распределяются равномерно по всей площади емкости.
Тогда равновесное состояние является наиболее вероятным.
Определение 11
Равновесное состояние считается состоянием наибольшего беспорядка в термодинамической системе с максимальной энтропией.
Исходя из трактовок Больцмана, энтропия S и термодинамическая вероятность W связаны:
S=k·ln W, где k=1,38·10-23 Дж/К является постоянная Больцмана. Отсюда следует, что определение энтропии определяется логарифмом числа микросостояний. Именно они способствуют реализации данного макросостояния. Тогда энтропия может быть рассмотрена в качестве меры вероятности состояния термодинамической системы.
Определение 12
Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Их называют флуктуациями.
В системах с большим числом частиц отклонения от состояния равновесия имеют достаточно малую вероятность на существование.
Источник
Первый закон термодинамики – закон сохранения энергии для тепловых процессов – устанавливает связь между количеством теплоты Q, полученной системой, изменением ΔU ее внутренней энергии и работой A, совершенной над внешними телами:
Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Процессы, нарушающие первый закон термодинамики, никогда не наблюдались. На рис. 3.12.1 изображены устройства, запрещенные первым законом термодинамики.
|
Рисунок 3.12.1. Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η > 1 |
Первый закон термодинамики не устанавливает направления тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым.
Обратимыми процессами называют процессы перехода системы из одного равновесного состояния в другое, которые можно провести в обратном направлении через ту же последовательность промежуточных равновесных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию.
Процессы, в ходе которых система все время остается в состоянии равновесия, называются квазистатическими. Все квазистатические процессы обратимы. Все обратимые процессы являются квазистатическими.
Если рабочее тело тепловой машины приводится в контакт с тепловым резервуаром, температура которого в процессе теплообмена остается неизменной, то единственным обратимым процессом будет изотермический квазистатический процесс, протекающий при бесконечно малой разнице температур рабочего тела и резервуара. При наличии двух тепловых резервуаров с разными температурами обратимым путем можно провести процессы на двух изотермических участках. Поскольку адиабатический процесс также можно проводить в обоих направлениях (адиабатическое сжатие и адиабатическое расширение), то круговой процесс, состоящий из двух изотерм и двух адиабат (цикл Карно) является единственным обратимым круговым процессом, при котором рабочее тело приводится в тепловой контакт только с двумя тепловыми резервуарами. Все остальные круговые процессы, проводимые с двумя тепловыми резервуарами, необратимы.
Процессы превращения механической работы во внутреннюю энергию тела являются необратимыми из-за наличия трения, процессов диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т. д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов.
Первый закон термодинамики не может отличить обратимые процессы от необратимых. Он просто требует от термодинамического процесса определенного энергетического баланса и ничего не говорит о том, возможен такой процесс или нет. Направление самопроизвольно протекающих процессов устанавливает второй закон термодинамики. Он может быть сформулирован в виде запрета на определенные виды термодинамических процессов.
Английский физик Уильям Кельвин дал в 1851 г. следующую формулировку второго закона:
В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.
Гипотетическую тепловую машину, в которой мог бы происходить такой процесс, называют вечным двигателем второго рода. В земных условиях такая машина могла бы отбирать тепловую энергию, например, у Мирового океана и полностью превращать ее в работу. Масса воды в Мировом океане составляет примерно 1021 кг, и при ее охлаждении на один градус выделилось бы огромное количество энергии (≈ 1024 Дж), эквивалентное полному сжиганию 1017 кг угля. Ежегодно вырабатываемая на Земле энергия приблизительно в 104 раз меньше. Поэтому вечный двигатель второго рода был бы для человечества не менее привлекателен, чем вечный двигатель первого рода, запрещенный первым законом термодинамики.
Немецкий физик Рудольф Клаузиус дал другую формулировку второго закона термодинамики:
Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой.
На рис. 3.12.2 изображены процессы, запрещенные вторым законом, но не запрещенные первым законом термодинамики. Эти процессы соответствуют двум формулировкам второго закона термодинамики.
|
Рисунок 3.12.2. Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – вечный двигатель второго рода; 2 – самопроизвольный переход тепла от холодного тела к более теплому (идеальная холодильная машина) |
Следует отметить, что обе формулировки второго закона термодинамики эквивалентны. Если допустить, например, что тепло может самопроизвольно (т. е. без затраты внешней работы) переходить при теплообмене от холодного тела к горячему, то можно прийти к выводу о возможности создания вечного двигателя второго рода. Действительно, пусть реальная тепловая машина получает от нагревателя количество теплоты Q1 и отдает холодильнику количество теплоты Q2. При этом совершается работа A = Q1 – |Q2|. Если бы количество теплоты |Q2| самопроизвольно переходило от холодильника к нагревателю, то конечным результатом работы реальной тепловой машины и идеальной холодильной машины было бы превращение в работу количества теплоты Q1 – |Q2|, полученного от нагревателя без какого-либо изменения в холодильнике. Таким образом, комбинация реальной тепловой машины и идеальной холодильной машины равноценна вечному двигателю второго рода. Точно также можно показать, что комбинация реальной холодильной машины и вечного двигателя второго рода равноценна идеальной холодильной машине.
Второй закон термодинамики непосредственно связан с необратимостью реальных тепловых процессов. Энергия теплового движения молекул качественно отличается от всех других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично. Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, т. е. он не может быть осуществлен полностью в обратном направлении.
Общим свойством всех необратимых процессов является то, что они протекают в термодинамически неравновесной системе и в результате этих процессов замкнутая система приближается к состоянию термодинамического равновесия.
На основании любой из формулировок второго закона термодинамики могут быть доказаны следующие утверждения, которые называются теоремами Карно:
1. Коэффициент полезного действия тепловой машины, работающей при данных значениях температур нагревателя и холодильника, не может быть больше, чем коэффициент полезного действия машины, работающей по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника.
2. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.
Таким образом, коэффициент полезного действия машины, работающей по циклу Карно, максимален.
Знак равенства в этом соотношении соответствует обратимым циклам. Для машин, работающих по циклу Карно, это соотношение может быть переписано в виде
В каком бы направлении ни обходился цикл Карно (по или против часовой стрелки) величины Q1 и Q2 всегда имеют разные знаки. Поэтому можно записать
Это соотношение может быть обобщено на любой замкнутый обратимый процесс, который можно представить как последовательность малых изотермических и адиабатических участков (рис. 3.12.3).
|
Рисунок 3.12.3. Произвольный обратимый цикл как последовательность малых изотермических и адиабатических участков |
При полном обходе замкнутого обратимого цикла
(обратимый цикл),
где ΔQi = ΔQ1i + ΔQ2i – количество теплоты, полученное рабочим телом на двух изотермических участках при температуре Ti. Для того, чтобы такой сложный цикл провести обратимым путем, необходимо рабочее тело приводить в тепловой контакт со многими тепловыми резервуарами с температурами Ti. Отношение ΔQi / Ti называется приведенным теплом. Полученная формула показывает, что полное приведенное тепло на любом обратимом цикле равно нулю. Эта формула позволяет ввести новую физическую величину, которая называется энтропией и обозначается буквой S (Р. Клаузиус, 1865 г.). Если термодинамическая система переходит из одного равновесного состояния в другое, то ее энтропия изменяется. Разность значений энтропии в двух состояниях равна приведенному теплу, полученному системой при обратимом переходе из одного состояния в другое.
В случае обратимого адиабатического процесса ΔQi = 0 и, следовательно, энтропия S остается неизменной.
Выражение для изменения энтропии ΔS при переходе неизолированной системы из одного равновесного состояния (1) в другое равновесное состояние (2) может быть записано в виде
Энтропия определена с точностью до постоянного слагаемого, так же, как, например, потенциальная энергия тела в силовом поле. Физический смысл имеет разность ΔS энтропии в двух состояниях системы. Чтобы определить изменение энтропии в случае необратимого перехода системы из одного состояния в другое, нужно придумать какой-нибудь обратимый процесс, связывающий начальное и конечное состояния, и найти приведенное тепло, полученное системой при таком переходе.
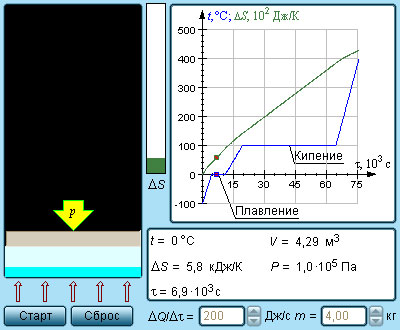 |
Модель. Энтропия и фазовые переходы. |
Рис. 3.12.4 иллюстрирует необратимый процесс расширения газа «в пустоту» в отсутствие теплообмена. Только начальное и конечное состояния газа в этом процессе являются равновесными, и их можно изобразить на диаграмме (p, V). Точки (a) и (b), соответствующие этим состояниям, лежат на одной изотерме. Для вычисления изменения ΔS энтропии можно рассмотреть обратимый изотермический переход из (a) в (b). Поскольку при изотермическом расширении газ получает некоторое количество теплоты от окружающих тел Q > 0, можно сделать вывод, что при необратимом расширении газа энтропия возросла: ΔS > 0.
|
Рисунок 3.12.4. Расширение газа в «пустоту». Изменение энтропии где A = Q – работа газа при обратимом изотермическом расширении |
Другой пример необратимого процесса – теплообмен при конечной разности температур. На рис. 3.12.5 изображены два тела, заключенные в адиабатическую оболочку. Начальные температуры тел T1 и T2 < T1. При теплообмене температуры тел постепенно выравниваются. Более теплое тело отдает некоторое количество теплоты, а более холодное – получает. Приведенное тепло, получаемое холодным телом, превосходит по модулю приведенное тепло, отдаваемое горячим телом. Отсюда следует, что изменение энтропии замкнутой системы в необратимом процессе теплообмена ΔS > 0.
|
Рисунок 3.12.5. Теплообмен при конечной разности температур: a – начальное состояние; b – конечное состояние системы. Изменение энтропии ΔS > 0 |
Рост энтропии является общим свойством всех самопроизвольно протекающих необратимых процессов в изолированных термодинамических системах. При обратимых процессах в изолированных системах энтропия не изменяется:
Это соотношение принято называть законом возрастания энтропии.
При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо остается неизменной, либо увеличивается.
Таким образом, энтропия указывает направление самопроизвольно протекающих процессов. Рост энтропии указывает на приближение системы к состоянию термодинамического равновесия. В состоянии равновесия энтропия принимает максимальное значение. Закон возрастания энтропии можно принять в качестве еще одной формулировки второго закона термодинамики.
В 1878 году Больцман дал вероятностную трактовку понятия энтропии. Он предложил рассматривать энтропию как меру статистического беспорядка в замкнутой термодинамической системе. Все самопроизвольно протекающие процессы в замкнутой системе, приближающие систему к состоянию равновесия и сопровождающиеся ростом энтропии, направлены в сторону увеличения вероятности состояния.
Всякое состояние макроскопической системы, содержащей большое число частиц, может быть реализовано многими способами. Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние. По определению термодинамическая вероятность W >> 1.
Например, если в сосуде находится 1 моль газа, то возможно огромное число N способов размещения молекулы по двум половинкам сосуда: где – число Авогадро. Каждый из них является микросостоянием. Только одно из микросостояний соответствует случаю, когда все молекулы соберутся в одной половинке (например, правой) сосуда. Вероятность такого события практически равна нулю. Наибольшее число микросостояний соответствует равновесному состоянию, при котором молекулы равномерно распределены по всему объему. Поэтому равновесное состояние является наиболее вероятным. С другой стороны равновесное состояние является состоянием наибольшего беспорядка в термодинамической системе и состоянием с максимальной энтропией.
Согласно Больцману, энтропия S системы и термодинамическая вероятность W связаны между собой следующим образом:
где k = 1,38·10–23 Дж/К – постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.
Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Такие отклонения называются флуктуациями. В системах, содержащих большое число частиц, значительные отклонения от состояния равновесия имеют чрезвычайно малую вероятность.
Источник