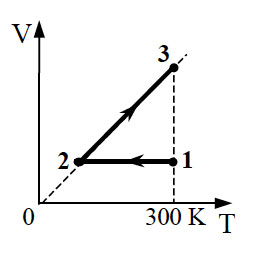
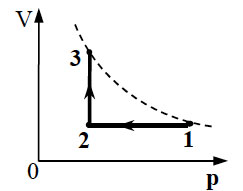
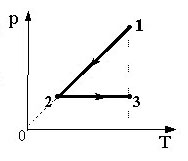
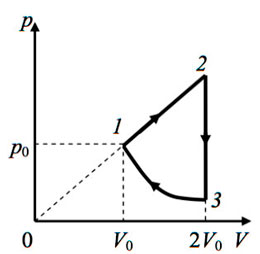
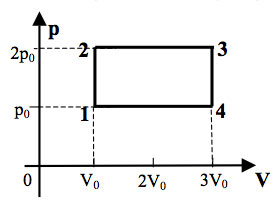
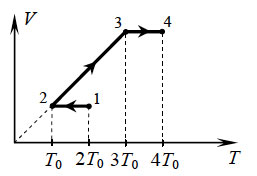
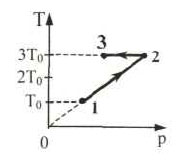
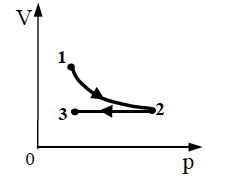
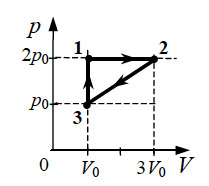
В координатах p t показан цикл тепловой машины у которой
Задачи из ДЕМОВАРИАНТОВ (с решениями)
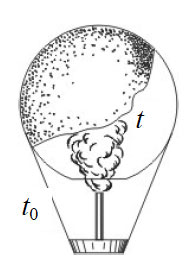
1. Воздушный шар, оболочка
которого имеет массу М = 145 кг и объем V =
230 м3, наполняется горячим воздухом при нормальном
атмосферном давлении и температуре окружающего воздуха tо
= 0оС. Какую минимальную температуру t должен
иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка
шара нерастяжима и имеет в нижней части небольшое отверстие.
Образец возможного решения
2. Воздушный
шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием.
Он может удерживать в воздухе на высоте, где температура воздуха
17оС, а давление 105 Па, груз массой 225
кг. Какова масса гелия в оболочке шара? Считать, что оболочка
шара не оказывает сопротивления изменению объема шара.
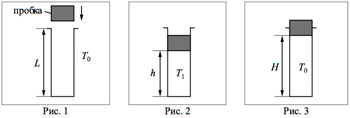
Образец возможного решения2*. В камере, заполненной азотом, при температуре T = 300 К находится открытый цилиндрический сосуд (см. рис. 1). Высота сосуда L = 50 см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры T1. В результате расстояние от дна сосуда до низа пробки становится равным h = 40 см (см. рис. 2). Затем сосуд нагревают до первоначальной температуры T0. Расстояние от дна сосуда до низа пробки при этой температуре становится равным H = 46 см (см. рис. 3). Чему равна температура T1? Величину силы трения между пробкой и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь. Давление азота в камере во время эксперимента поддерживается постоянным.
Образец возможного решения
3. В медный
стакан калориметра массой 200 г, содержащий 150 г воды, опустили
кусок льда, имевший температуру 0°С. Начальная температура калориметра
с водой 25°С. В момент времени, когда наступит тепловое равновесие,
температура воды и калориметра стала равной 5°С. Рассчитайте массу
льда. Удельная теплоемкость меди 390 Дж/кг•К, удельная теплоемкость
воды 4200 Дж/кг•К, удельная теплота плавления льда 3,35•105
Дж/кг. Потери тепла калориметром считать пренебрежимо малыми.
Образец возможного решения4. Необходимо расплавить лёд массой 0,2 кг,
имеющий температуру 0оС. Выполнима ли эта задача,
если потребляемая мощность нагревательного элемента – 400 Вт,
тепловые потери составляют 30%, а время работы нагревателя не
должно превышать 5 минут?
Образец возможного решения4*. Теплоизолированный горизонтальный сосуд разделён пористой перегородкой на две равные части. В начальный момент в левой части сосуда находится ν = 2 моль гелия, а в правой – такое же количество моль аргона. Атомы гелия могут проникать через перегородку, а для атомов аргона перегородка непроницаема. Температура гелия равна температуре аргона: Т = 300 К. Определите отношение внутренних энергий газов по разные стороны перегородки после установления термодинамического равновесия.
Образец возможного решения4**. Теплоизолированный цилиндр разделён подвижным теплопроводным поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К, а аргона – 900 К; объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Поршень медленно перемещается без трения. Теплоёмкость поршня и цилиндра пренебрежимо мала. Чему равно отношение внутренней энергии гелия после установления теплового равновесия к его энергии в начальный момент?
Образец возможного решения
5. В вакууме
закреплен горизонтальный цилиндр с поршнем. В цилиндре находится
0,1 моль гелия. Поршень удерживается упорами и может скользить
влево вдоль стенок цилиндра без трения. В поршень попадает пуля
массой 10 г, летящая горизонтально со скоростью 400 м/с, и застревает
в нем. Температура гелия в момент остановки поршня в крайнем левом
положении возрастает на 64 К. Какова масса поршня? Считать, что
за время движения поршня газ не успевает обменяться теплом с поршнем
и цилиндром.
Образец возможного решения6. В горизонтальном цилиндрическом сосуде,
закрытом поршнем, находится одноатомный идеальный газ. Первоначальное
давление газа p1 = 4•105
Па. Расстояние от дна сосуда до поршня равно L. Площадь
поперечного сечения поршня S = 25 см2. В
результате медленного нагревания газ получил количество теплоты
Q = 1,65 кДж, а поршень сдвинулся на расстояние x
= 10 см. При движении поршня на него со стороны стенок сосуда
действует сила трения величиной Fтр = 3•103
Н. Найдите L. Считать, что сосуд находится в вакууме.
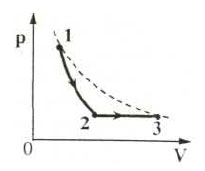
Образец возможного решения7. На pT-диаграмме показан
цикл тепловой машины, у которой рабочим телом является идеальный
газ (см. рисунок). На каком из участков цикла 1 – 2, 2 – 3, 3
– 4, 4 – 1 работа газа наибольшая по модулю?
Образец возможного решения
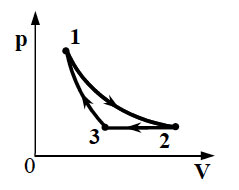
8. 10 моль одноатомного идеального
газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели
до первоначальной температуры 300 К (см. рисунок). Какое количество
теплоты получил газ на участке 2 – 3?
Образец возможного решения
9. 10 моль идеального одноатомного газа охладили,
уменьшив давление в 3 раза. Затем газ нагрели до первоначальной
температуры 300 К (см. рисунок). Какое количество теплоты сообщено
газу на участке 2 – 3?
Образец возможного решения
10. 1 моль идеального одноатомного газа сначала
охладили, а затем нагрели до первоначальной температуры 300
К, увеличив объем газа в 3 раза (см. рисунок). Какое количество
теплоты отдал газ на участке 1 – 2?
Образец возможного решения
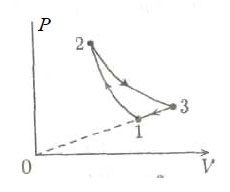
10*. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А12 = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A31| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл холодильнику.
Образец возможного решения
11. Рассчитайте КПД тепловой
машины, использующей в качестве рабочего тела одноатомный идеальный
газ и работающей по циклу, изображенному на рисунке.
Образец возможного решения
Избранные задачи прошлых лет (с ответами)
12. Вертикально расположенный
замкнутый цилиндрический сосуд высотой 50 см разделен подвижным
поршнем весом 110 Н на две части, в каждой из которых содержится
одинаковое количество идеального газа при температуре 361 К. Сколько
молей газа находится в каждой части цилиндра, если поршень находится
на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
13. В калориметре
находился лед при температуре t1 = – 5 °С.
Какой была масса m1 льда, если после добавления
в калориметр m2 = 4 кг воды, имеющей температуру
t2 = 20 °С, и установления теплового равновесия
температура содержимого калориметра оказалась равной t
= 0 °С, причем в калориметре была только вода?14. Теплоизолированный
цилиндр разделен подвижным теплопроводным поршнем на две части.
В одной части цилиндра находится гелий, а в другой — аргон. В
начальный момент температура гелия равна 300 К, а аргона — 900
К. При этом объемы, занимаемые газами одинаковы. Какую температуру
будут иметь газы в цилиндре после установления теплового равновесия,
если поршень перемещается без трения? Теплоемкостью сосуда и поршня
пренебречь.15. Теплоизолированный
сосуд объемом V = 2 м3 разделен теплопроводящей
перегородкой на две части одинакового объема. В одной части находится
m = 1 кг гелия, а в другой части m = 1 кг аргона.
Средняя квадратичная скорость атомов аргона равна средней квадратичной
скорости атомов гелия и составляет υ = 500 м/с. Рассчитайте
парциальное давление гелия после удаления перегородки.16. Теплоизолированный
сосуд объемом V = 2 м3 разделен пористой перегородкой
на две равные части. В начальный момент в одной части сосуда находится
νHe = 2 моль гелия, а в другой – νAr
= 1 моль аргона. Температура гелия ТHe = 300
К, а температура аргона ТAr = 600 К. Атомы
гелия могут свободно проникать через поры в перегородке, а атомы
аргона – нет. Определите температуру гелия после установления
теплового равновесия в системе.17. С одним молем идеального
одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке
в координатах V-Т. Во сколько раз количество теплоты,
полученное газом в процессе 1-2-3-4 больше работы газа в этом
процессе?
18. Один моль одноатомного
идеального газа совершает процесс 1-2-3 (см. рисунок). На участке
2 – 3 к газу подводят 3 кДж теплоты. Т0 =
100 К. Найдите отношение работы, совершаемой газом в ходе всего
процесса А123, к соответствующему полному
количеству подведенной к нему теплоты Q123.
19. Один моль идеального
одноатомного газа сначала изотермически сжали (Т1
= 300 К). Затем газ изохорно охладили, понизив давление в 3 раза
(см. рисунок). Какое количество теплоты отдал газ на участке 2
– 3?
20. Идеальный одноатомный
газ расширяется сначала адиабатно, а затем изобарно. Конечная
температура газа равна начальной (см. рисунок). За весь процесс
1-2-3 газом совершается работа, равная 5 кДж. Какую работу совершает
газ при адиабатном расширении?
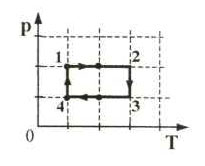
21. На рисунке в координатах
p,T показан цикл тепловой машины, у которой
рабочим телом является идеальный газ. На каком участке цикла работа
газа наименьшая по модулю?
22. Один моль одноатомного
идеального газа совершает цикл, изображенный на pV-диаграмме
(см. рисунок). Участок 1 – 2 –– изотерма, 2 – 3 –– изобара, 3
– 1 –– адиабата. Работа, совершаемая газом за цикл, равна А.
Разность температур в состояниях 1 и 3 составляет ΔТ.
Какую работу совершает газ при изотермическом процессе?
23. Газообразный гелий находится
в цилиндре под подвижным поршнем. Газ сжимают в адиабатическом
процессе, переводя его из состояния 1 в состояние 2 (см. рис.).
Над газом совершается при этом работа сжатия А12
(А12> 0). Затем газ расширяется в изотермическом
процессе 2-3, и, наконец, из состояния 3 газ переводят в состояние
1 в процессе, когда его давление Р прямо пропорционально
объему V. Найти работу А23, которую
совершил газ в процессе изотермического расширения, если во всем
замкнутом цикле 1-2-3-1 он совершил работу А.
24. Температура
гелия увеличилась в k = 3 раза в процессе P2V
= const (Р — давление, V — объем газа), а его
внутренняя энергия изменилась на 100 Дж. Найти: 1) начальный объем
V1 газа; 2) начальное давление P1
газа. Максимальный объем, который занимал газ в процессе нагрева,
равнялся Vmax = 3 л.25. Одноатомный идеальный
газ неизменной массы совершает циклический процесс, показанный
на рисунке. За цикл от нагревателя газ получает количество теплоты
QH = 8 кДж. Чему равна работа газа за цикл?
Ответы к избранным задачам
прошлых лет
Источник
30. Молекулярная физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Два баллона, объёмами 60 л и 40 л, наполнены Неоном 80 г и Гелием 32 г соответственно. После соединения баллонов давление внутри 300 кПа. Определите температуру газов в конце процесса.
“Досрочная волна 2019 вариант 1”
301
Найдем количество газов. Количество неона: [nu_{N}=dfrac{80text{ г}}{20text{ г/моль}}=4text{ моль}] Количество гелия: [nu_H=dfrac{32text{ г}}{4text{ г/моль}}=8text{ моль}] Конечную температуру можно найти из уравнения Клапейрона–Менделеева: [p(V_N+V_N)=(nu_N+nu_H)RT’ Rightarrow T’=dfrac{p(V_N+V_H)}{(nu_N+nu_H)R}=dfrac{300text{ кПа}100text{ л}}{12text{ моль}cdot 8,32text{ дж/(К$cdot$ моль)}}approx 301text{ К}]
Ответ: 301
Постоянную массу идеального одноатомного газа изобарно сжали так, что (T_2=dfrac{T_1}{k}) Затем этот же газ адиабатически расширяется так, что (T_3=dfrac{T_2}{2}) Отношение модулей работ в изобарном и адиабатическом процессах (n=4) Найдите (k).
“Основная волна 2019”
При изобарном сжатии над гахов совершается работа, модуль которой (A_1=|pDelta V|) где (p) – давление гелия в этом процессе, (Delta V) – изменение его объёма.
В соответствии с уравнением Менделеева–Клапейрона для этого процесса можно записать: [pDelta V =nu R (T_1-T_2)=A_1] В адиабатном процессе (процессе без теплообмена) в соответствии с первым законом термодинамики сумма изменения внутренней энергии газа и его работы равна нулю: [dfrac{3}{2}nu R (T_3-T_2)+A_2=0] При записи последнего соотношения учтено выражение для изменения внутренней энергии идеального одноатомного газа: [Delta U =dfrac{3}{2}nu R (T_3-T_2)] Преобразуя записанные уравнения с учётом соотношений температур, заданных в условии задачи, получаем: [A_1=nu RT_2(k-1)hspace{5 mm}A_2=dfrac{3}{4}nu RT_2] По условию (dfrac{A_1}{A_2}=n=4) Следовательно [dfrac{4nu RT_2(k-1)}{3nu R T_2}=4 Rightarrow 4k-4=12 Rightarrow 4k=16 Rightarrow k=4]
Ответ: 4
В вертикальном цилиндре, закрытом лёгким поршнем, находится этиловый спирт ((C_2H_6O)) при температуре кипения (t = 78^circ C). При сообщении спирту количества теплоты (Q) часть его превращается в пар, который при изобарном расширении совершает работу A. Удельная теплота парообразования спирта (L = 846 cdot 10^3) Дж/кг, а его молярная масса – 46(cdot 10^{-3}) кг/моль. Какая часть подведённого к этиловому спирту количества теплоты переходит в работу? Объёмом жидкого этилового спирта пренебречь.
“Основная волна 2020 Вариант 2”
Количество теплоты, полученное системой равно [Q=LDelta m,quad (1)] где (Delta m) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит изменение внутренней энергии будет за счет изменения массы пара [A=dfrac{Delta m}{M}RT,quad (2)] где (T) – температура газа в Кельвинах.
Объединим (1), (2) и (3) и найдем отношение (dfrac{A}{Q}) [dfrac{A}{Q}=dfrac{dfrac{Delta m}{M}RT}{LDelta m}=dfrac{RT}{LM}=dfrac{ cdot 8,31 text{ Дж/(К$cdot$моль)}cdot 351text{ К}}{846cdot 10^3text{ Дж/кг}cdot 46cdot 10^{-3}text{ кг/моль}} approx 0,075]
Ответ: 0,075
Сосуд объемом (V=10) л содержит (nu=5) моль гелий при температуре (t=17^circ C). Если сообщить гелию количество теплоты (Q=3) кДж, то сосуд лопнет. Какую максимальную разность давлений внутри сосуда и снаружи него он выдерживает? Атмосферное давление (p_0=10^5) Па.
“Основная волна 2020 Вариант 3”
Запишем уравнение Клапейрона – Менделеева [p_{max}V=nu R T_{max} quad (1)] где (p_{max}) и (T_{max}) – максимальные давление и температура газа соответственно.
Газ в процессе подвода тепла не увеличивает объем, поэтому работа газа в данном процессе равна 0, следовательно, первый закон термодинамики запишется в виде: [Q=Delta U=dfrac{3}{2}nu r (T_{max}-T_{0})] Выразим отсюда конечную температуру: [T_{max}=dfrac{2Q}{3nu R}+T_0] Подставим конечную температуру в (1) и выразим давление [p_{max}=dfrac{2Q}{3V}+dfrac{nu R T_0}{V}=] Откуда разность давлений [Delta p=p_{max}-p_0=dfrac{2cdot 30000text{ Дж}}{3cdot 10^{-2}text{ м$^3$}}+dfrac{5text{ моль}cdot 8,31text{ Дж/(моль$cdot$ К)}cdot 290text{ К}}{10^{-2}text{ м$^3$}}-10^5text{ Па}=1’304’950text{ Па}]
Ответ: 1304950
Гелий в количестве (nu) = 3 моль изобарно сжимают, совершая работу (A_1) = 2,4 кДж. При этом температура гелия уменьшается в 4 раза: (T_2=dfrac{T_1}{4}) . Затем газ адиабатически расширяется, при этом его температура изменяется до значения (T_3=dfrac{T_1}{8}). Найдите работу газа (A_2) при адиабатном расширении. Количество вещества в процессах остаётся неизменным.
“Демоверсия 2020”
При изобарном сжатии над гелием совершается работа, модуль которой (A_1=|pDelta V|) где (p) – давление гелия в этом процессе, (Delta V) – изменение его объёма.
В соответствии с уравнением Менделеева–Клапейрона для этого процесса можно записать: [pDelta V =nu R (T_1-T_2)] В адиабатном процессе (процессе без теплообмена) в соответствии с первым законом термодинамики сумма изменения внутренней энергии газа и его работы равна нулю: [dfrac{3}{2}nu R (T_3-T_2)+A_2=0] При записи последнего соотношения учтено выражение для изменения внутренней энергии идеального одноатомного газа: [Delta U =dfrac{3}{2}nu R (T_3-T_2)] Преобразуя записанные уравнения с учётом соотношений температур, заданных в условии задачи, получаем: [A_1=3nu RT_2hspace{5 mm}A_2=dfrac{3}{4}nu RT_2] Получаем: [A_2=dfrac{A_1}{4}=600text{ Дж}]
Ответ: 600
В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол ((C_6H_6)) при температуре кипения (t=80^circ C) . При сообщении бензолу количества теплоты (Q) часть его превращается в пар, который, при изобарном расширении, совершает работу (A). Удельная теплота парообразования бензола (396cdot 10^3text{ Дж/кг}), его молярная масса (78cdot 10^{-3}text{ кг/моль}) кг/моль. Какая часть подведённого к бензолу количества теплоты переходит в работу? Объёмом жидкого бензола пренебречь.
“Демоверсия 2021”
Количество теплоты, полученное системой равно [Q=LDelta m,quad (1)] где (Delta m) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит изменение внутренней энергии будет за счет изменения массы пара [A=dfrac{Delta m}{M}RT,quad (2)] где (T) – температура газа в Кельвинах.
Объединим (1), (2) и (3) и найдем отношение (dfrac{A}{Q}) [dfrac{A}{Q}=dfrac{dfrac{Delta m}{M}RT}{LDelta m}=dfrac{RT}{LM}=dfrac{ 8,31 text{ Дж/(К$cdot$моль)}cdot 353text{ К}}{ 396cdot 10^3text{ Дж/кг}cdot 78cdot 10^{-3}text{ кг/моль}} = 9,5%]
Ответ: 9,5
С одним молем идеального одноатомного газа проводят циклический процесс 1-2-3-1, где 1-2 – адиабата, 2-3 – изобара, 3-1 – изохора. Температуры в точках 1, 2, 3 равны 600 К, 455 К и 300 К соответственно. Найдите КПД цикла.

“Досрочная волна 2019 вариант 2”
Цикл не является циклом идеальной тепловой машины. Поэтому воспользуемся общей формулой через теплоту нагревателя и теплоту холодильника. [eta = dfrac{Q_text{н}-_text{х}}{_text{н}}=1-dfrac{Q_text{х}}{Q_text{н}}] Необходимо выяснить, на каком из участков цикла газ получает тепло от нагревателя, а на каком – отдаёт холодильнику. Для этого проведём подсчёт теплоты каждого участка по 1-му началу термодинамики [Q=A+Delta U] 1. На участке 1–2 представлена адиабата — по определению количество теплоты на этом участке равно нулю: (Q_{12}=0) 2. На участке 2–3 представлен изобарный процесс. Тут нужно подсчитать и работу газа и внутреннюю энергию
[Q_{23}=A_{23}+Delta U_{23}=p_{2}left(V_{3}-V_{2}right)+frac{3}{2} v Rleft(T_{3}-T_{2}right)=] [=left(p_{2} V_{3}-p_{2} V_{2}right)+frac{3}{2} v Rleft(T_{3}-T_{2}right)=left(v R T_{3}-v R T_{2}right)+frac{3}{2} v Rleft(T_{3}-T_{2}right)=] [=frac{5}{2} v Rleft(T_{3}-T_{2}right)<0] [Q_text{х}=left|Q_{23}right|=frac{5}{2} v Rleft(T_{2}-T_{3}right)] 3.На участке 3–1 объём газ постоянен, работа равна нулю: [Q_{31}=A_{31}+Delta U_{31}=Delta U_{31}=frac{3}{2} v Rleft(T_{1}-T_{3}right)>0] Теплота получилась на этом участке положительной, а значит, газ получает теплоту от нагревателя [Q_text{н}=Q_{31}=frac{3}{2} v Rleft(T_{1}-T_{3}right)] 4. Найдём значение КПД: [eta=1-frac{Q_text{х}}{Q_text{н}}=1-frac{sum_{2} v Rleft(T_{2}-T_{3}right)}{3 v Rleft(T_{1}-T_{3}right)}=1-frac{5}{3} cdot frac{T_{2}-T_{3}}{T_{1}-T_{3}}] [eta=1-frac{5}{3} cdot frac{455-300}{600-300}=1-frac{31}{36}=frac{5}{36} approx 0,139=13,9 %]
Ответ:
Источник