В идеальном тепловом двигателе работающем по циклу карно абсолютная
Идеальный цикл Карно
Мы, как простые обыватели, редко задумываемся над тем, как работают тепловые двигателя, и уж тем более – не пытаемся вникнуть в суть происходящего внутри этих самых двигателей с точки зрения термодинамики. Среднестатистические познания механиков и техников ограничиваются тем, что, вроде как, что-то там внутри сгорает, и благодаря этому начинают шевелиться поршни (в простонародье – “поршня”), вращая другие детали и, как говорится, “процесс пошел”.
Но, как всегда, среди людского роду-племени находятся наиболее дотошные представители, которым просто необходимо знать, как на самом деле все происходит и от чего все зависит. Наверное, на этих “дотошных” и “вездесущих”, как на ветках деревьев и произрастают плоды, вскармливающие науку.
Итак, давайте попробуем разобраться – как же работает тепловой двигатель, и от чего зависит его эффективность?
Немного теории.
Тепловым двигателем называют такую машину, которая способна преобразовывать энергию тепла в энергию механического движения. Т. е. внутри этих механизмов, представляющих собой систему, что-то начинает вращаться, перемещаться и кувыркаться, если каким-либо образом изменить температуру внутри этой самой системы (как правило, тепло подводят к рабочему телу, которое чаще всего по ряду “уважительных” причин является газом).
Ну и еще немного – все двигатели подразделяют, по большому счету, на двигатели внутреннего сгорания и двигатели внешнего сгорания.
У первых подвод тепла к элементу системы совершается внутри двигателя, у вторых – где-то снаружи. Забегая вперед, приведем пример: к двигателям внешнего сгорания относят, в частности, паровые двигатели, в которых тепло к рабочему телу (льду, воде или пару или какой-либо жидкости) подводится вне двигателя, путем сжигания какого-нибудь топлива (угля, мазута, дров и т. п.) в отдельно расположенной топке под емкостью (котлом) с рабочим телом. Потом разогретое рабочее тело вводится в тепловой двигатель (поступает в цилиндр), и совершает полезную работу, отдавая при этом теплоту.
К двигателям внутреннего сгорания (ДВС) относятся (например) всем с детства знакомые дизели и карбюраторные двигатели, у которых рабочее тело сжигается и выделяет тепло внутри системы (в цилиндре).
И в том и в другом случае речь идет о термодинамических процессах, т.е. процессах, вызывающих температурные колебания (или вызываемых температурными колебаниями) внутри системы.
В общем случае суть происходящего с точки зрения современной термодинамики описана здесь.
В начале XIX века талантливым французским инженером Сади Карно (1796-1832) были изучены термодинамические процессы, имеющие место в тепловых машинах, использующих в качестве рабочего тела идеальный газ. При этом все процессы в машинах рассматривались им как равновесные (обратимые).
Обратимый процесс – это такой процесс, который протекает настолько медленно, что его можно рассматривать как последовательный переход от одного равновесного состояния к другому и т. д., причём весь этот процесс можно провести в обратном направлении без изменения совершённой работы и переданного количества теплоты. (Следует отметить, что все реальные процессы необратимы).
Целью исследований Карно было определение условий, при которых можно получить максимальную работу из теплоты, подведенной к тепловой машине, т. е. наиболее эффективно преобразовать тепловую энергию в механическую.
В конце XVIII – начале XIX века единственным типом тепловых машин, используемых человечеством в практических целях, являлись двигатели внешнего сгорания – т. е. паровые машины. КПД этих машин был чрезвычайно низким – не более 2 %, при этом не существовало какой-либо убедительной теории, указывающей пути к повышению их эффективности.
Карно провел тщательный анализ различных способов преобразования теплоты в работу на примере идеализированной модели поршневой паровой машины, при этом результаты и выводы, сделанные им, оказались справедливыми для любого типа машин, использующими тепловую энергию для выполнения механической работы.
В результате теоретических умозаключений Карно пришел к выводу, что максимального эффекта от преобразования теплоты в механическую энергию можно достичь, используя круговой цикл, состоящий из четырех последовательных процессов – изотермического, адиабатного, изотермического и опять адиабатного, который завершал цикл, возвращая систему к исходному состоянию.
Эта последовательность термодинамических процессов в тепловой машине получила название идеальный цикл Карно.
Изготовить реальный двигатель, преобразующий энергию тепла в механическую энергию строго по циклу, предложенному Карно, невозможно по технологическим причинам, поэтому цикл Карно считается неосуществимым и идеальным.
Николя Леонар Сади Карно считается одним из основателей термодинамики. В 28 лет он написал единственный дошедший до потомков труд – «Размышления о движущей силе огня и о машинах, способных развивать эту силу», в которой изложил принципиально новые для того времени взгляды на процессы в тепловых машинах, нашедшие отражение во втором законе термодинамики.
Сади Карно ввел в научную терминологию основные понятия термодинамики – идеальная тепловая машина, идеальный цикл, обратимость и необратимость термодинамических процессов.
В начале XIX века использовались лишь примитивные паровые машины, КПД которых не превышал несколько процентов, поскольку не существовало теории, способной разъяснить способы повышения эффективности использования тепловой энергии в двигателях. Работа Карно послужила первым путеводителем для инженеров в поисках эффективного использования теплоты в двигателях.
Карно умер совсем молодым, в возрасте 36 лет от заболевания холерой.
Поскольку в те годы холера считалась ужасным и неизлечимым недугом, тела и вещи умерших полагалось сжигать. Наверняка в огне погибли многие ценные труды этого талантливейшего инженера. Чудом уцелели лишь ставшие знаменитыми «Размышления о движущих силах огня…», которые этот самый огонь, уничтоживший все прочие труды Карно и его безжизненное тело, пожалел…
***
Последовательность процессов в цикле Карно
Рассмотрим предложенную Карно последовательность термодинамических процессов, получившую название идеальный цикл Карно.
Как известно, механическая работа может совершаться термодинамической системой лишь в том случае, когда протекает процесс, сопровождающийся изменением объема рабочего тела, т. е. изотермический, изобарный или адиабатный. При этом вся тепловая энергия может быть преобразована в работу лишь при изотермическом процессе (при изобарном и адиабатном процессе часть теплоты расходуется на изменение внутренней энергии рабочего тела).
При изохорном процессе (протекающем при неизменном объеме рабочего тела) превращения теплоты в механическую работу исключается.
В исходном состоянии идеального цикла Карно рабочее тело (идеальный газ) имеет некоторые параметры p1, V1, T1.
К рабочему телу от внешнего источника, называемого нагревателем, подводится теплота, которую система (тепловая машина) начинает использовать по изотермическому процессу.
Как отмечалось выше, при изотермическом процессе переменными являются два основных параметра рабочего тела – давление и объем, соотношение между которым обратно пропорционально (закономерность Бойля-Мариотта). При этом вся подведенная к рабочему телу теплота расходуется исключительно на совершение механической работы; внутренняя энергия рабочего тела остается неизменной и затрат теплоты, полученной от внешнего нагревателя, не требует. Поэтому выбор первого термодинамического процесса в цикле Карно по изотерме вполне логичен – это позволяет максимально использовать полученное от нагревателя тепло для выполнения механической работы.
По окончании изотермического процесса рабочее тело имеет параметры p2, V2, T1.
Этот процесс цикла Карно на диаграмме (рис. 1) обозначен цифрами 1-2.
Поскольку цикл Карно является обратимым и круговым, т. е. все протекающие в нем термодинамические процессы должны возвращать рабочее тело к исходным параметрам, становится очевидным, что в цикле должен присутствовать еще хотя бы один изотермический процесс. При этом его течение должно сопровождаться охлаждением рабочего тела, т. е. передачей теплоты от системы во внешнюю среду, иначе к точке с начальными параметрами не вернуться. Если сразу после первого процесса запустить второй изотермический процесс, то суммарная работа цикла будет минимальна, поскольку площадь графика, характеризующая выполненную системой механическую работу (на рис. 1 заштрихована) будет мала или вообще равна нулю (если прямая и обратная изотермы совпадают).
По этой причине С. Карно в качестве второго термодинамического процесса для своего цикла применил адиабатный процесс, протекающий без теплообмена системы с внешней средой. При этом работа выполняется за счет изменения внутренней энергии рабочего тела, которое продолжает расширяться и охлаждаться до температуры Т2. На диаграмме цикла Карно этот участок заключен между цифрами 2-3.
Использование адиабатного процесса вслед за изотермическим позволяет получить от системы некоторую механическую работу уже без подвода теплоты от нагревателя, за счет использования внутренней энергии рабочего тела.
Параметры рабочего тела по окончанию этого процесса – p3, V3, T2.
Следующим звеном цикла Карно является второй изотермический процесс, который, как уже рассматривалось выше, должен быть отрицательным, т. е. сопровождаться передачей тепла от рабочего тела во внешнюю среду другому телу, называемому в данном случае холодильником.
На диаграмме цикла этот процесс обозначен цифрами 3-4.
Течение процесса сопровождается уменьшением объема и увеличением давления рабочего тела (сжатием), при этом его температура остается постоянной за счет отдачи тепла холодильнику.
Параметры рабочего тела по окончании этого процесса – p4, V4, T2.
Заключительный процесс цикла Карно, возвращающий систему в исходное состояние с начальными параметрами p1, V1, T1 – адиабатный.
Передача тепла холодильнику прекращается. При этом рабочее тело продолжает уменьшаться в объеме (сжиматься), за счет совершения над ним некоторой внешней работы, которая для процесса является отрицательной.
Внутренняя энергия рабочего тела при этом увеличивается, поскольку часть внешней работы расходуется на его нагрев.
Этот процесс на диаграмме обозначен цифрами 4-1.
Для современного специалиста-теплотехника предложенный Карно цикл вполне логичен и не вызовет особых эмоций – наиболее рациональное превращение теплоты в механическую энергию не может осуществляться по иному пути, как с помощью изотермического процесса. Возврат к начальной точке цикла без затрат энергии на паразитные внутренние процессы системы тоже должен проходить по изотерме. А в качестве промежуточных процессов, исключающих потери теплоты во внешнюю среду, наиболее логичны процессы адиабатные.
Тем не менее, не следует забывать, что на момент написания «Размышлений о движущей силы огня и о машинах, способных развивать эту силу» никаких теоретических изысканий в области тепловых двигателей не проводилось, поэтому труд молодого француза был поистине революционным.
Анализ полученной Карно круговой p-V диаграммы цикла показывает, что системой выполнена механическая работа, величина которой характеризуется площадью, заключенной между кривой, ограниченной точками 1-2-3 и кривой, ограниченной точками 3-4-1. При этом вся выполненная системой работа будет равна сумме работ, выполненных в течение каждого из четырех последовательных термодинамических процессов, перечисленных выше.
Очевидно, что работа, выполненная рабочим телом в течение прямого и обратного адиабатных процессов равна по величине, но имеет разный знак (положительная в первом процессе, и отрицательная во втором), т. е. сумма этих работ равна нулю. А работа, выполненная в течение прямого изотермического процесса больше, чем работа, совершенная во время обратного изотермического процесса.
Графически это поясняется разной площадью диаграммы, заключенной между абсциссой и соответственно первой и второй изотермой. Чем выше расположена первая изотерма на диаграмме относительной второй (обратной) изотермы, тем большую работу совершит рабочее тело.
Если рассмотреть T-V диаграмму процесса, то она будет представлять плоскую фигуру (например, ромб), в которой две изотермы (прямая и обратная) параллельны одной из осей (температурной), а адиабаты будут параллельны друг другу.
Из этого следует, что выполненная системой полезная работа будет тем больше, чем больше разница между температурой нагревателя и температурой холодильника, т. е. чем больше перепад температур между Т1 и Т2 (расстояние между верхней и нижней изотермой на T-V диаграмме).
Математический анализ предложенной Сади Карно модели идеального цикла показывает, что максимальный термический КПД тепловой машины может быть определен из соотношения:
ηt = 1 – T2/T1;
где: Т1 и Т2 – температура рабочего тела (газа) соответственно в начале и конце цикла.
Эта простая формула позволяет сделать два основных вывода – о пути повышения КПД тепловых машин и о том, что невозможно создать тепловую машину, коэффициент полезного действия которой будет равен единице, т. е. 100 %. Действительно – дробь Т2/Т1 может быть равна нулю лишь в том случае, если ее числитель равен нулю, либо знаменатель равен бесконечности. И то и другое – нереально, поскольку невозможно охладить материальное тело до температуры абсолютного нуля, и невозможно начальную температуру рабочего тела сделать бесконечной, поскольку само понятие тела в этом случае потеряет смысл; кроме того – невозможно изготовить реальный двигатель, детали и узлы которого способны выдержать такую температуру.
Цикл Карно является эталоном, к которому стремятся инженеры, проектирующие тепловые машины. В условиях реальных температур, верхний предел которых определяется прочностью материалов, а нижний соответствует температуре окружающей среды, термический КПД цикла Карно может достигать величины 0,7…0,8.
Любой реальный тепловой двигатель будет тем совершеннее, чем ближе его КПД к расчетному КПД цикла Карно, протекающего в тех же температурных границах.
***
История создания тепловых двигателей
Скачать теоретические вопросы к экзаменационным билетам
по учебной дисциплине “Основы гидравлики и теплотехники”
(в формате Word, размер файла 68 кБ)
Скачать рабочую программу
по учебной дисциплине “Основы гидравлики и теплотехники” (в формате Word):
- для специальности СПО “Механизация сельского хозяйства”
- для специальности СПО “Техническое обслуживание и ремонт автомобильного транспорта”
Скачать календарно-тематический план
по учебной дисциплине “Основы гидравлики и теплотехники” (в формате Word):
- для специальности СПО “Механизация сельского хозяйства”
- для специальности СПО “Техническое обслуживание и ремонт автомобильного транспорта”
Источник
Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.
Определение 1
Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.
Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений (ΔU=0):
A=Q
Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3.11.1 в виде диаграммы (p, V) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A1, эквивалентную площади под кривой abc. При сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A=A1+A2 на диаграмме (p, V) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.
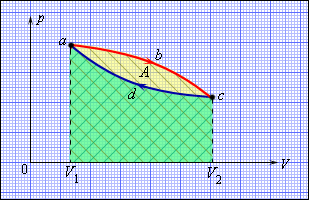
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd.
Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.
Определение 2
Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.
Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q1>0 и теряет, отдавая холодильнику, количество теплоты Q2<0. Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:
Q=Q1+Q2=Q1-Q2.
Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется ΔU=0. Основываясь на первом законе термодинамики, запишем:
∆U=Q-A=0.
Из этого следует:
A=Q=Q1-Q2.
Работа A, которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q.
Определение 3
Коэффициентом полезного действия или же КПД η теплового двигателя называют отношение работы A к полученному рабочим телом за цикл от нагревателя количеству теплоты Q1, то есть:
η=AQ1=Q1-Q2Q1.
Рисунок 3.11.2. Модель термодинамических циклов.
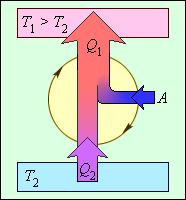
Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть (1–η) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η<1. На рисунке 3.11.3 проиллюстрирована энергетическая схема тепловой машины.
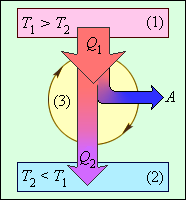
Рисунок 3.11.3. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1>0, A>0, Q2<0; T1>T2.
Виды тепловых двигателей
В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3.11.3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры (1–2, 3–4) и две адиабаты (2–3, 4–1), дизельного двигателя -две адиабаты (1–2, 3–4), одну изобару (2–3) и одну изохору (4–1). Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 %, у дизельного двигателя – приблизительно 40 %.
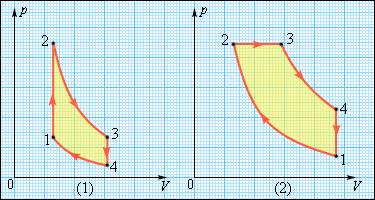
Рисунок 3.11.4. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2).
Цикл Карно
Круговой процесс, изображенный на рисунке 3.11.5, состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.
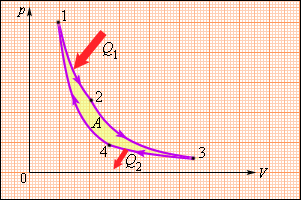
Рисунок 3.11.5. Цикл Карно.
Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы (1–2) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T1. Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A12количество теплоты Q1=A12. После этого на участке адиабаты (2–3) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A23>0. Его температура при адиабатическом расширении снижается до величины T2. На идущем следующим участке изотермы (3–4) газ приводится в тепловой контакт с холодильником в условиях температуры T2<T1. Производится процесс изотермического сжатия. Газом совершается некоторая работа A34<0 и отдается тепло Q2<0, эквивалентное произведенной им работе A34. Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T1, также совершается работа A41<0. совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:
A=A12+A23+A34+A41.
На диаграмме (p, V) данная работа равняется площади цикла.
Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1–2 и 3–4, относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.
Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения ΔU его внутренней энергии. Для 1 моля газа верно следующее выражение:
A=-∆U=-CV(T2-T1),
в котором T1 и T2 представляют собой начальную и конечную температуры рабочего тела.
Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:
A23=-A41.
Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений:
η=AQ1=A12+A34Q12=Q1-Q2Q1=1-Q2Q1.
С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T2и нагревателя T1:
η=T1-T2T1=1-T2T1.
Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:
ηКарно=ηmax
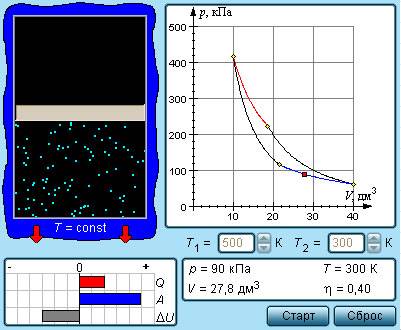
Рисунок 3.11.6. Модель цикла Карно.
Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.
Определение 4
Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.
В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме (p, V) обходятся против часовой стрелки. На рисунке 3.11.7 проиллюстрирована энергетическая схема холодильной машины.

Рисунок 3.11.7. Энергетическая схема холодильной машины. Q1<0, A>0, Q2 > 0, T1>T2.
Работающее по холодильному циклу устройство может обладать двояким предназначением.
Определение 5
Если полезным эффектом является отбор некоторого количества тепла Q2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.
Эффективность работы холодильника может быть охарактеризована следующим отношением:
βx=Q2A.
Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. В условиях подобного определения βх может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:
βx=T2T1-T2.
Определение 6
В случае, когда полезным эффектом является передача некоего количества тепла
|Q1| нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.
Эффективность βТ теплового насоса может быть определена с помощью отношения:
βт=Q1A.
То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
Q1>A.
Следовательно, βТ всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:
βт=1η=T1T1-T2.
Источник