Умножение за один цикл

Хочу рассказать читателям о программистском трюке, с которым я познакомился в какой-то переводной книжке, содержащей подборку таких трюков, в те далёкие времена, когда ещё не изобрели не то что байт, а страшно сказать – стек, а великий Дейкстра ещё не проклял оператор GOTO (sic, in uppercase).

Трюк настолько мне понравился простотой и изяществом, что уже в этом тысячелетии я с удовольствием рассказывал о нём студентам в виде следующей задачи.

Представьте себе, что в процессе возвращения в 2030 году с Луны вы вдруг обнаружили, что ваш бортовой компьютер неправильно выполняет операции целочисленного умножения, и это непременно приведёт к аварии при посадке.

В таком сюжете нет ничего особо фантастического. Вспомним, например, какие проблемы случались когда-то с процессорами Pentium , а к моменту отправки на Луну вы ещё не достигли полного импортозамещения. И вообще надо проверить, а не были ли процессоры просверлены специально.

Но к делу. Вам надо срочно реализовать умножение программно, чтоб работало быстро в реальном времени и укладывалось в доступный ресурс.

Из школьного курса арифметики вспоминаем, что многозначные числа умножать можно столбиком, а результат умножения отдельных цифр брать из таблицы умножения.

Вот только если цифры выбрать короткими (например 0 и 1), таблица умножения будет короткой, а столбики длинными, и их вычисление будет занимать много времени.

Если, наоборот, взять цифры длинные (например от 0 до 65535), то для 16-битной арифметики

результат берётся прямо из таблицы, а столбики отсутствуют. Однако размер классической таблицы Пифагора при этом оказывается около 17GB (4*65536*65536), если учесть симметрию относительно диагонали, то половина – около 8.5GB.

Может оказаться многовато.

Напрягаемся и вспоминаем алгебру.

(1)

(2)

Вычитаем (2) из (1)

и далее

Таким образом, имея таблицу квадратов в массиве sqr, получаем

a * b = ( sqr[a + b] – sqr[a – b]) / 4 (*)

Размер таблицы 8*(65535+65535) около 8.4MB, что уже может оказаться приемлемым.

Размер элемента таблицы в 8 байт связан с тем, что при максимальных a и b квадрат их суммы в 4 байта не влезает – не хватает 2-х бит.

Далее опишу некоторое улучшение, которого в книжке не было. Его я придумал сам, когда уже писал эту заметку.

Заметим, что два младших бита квадрата чётного числа всегда 00, а квадрата нечётного – всегда 01. С другой стороны для любой пары чисел их сумма и разность имеют одинаковую чётность.

Поэтому в нашей формуле (*) процесс вычитания в скобках не может иметь переносов,

связанных с двумя младшими битами. Поэтому содержимое элементов таблицы квадратов

можно заранее сдвинуть на два бита вправо и тем самым сэкономить половину памяти.

Окончательно имеем

a * b = sqr4[a + b] – sqr4[a – b] (**)

где sqr4 – модифицированная таблица квадратов.

В нашем примере её размер около 4.2 MB.

Ниже для иллюстрации этого подхода включен текст программы на языке Lua.

create_multiplier(N) — N это число разных цифр local sqr4 = {} — создаём таблицу for i = 1, 2 * N – 1 do local temp = 0 for j = 1, i – 1 do — для вычисления квадрата temp = temp + i – 1 — используем многократное сложение end — т.к. умножение “неисправно” sqr4[i] = math.(temp / 4) — экономим 2 бита end return — возвращаем мультипликатор (функцию) (i, j) if i < j then i, j = j, i end return sqr4[1 + i + j] – sqr4[1 + i – j] end end N = 256 mpy = create_multiplier(N) for i = 0, N – 1 do for j = 0, N – 1 do if i * j ~= mpy(i,j) then (“Ошибка”, i, j, i * j, mpy(i,j)) end end end (“Всё работает.”)

Для современных процессоров представляется разумным иметь размер цифр кратным размеру байта для лёгкого доступа к ним. При цифрах размером в 1 байт, размер таблицы всего лишь 1022 байт, что может позволить использовать этот трюк в 8-битных процессорах, не имеющих аппаратного умножения.

Буду благодарен всем читателям этой заметки за исправления и замечания.

Источник

В вычислениях , особенно в обработке цифровых сигналов , операция умножения-накопления является обычным шагом, на котором вычисляется произведение двух чисел и складывается это произведение в сумматор . Аппаратный блок, выполняющий операцию, известен как умножитель-накопитель ( MAC или MAC-блок ); сама операция также часто называется операцией MAC или MAC. Операция MAC изменяет аккумулятор a :

Когда это делается с числами с плавающей запятой , это может быть выполнено с двумя округлениями (типично для многих DSP ) или с одним округлением. Когда выполняется с одним округлением, это называется объединенным умножением-сложением ( FMA ) или объединенным умножением-накоплением ( FMAC ).

Современные компьютеры могут содержать выделенный MAC, состоящий из умножителя, реализованного в комбинационной логике, за которым следует сумматор и регистр накопителя, в котором хранится результат. Выходной сигнал регистра возвращается на один вход сумматора, так что в каждом тактовом цикле выход умножителя добавляется к регистру. Комбинационные множители требуют большого количества логики, но могут вычислить произведение намного быстрее, чем метод сдвига и сложения, типичный для более ранних компьютеров. Перси Ладгейт был первым, кто задумал MAC в своей Аналитической машине 1909 года, и первым, кто использовал MAC для деления (используя умножение с засеваемым на обратное, через сходящийся ряд (1+ x ) -1 ). Первыми современными процессорами, оснащенными блоками MAC, были цифровые сигнальные процессоры , но теперь этот метод также широко используется в процессорах общего назначения.

В арифметике с плавающей запятой

Когда выполняется с целыми числами , операция обычно точная (вычисляется по модулю некоторой степени двойки ). Однако числа с плавающей запятой обладают лишь определенной математической точностью . То есть цифровая арифметика с плавающей запятой обычно не является ассоциативной или распределительной . (См. Плавающая точка § Проблемы точности .) Следовательно, для результата имеет значение, выполняется ли умножение-сложение с двумя округлениями или с одной операцией с одним округлением (объединенное умножение-сложение). IEEE 754-2008 указывает, что это должно выполняться с одним округлением, что дает более точный результат.

Слитное умножение – сложение

Слиты умножения-сложения ( ФМА или fmadd ) является плавающей точкой умножения-сложения операция , выполняемая на одном этапе, с одним округлением. То есть, если несвязанное умножение – сложение вычислит произведение b × c , округлит его до N значащих битов, добавит результат к a и вернет обратно к N значащим битам, объединенное умножение – сложение вычислит все выражение a + ( b × c ) до полной точности перед округлением конечного результата до N значащих битов.

Быстрая FMA может ускорить и повысить точность многих вычислений, связанных с накоплением продуктов:

• Скалярное произведение
• Умножение матриц
• Полиномиальная оценка (например, с помощью правила Хорнера )
• Метод Ньютона для вычисления функций (по обратной функции)
• Свертки и искусственные нейронные сети
• Умножение в арифметике двойное-двойное

Обычно для получения более точных результатов можно положиться на объединенное умножение – сложение. Однако Уильям Кахан указал, что при бездумном использовании он может вызвать проблемы. Если x 2 – y 2 оценивается как (( x × x ) – y × y ) (следуя предложенной Каханом нотации, в которой избыточные круглые скобки предписывают компилятору сначала округлить член ( x × x ) ) с использованием слитного умножения – сложения, тогда результат может быть отрицательным, даже если x = y из-за того, что первое умножение отбрасывает биты с низкой значимостью. Это может привести к ошибке, если, например, вычисляется квадратный корень из результата.

При реализации внутри микропроцессора FMA может быть быстрее, чем операция умножения, за которой следует сложение. Однако стандартные промышленные реализации, основанные на оригинальной конструкции IBM RS / 6000, требуют 2 N- битного сумматора для правильного вычисления суммы.

Еще одним преимуществом включения этой инструкции является то, что она обеспечивает эффективную программную реализацию операций деления (см. Алгоритм деления ) и извлечения квадратного корня (см. Методы вычисления квадратного корня ), что устраняет необходимость в специализированном оборудовании для этих операций.

Инструкция по продукту Dot

Некоторые машины объединяют несколько слитных операций умножения и сложения в один шаг, например выполнение скалярного произведения из четырех элементов на двух 128-битных регистрах SIMDa0×b0 + a1×b1 + a2×b2 + a3×b3 с пропускной способностью за один цикл.

Служба поддержки

Операция FMA включена в IEEE 754-2008 .

Digital Equipment Corporation (DEC) VAX «s POLYинструкция используется для вычисления полиномов с правилом Горнера , используя последовательность умножения и добавить шаги. В описаниях инструкций не указывается, выполняются ли умножение и сложение с использованием одного шага FMA. Эта инструкция была частью набора инструкций VAX с момента его первоначальной реализации 11/780 в 1977 году.

Стандарт тысячи девятьсот девяносто-девять на языке программирования Си поддерживает операцию FMA через fma()стандартную функцию математической библиотеки, и стандартные псевдокомментарии ( #pragma STDC FP_CONTRACT) , управляющие оптимизации на основе FMA.

Операция слитного умножения-сложения была введена как «слияние умножения-сложения» в процессоре IBM POWER1 (1990), но с тех пор была добавлена ​​во многие другие процессоры:

• HP PA-8000 (1996) и выше
• Hitachi SuperH SH-4 (1998 г.)
• SCE – Toshiba Emotion Engine (1999)
• Intel Itanium (2001 г.)
• Ячейка ИППП (2006)
• Fujitsu SPARC64 VI (2007) и выше
• ( Совместимость с MIPS ) Loongson -2F (2008 г.)
• Эльбрус-8СВ (2018)
• процессоры x86 с набором инструкций FMA3 и / или FMA4
  • AMD Bulldozer (2011, только FMA4)
  • AMD Piledriver (2012, FMA3 и FMA4)
  • AMD Steamroller (2014)
  • Экскаватор AMD (2015)
  • AMD Zen (2017, только FMA3)
  • Intel Haswell (2013, только FMA3)
  • Intel Skylake (2015, только FMA3)
• Процессоры ARM с VFPv4 и / или NEONv2:
  • ARM Cortex-M4F (2010 г.)
  • ARM Cortex-A5 (2012 г.)
  • ARM Cortex-A7 (2013 г.)
  • ARM Cortex-A15 (2012 г.)
  • Qualcomm Krait (2012)
  • Apple A6 (2012 г.)
  • Все процессоры ARMv8
    • Fujitsu A64FX имеет «FMA с четырьмя операндами с префиксной инструкцией».
• IBM z / Architecture (с 1998 г.)
• Графические процессоры и платы GPGPU:
  • Графические процессоры Advanced Micro Devices (2009 г.) и новее
    • TeraScale 2 “Evergreen” – серия на основе
    • Графическое ядро ​​Next на базе
  • Графические процессоры NVidia (2010 г.) и новее
    • На основе

    Ферми (2010)

  • На основе Кеплера (2012)
  • Основанный на Максвелле (2014)
  • На основе Паскаля (2016)
  • Основанный на Вольте (2017)
• Графические процессоры Intel со времен Sandy Bridge
• Intel MIC (2012 г.)
• ARM Mali T600 Series (2012) и выше

• Векторные процессоры:
  • NEC SX-Aurora TSUBASA

• Рекомендации

Источник

У микроконтроллеров AVR, по сути, имеется два пути реализации умножения, разница между которыми заключается в форме представления произведения и, соответственно, в различии выполняемых арифметических операций. Первый оптимизирован для использования с командой однобайтового умножения, второй – использует только сложение и сдвиговые операции. Для произведения n-разрядного множимого и m-разрядного множителя необходимо отводить n+m разрядов.

Помимо этого существует особый случай умножения на целую степень 2. Всё дело в том, что 2 является основанием двоичной системы, а в любой позиционной системе операция умножения числа на основание системы приводит к увеличению веса каждого его разряда на порядок:

2*X = 2*(xn-1*2n-1 + xn-2*2n-2 + … + x1*21 + x0*20) = xn-1*2n + xn-2*2n-1 + … + x1*22 + x0*21­­.

Как видно, коэффициенты xn числа X переместились на один разряд влево (x0 стал при 21, x1 стал при 22 и т.д.). Итак, для умножения двоичного числа на 2n необходимо просто сдвинуть его на n разрядов влево. Так можно осуществить умножение на 2 двухбайтового числа в регистрах R17:R16 посредством сдвиговых операций:

lsl R16 ;R16 <- R16 << 1 (LSB <- 0, флаг С <- MSB) rol R17 ;R17 <- R17 << 1 (LSB <- флаг С, флаг С <- MSB)

Тот же результат можно получить, складывая число с самим собой:

add R16, R16 adc R17, R17

Благодаря тому, что операции сдвига и сложения выполняются за одинаковое время (1 машинный цикл) оба примера равноценны.

Иногда встречаются операции умножения на число, которое близко к степени 2. В таких случаях намного проще заменить его суммой двух слагаемых, одно из которых кратно 2n, и использовать только операции сдвига и сложения (вычитания):

63*X = (26-1)*X = 26*X – X = X<<6 – X,

33*X = (25+1)*X = 25*X + X = X<<5 + X,

130*X = (27+2)*X = 27*X + 2*X = X<<7 + X<<2.

Для умножения 2-байтовых чисел (обозначим их как XH:XL = 28*XH + XL и YH:YL = 28*YH + YL) применяется следующая вычислительная схема:

XH:XL * YH:YL = (28*XH + XL)*(28*YH + YL) = 216*XH*YH + 28*(XH*YL + YH*XL) + XL*YL.

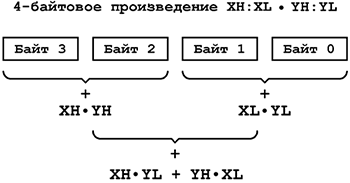
Рис.1 Вычислительная схема для умножения двухбайтовых чисел с использованием инструкции умножения

Отыскание 32-разрядного результата сводится к последовательности операций однобайтовых умножений и последующего сложения всех произведений с учётом сдвига слагаемых XH*YL, XL*YH на 1 байт и XH*YH на 2 байта, как показано на рис.1. Подпрограмма, реализующая эти действия, приведена ниже. Напомним, что произведение двух однобайтовых множителей, полученное в результате выполнения команды mul Rd,Rr или любой другой команды умножения, всегда заносится в регистровую пару R1:R0.

; R23:R22:R21:R20 = R17:R16 * R19:R18 ; R23:R22:R21:R20 – произведение ; R17:R16 – множимое ; R19:R18 – множитель ; R1,R0 – вспомогательные регистры mul16_16: mul R16,R18 ;находим XL*YL = R16*R18 и заносим его в movw R20,R0 ;младшие байты произведения R21:R20 mul R17,R19 ;находим XH*YH = R17*R19 и заносим его в movw R22,R0 ;старшие байты произведения R23:R22 mul R17,R18 ;находим XH*YL = R17*R18 и прибавляем его к clr R17 ;байтам R23:R22:R21 произведения add R21,R0 adc R22,R1 adc R23,R17 mul R16,R19 ;находим YH*XL = R19*R16 и прибавляем его к add R21,R0 ;байтам R23:R22:R21 произведения adc R22,R1 adc R23,R17 ret

Возвести двухбайтовое число в квадрат еще проще:

XH:XL * XH:XL = (28*XH + XL)*(28*XH + XL) = 216*XH*XH + 28*2*XH*XL + XL*XL.

Подпрограмма возведения в квадрат приведена ниже. Она является хорошим примером того, где может пригодиться инструкция fmul Rd,Rr, которая одним действием производит умножение двух однобайтовых чисел и сдвиг произведения на 1 разряд влево.

; R21:R20:R19:R18 = R17:R16 * R17:R16 ; R17:R16 – число, возводимое в квадрат ; R21:R20:R19:R18 – произведение ; R1,R0 – вспомогательные регистры sqr16_16: mul R16,R16 ;находим XL*XL = R16*R16 и заносим его в movw R18,R0 ;младшие байты произведения R19:R18 mul R17,R17 ;находим XH*XH = R17*R17 и заносим его в movw R20,R0 ;старшие байты произведения R21:R20 fmul R17,R16 ;находим 2*XH*YL = R17*R18 и прибавляем его clr R17 ;к байтам R21:R20:R19 произведения rol R17 add R19,R0 adc R20,R1 adc R21,R17 ret

Во многих случаях команда fmul Rd,Rr позволяет использовать аппаратный умножитель 8×8 фактически как умножитель 9×8 с получением 17-разрядного результата (MSB произведения размещается в C). Это бывает очень полезно, когда возникает необходимость умножить переменную на постоянный числовой коэффициент, который немного выходит за пределы 8-разрядной сетки. Так, допустим, можно умножить число из R16 на 500

ldi R17,250 ;R1:R0 <- (250<<1)*R16 = 500*R16 fmul R17,R16 ; флаг С <- MSB

или на 1000:

ldi R17,250 ;R1:R0 <- (250<<2)*R16 = 1000*R16 fmul R17,R16 ;флаг С <- MSB lsl R0 rol R1

Ниже показан другой практически важный пример умножения, когда один из множителей (множитель X) однобайтовый. В основе подпрограммы лежит следующая вычислительная схема:

X * YH:YL = X*(28*YH + YL) = 28*X*YH + X*YL

; R21:R20:R19 = R18 * R17:R16 ; R21:R20:R19 – произведение ; R18 – множимое ; R17:R16 – множитель ; R1,R0 – вспомогательные регистры mul8_16: mul R18,R17 ;находим X*YH = R18*R17 и заносим его в movw R20,R0 ;старшие байты произведения R21:R20 mul R18,R16 ;находим X*YL = R18*R16 clr R18 add R19,R0 ;и прибавляем его add R20,R1 ;к произведению R21:R20:R19 adc R21,R18 ret

Точно также могут быть разложены числа и с большей разрядностью. Однако с ростом их величины начинают резко возрастать и затраты ресурсов процессора. Так для умножения трёхбайтовых чисел понадобится по 9 операций однобайтовых умножений и двухбайтовых сложений; для четырёхбайтовых уже по 16 операций и т.д.

В подобных случаях необходимо использовать другой, наиболее общий алгоритм, который не использует команду mul Rd,Rr. А для микроконтроллеров семейства ATtiny, (а также для устаревшей линейки моделей Classic), у которых отсутствует аппаратный умножитель, он вообще является единственно возможным.

Для пояснения алгоритма, перепишем произведение Z двух произвольных двоичных чисел

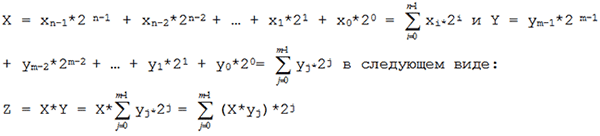
Произведение X*yj называется частичным произведением (X*yj = X при yj =1 и X*yj = 0 при yj =0), а произведение (X*yj)*2j есть не что иное, как частичное произведение, сдвинутое на j разрядов влево. Итак, нахождение произведение X*Y сводится к нахождению суммы частичных произведений X*yj, каждое из которых в свою очередь сдвинуто на j разрядов влево соответственно. На этом принципе основан школьный метод умножения в столбик. Рассмотрим пример умножения двух 4-разрядных чисел:

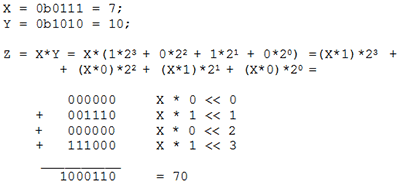
Как видим, для получения результата используются только операции сложения и сдвига. При этом в тех разрядах Y, где yj=0 и X*yj=0. И если предварительно анализировать значения yj/, то можно пропускать пустое сложение с 0 в соответствующих итерациях. Ниже приведена подпрограмма умножения двух трёхбайтовых чисел. В ней для получения суммы частичных произведений, сдвинутых каждое на j разрядов влево, производится сдвиг накопителя произведений m=24 раза вправо, а для экономии памяти младшие 3 байта произведения заносятся в те же регистры, где находился множитель.

; R24:R23:R22:R21:R20:R19 = R18:R17:R16 * R21:R20:R19 ; R24:R23:R22:R21:R20:R19 – произведение ; R18:R17:R16 – множимое ; R21:R20:R19 – множитель ; R25,R1,R0 – вспомогательный регистр mul24_24: clr R22 ;очищаем регистры R22,R23,R24 clr R23 ;при входе в подпрограмму clr R24 ldi R25,24 ;инициализируем счётчик циклов сложения clc ;сдвинутых частичных произведений ml1: sbrs R19,0 ;если младший бит множителя 1, то rjmp ml2 add R22,R16 ;добавляем к накопителю очередное adc R23,R17 ;частичное произведение R18:R17:R16 adc R24,R18 ml2: ror R24 ;байтам R24:R23:R22 накопителя произведения ror R23 ;в ином случае пропускаем это действие ror R22 ;и переходим к очередному сдвигу множителя ror R21 ror R20 ror R19 clc dec R25 ;повторяем m=24 раз цикл сложения brne ml1 ;сдвинутых частичных произведений ret

Перейти к следующей части: Деление

Теги:

Источник