Разложение перестановки в произведение независимых циклов
В теории групп циклическая перестановка – это перестановка элементов некоторого множества X, которая переставляет элементы некоторого подмножества S множества X циклическим образом, сохраняя на месте остальные элементы X (т.е. отображая их в себя). Например, перестановка {1, 2, 3, 4}, переводящая 1 в 3, 3 в 2, 2 в 4 и 4 в 1 является циклической, в то время как перестановка, переводящая 1 в 3, 3 в 1, 2 в 4 и 4 в 2 циклической не является.
Цикл в перестановке – это подмножество элементов, которые переставляются циклическим образом. Множество S называется орбитой цикла. Каждую перестановку конечного множества элементов можно разложить в объединение циклов с непересекающимися орбитами. В некоторых контекстах циклическая перестановка сама по себе называется циклом.
Определение[править | править код]
Перестановка называется циклической тогда и только тогда, когда она состоит из единственного нетривиального цикла (т.е. цикла длиной больше 1)[1].
Пример:
Некоторые авторы ограничивают определение только теми перестановками, которые имеют в точности один цикл (то есть, не разрешаются перестановки, имеющие фиксированные точки[2].
Пример:
Более формально, перестановка множества X, которая является биективной функцией , называется циклической, если действие на X подгруппы с генератором имеет максимум одну орбиту из более чем одного элемента[3]. Это понятие чаще всего используется, когда X является конечным множеством. Тогда, конечно, наибольшая орбита S также конечна. Пусть – любой элемент S, положим для любого . Если множество S конечно, имеется минимальное число , для которого . Тогда и является перестановкой, определённой формулой
для
и для любого элемента . Элементы, не фиксируемые отображением , можно представить как
.
Цикл можно записать с использованием компактной циклической записи (запятая между элементами в такой записи не ставится, чтобы избежать путаницы с кортежами). Длина цикла – это число элементов его наибольшей орбиты. В циклической записи циклы длины 1 часто опускаются, если это не вызывает путаницы[4].
Основные свойства[править | править код]
По одному из основных свойств симметрических групп, любую перестановку можно представить как произведение непересекающихся циклов (более точно – циклов с непересекающимися орбитами). Такие циклы можно переставлять друг с другом, и выражение перестановки единственно с точностью до порядка циклов (заметим, что циклическая запись не единственна – любой k-цикл сам по себе может быть записан k различными способами в зависимости от выбора в его орбите). Мультимножество длин циклов (цикловый тип) однозначно определяется перестановкой.
Число различных циклов длины k в симметрической группе Sn задаётся для следующей формулой
Цикл длины k имеет чётность (−1)k − 1.
Транспозиции[править | править код]
Цикл, состоящий из двух элементов, называется транспозицией. Например, перестановка {1, 4, 3, 2}, переводящая 1 в 1, 2 в 4, 3 в 3 и 4 в 2 является транспозицией (а именно, транспозицией, переставляющей 2 и 4).
Любую перестановку можно представить как композицию (произведение) транспозиций – формально, они являются генераторами группы[5]. Более того, любую перестановку упорядоченного множества X = {1, 2, …, n} можно выразить как произведение смежных транспозиций, то есть транспозиций вида Действительно, любую транспозицию можно представить в виде произведения смежных транспозиций.
Разложение перестановки в произведение транспозиций можно получить, например, путём выписывания перестановки как произведения различных циклов, а затем итеративного разложения циклов длины 3 и более в произведение транспозиции и цикла на единицу короче:
Симметрическая группа является группой Коксетера, в том смысле, что она порождается элементами порядка 2 (смежными транспозициями) и все соотношения имеют определённый вид.
Один из главных результатов элементарной теории симметрических групп утверждает, что либо все разложения данной перестановки на транспозиции имеют чётное число транспозиций, либо все разложения имеют нечётное число транспозиций[6]. Это позволяет чётности перестановки быть хорошо определённой функцией.
См. также[править | править код]
- Циклическая сортировка[en] – алгоритм сортировки, основанный на идее, что массив можно разложить на циклы, которые можно индивидуально прокрутить, чтобы получить сортированный массив
- Циклы и фиксированные точки[en]
- Циклические перестановки целых чисел[en]
- Циклические перестановки в протеинах[en]
Примечание[править | править код]
- ↑ Bogart, 1990, с. 486.
- ↑ Gross, 2008, с. 29.
- ↑ Fraleigh, 1993, с. 103.
- ↑ Sagan, 1991, с. 2.
- ↑ Rotman, 2006, с. 118, Prop. 2.35.
- ↑ Rotman, 2006, с. 122.
Литература[править | править код]
- Anderson M., Feil T. . A First Course in Abstract Algebra. 2nd edition. – Boca Raton: Chapman & Hall/CRC, 2005. – 696 p. – ISBN 1-58488-515-7.
- Fraleigh J. . A First Course in Abstract Algebra. 5th edition. – Reading: Addison-Wesley, 1993. – 576 p. – ISBN 978-0-201-53467-2.
- Rotman J. J. . A First Course in Abstract Algebra with Applications. 3rd edition. – Upper Saddle River: Prentice Hall, 2006. – 581 p. – ISBN 978-0-13-186267-8.
- Sagan B. E. . The Symmetric Group: Representations, Combinatorial Algorithms & Symmetric s. – Belmont: Wadsworth, 1991. – 197 p. – ISBN 978-0-534-15540-7.
- Bogart K. P. . ductory Combinatorics. 2nd edition. – San Diego: Harcourt, Brace, Jovanovich, 1990. – 622 p. – ISBN 0-15-541576-X.
- Gross J. L. . Combinatorial Methods with Computer Applications. – Boca Raton: Chapman & Hall/CRC, 2008. – xvii + 644 p. – ISBN 978-1-58488-743-0.
Ссылки[править | править код]
- Permutations as a Product of Transpositions
Источник
Выясним, как “ведет себя” перестановка в области определения. Рассмотрим произвольную перестановку 
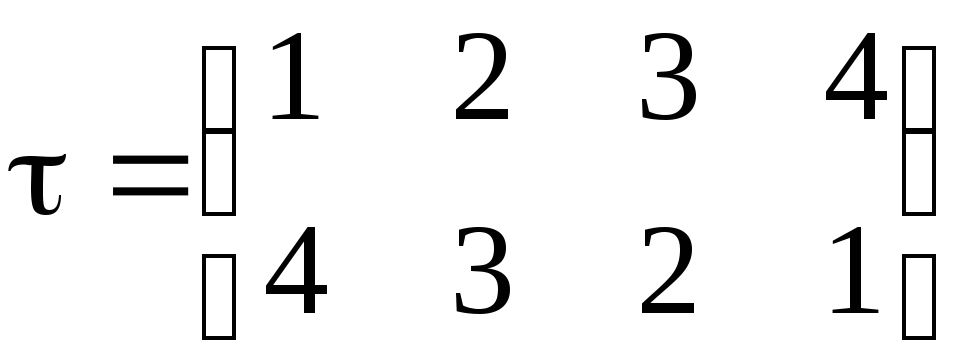 .
.
Эта перестановка переводит единицу в четверку, четверку в единицу, двойка переходит в тройку, а тройка в двойку.
Если все перечисленные замены записать в той последовательности, в которой мы их производили, то рассматриваемая перестановка примет вид:
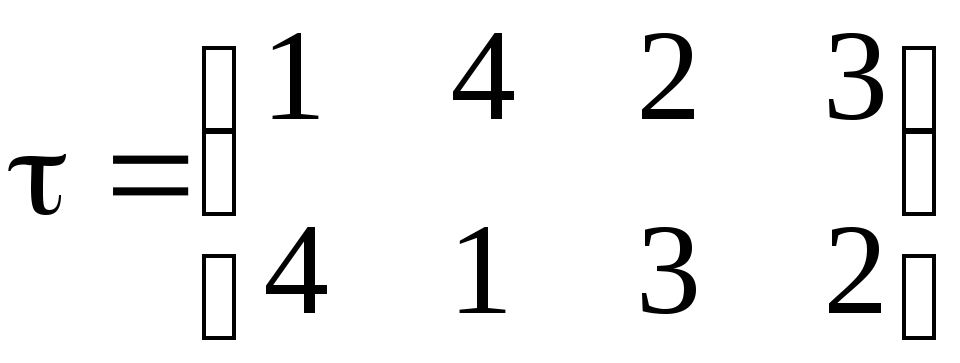 .
.
Нетрудно заметить, что перестановка оказалась, по существу, разложенной на две части.
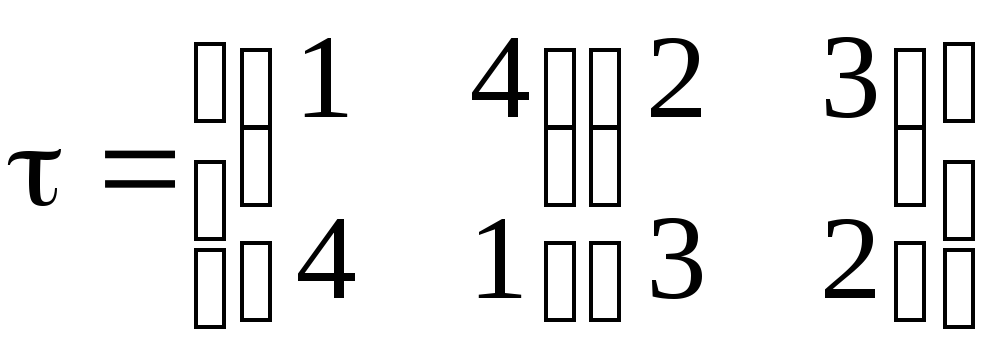 .
.
Это означает, что наша перестановка состоит из двух независимых частей, каждая из которых перемещает элементы, принадлежащие её собственной области определения (рис. 1).
Рис. 1 – Разложение перестановки  .
.
Именно потому, что обе части перестановки независимы, совершенно безразлично, какую из перестановок
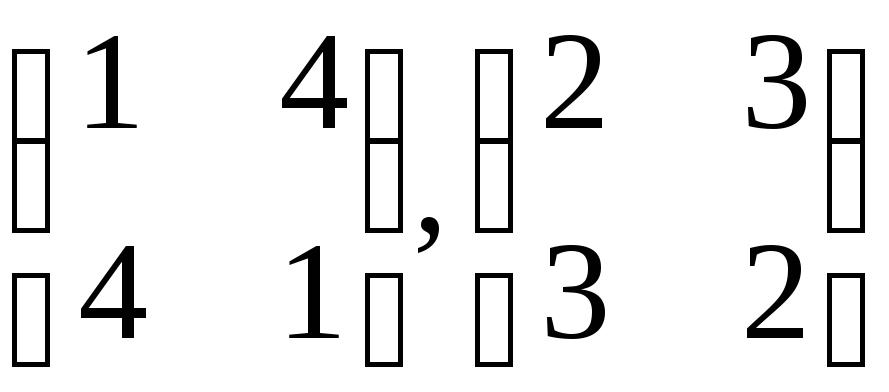
выполнять первой, а какую второй. Если перестановки
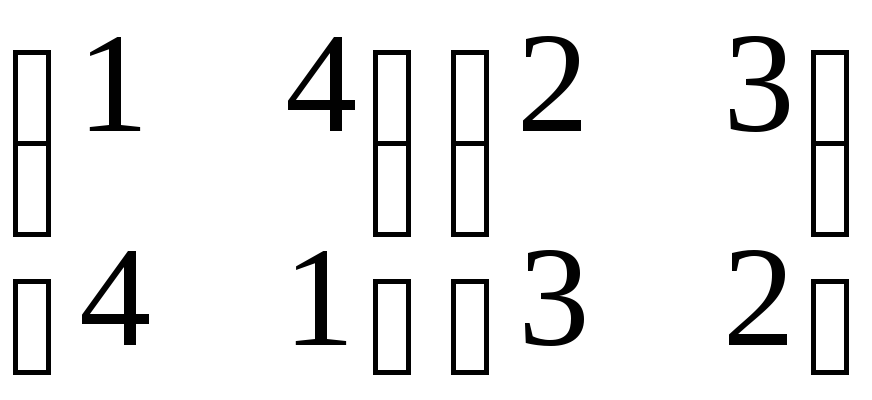
выполнять последовательно одну за другой, то такие действия можно рассматривать, как умножение перестановок. Однако до сих пор мы говорили об умножении перестановок в тех случаях, когда области определения перестановок совпадали. Здесь же области определения перестановок различны.
Преодолеть возникшую проблему не составляет труда: условимся считать, что наши перестановки переводят каждый “недостающий” элемент в самого себя.
Таким образом, перестановка допускает следующее разложение в произведение двух независимых перестановок:
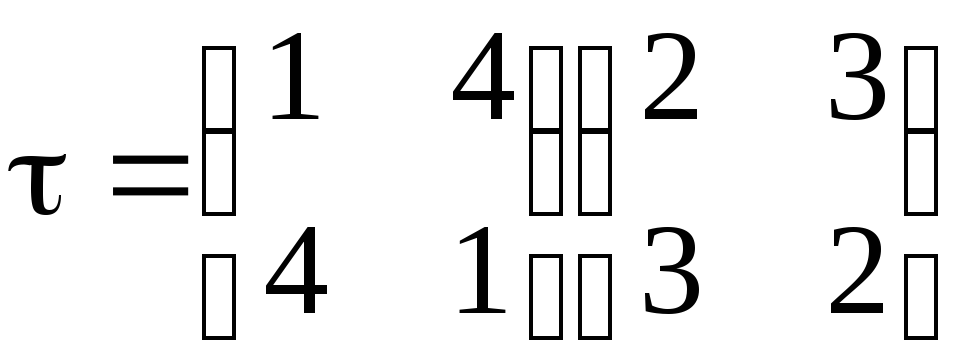 .
.
Легко заметить, что в данном разложении нижние строки совершенно излишни. Действительно, верхние строки состоят из тех же элементов, что и нижние, причем каждый элемент под действием перестановки переходит в следующий. Это позволяет представить нашу перестановку в виде
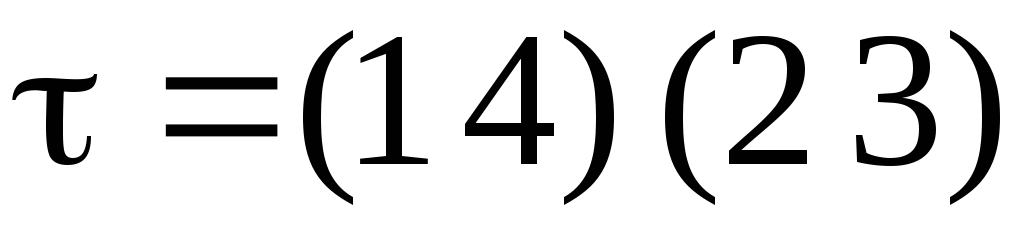 .
.
Перестановки, стоящие в правой части, называются независимыми циклами, а представление перестановки
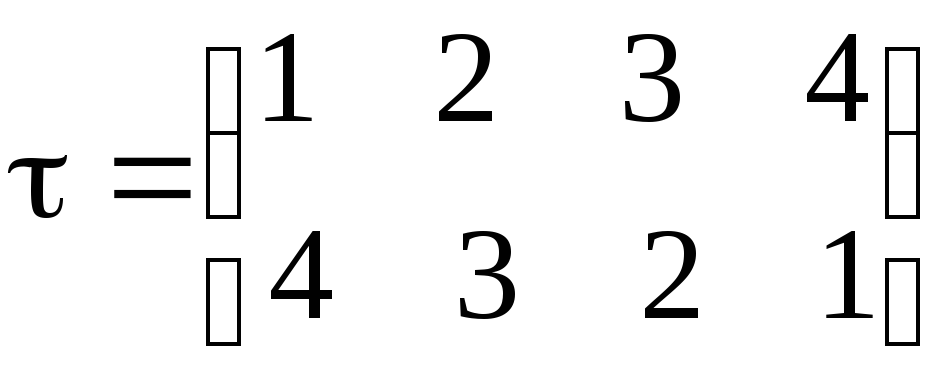
в виде
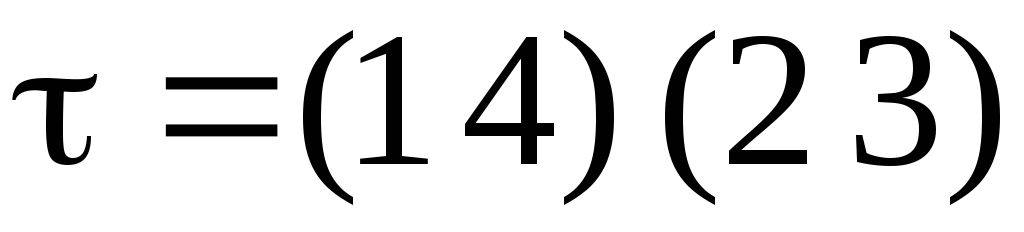
называется разложением перестановки  в произведение независимых циклов.
в произведение независимых циклов.
Определение. Длиной цикла называется количество входящих в него элементов (в данном случае циклы имеют длину, равную двум).
Перестановка
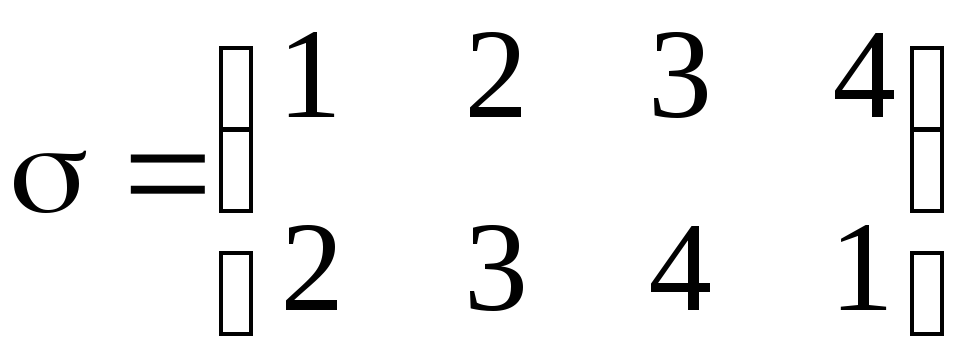
допускает разложение только в один цикл
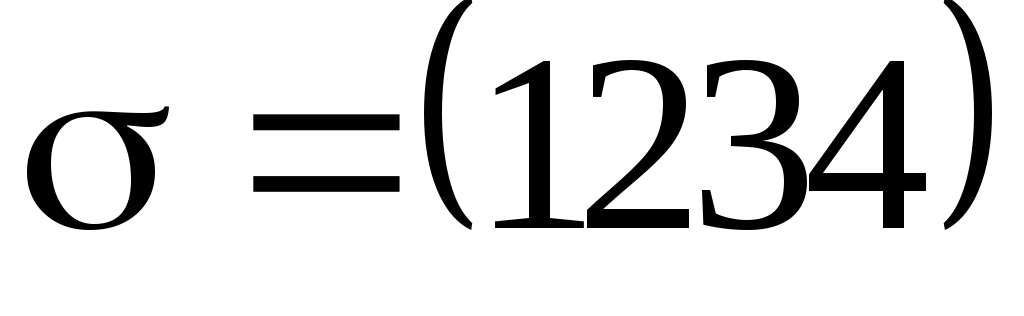
длиной 4.
Разложение перестановки в произведение независимых циклов эквивалентно разбиению множества на непересекающиеся классы
, где 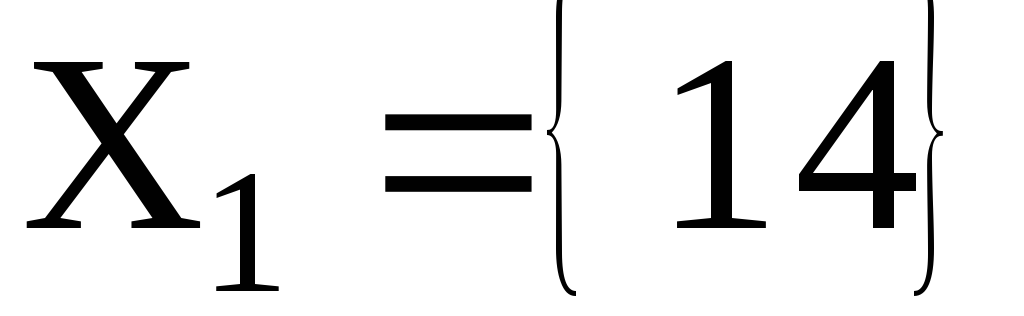 ,
,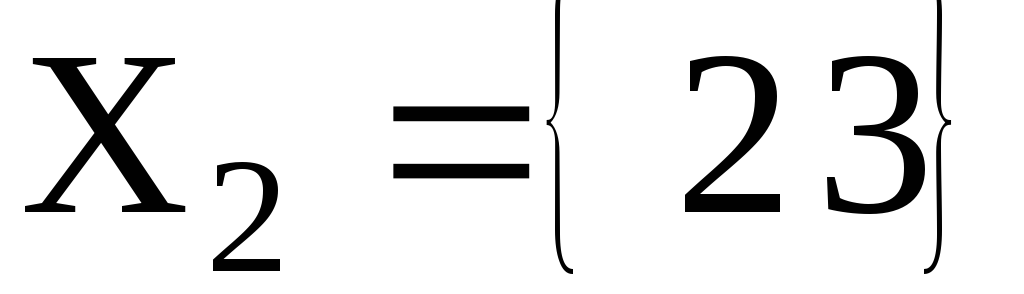 .
.
Известно, что разбиение множества на непересекающиеся классы эквивалентно введению некоторого отношения эквивалентности. Элементы, входящие в один из циклов, являются эквивалентными между собой, а сами циклы представляют собой классы эквивалентности.
Если  некоторая перестановка, определенная на множестве
некоторая перестановка, определенная на множестве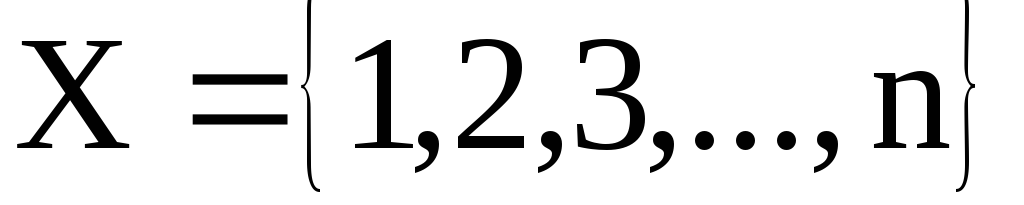 , которую можно представить в виде произведения независимых циклов
, которую можно представить в виде произведения независимых циклов
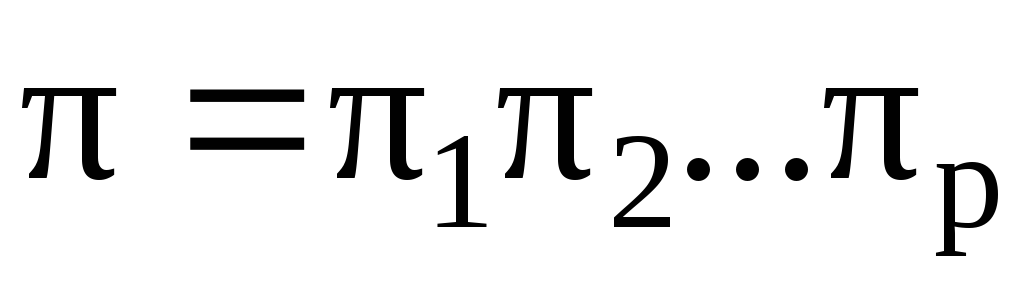 ,
,
то элементы множества можно представить в виде объединения р попарно непересекающихся подмножеств
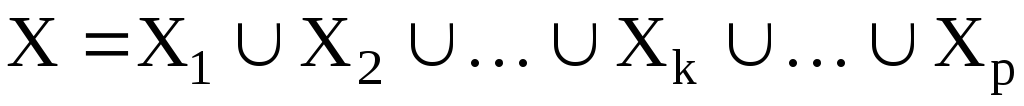 .
.
Таких, что
.
Множества 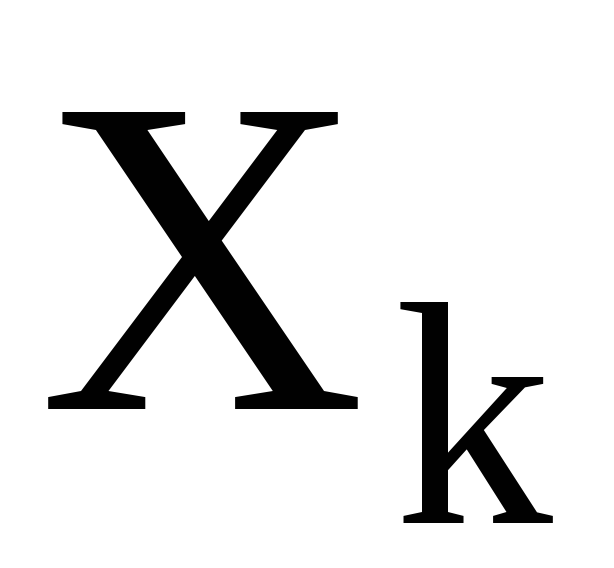 называются-орбитами. Название это вполне обоснованно. Каждая точка
называются-орбитами. Название это вполне обоснованно. Каждая точка 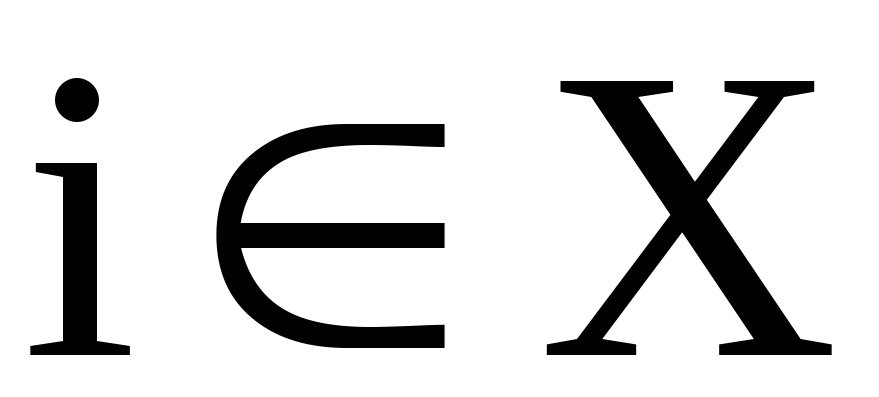 принадлежит в точности одному классу эквивалентности, например
принадлежит в точности одному классу эквивалентности, например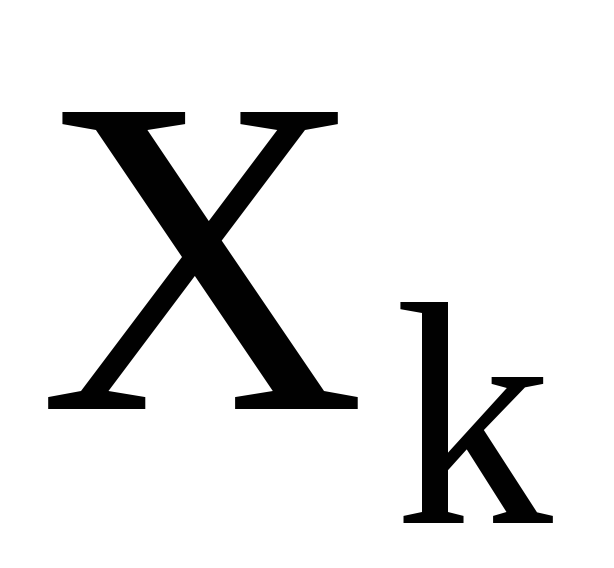 или
или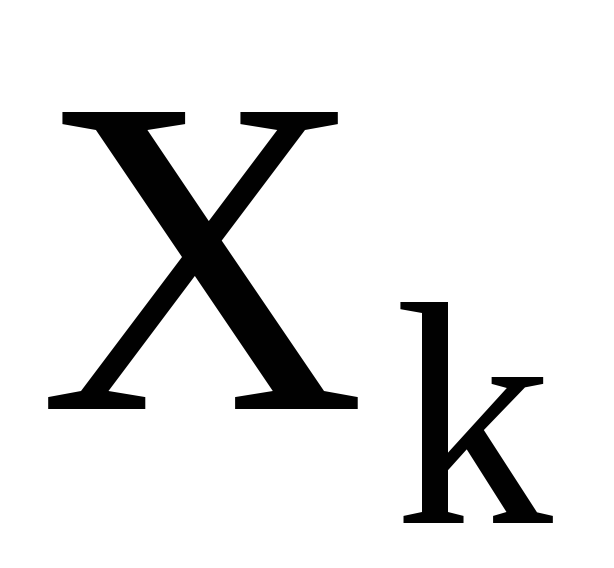 – орбите.
– орбите.
Если 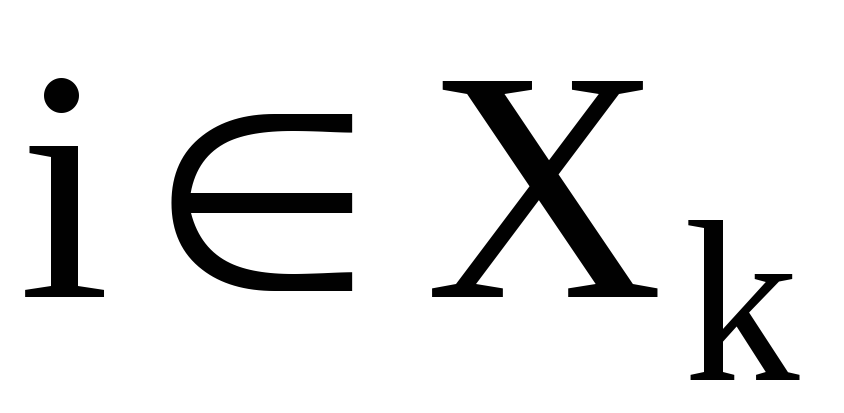 , то
, то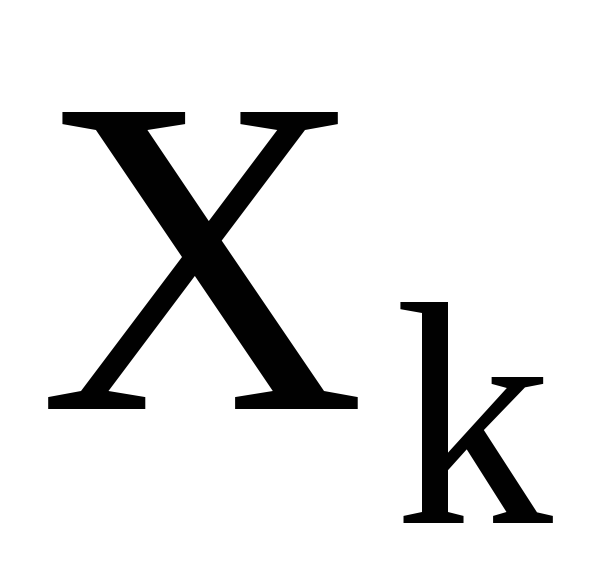 состоит из образов точки i при действии степеней элемента
состоит из образов точки i при действии степеней элемента
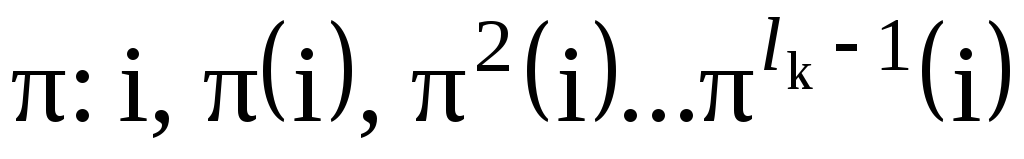 ,
,
где 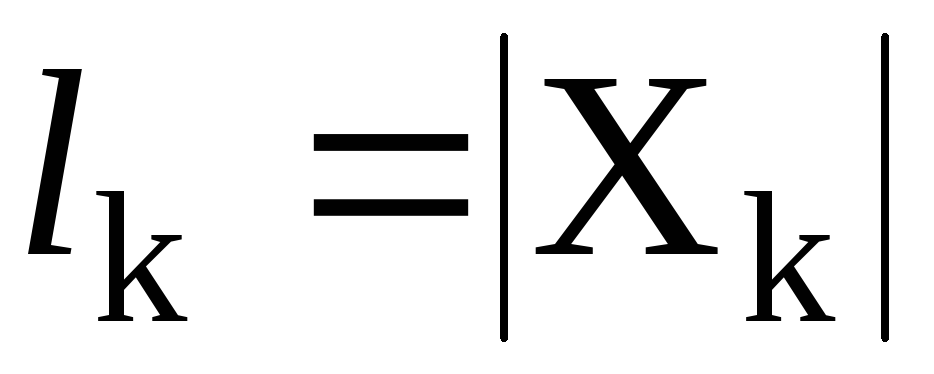 – длина k-го цикла орбиты
– длина k-го цикла орбиты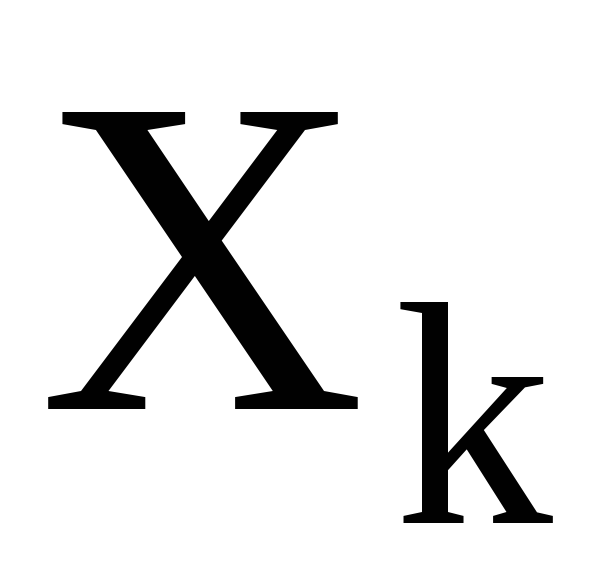 . Очевидно, что
. Очевидно, что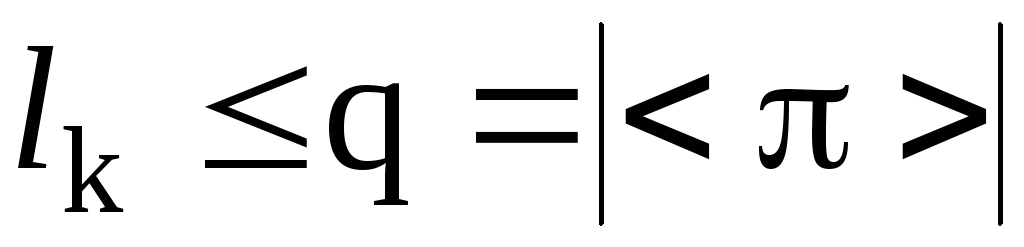 и
и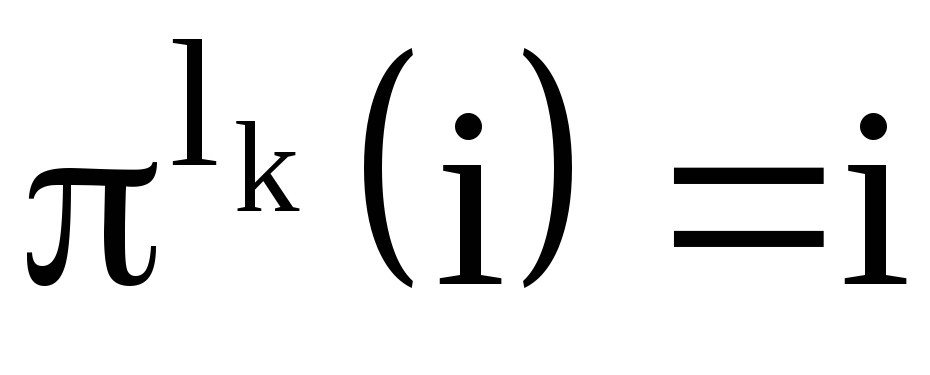 , причем
, причем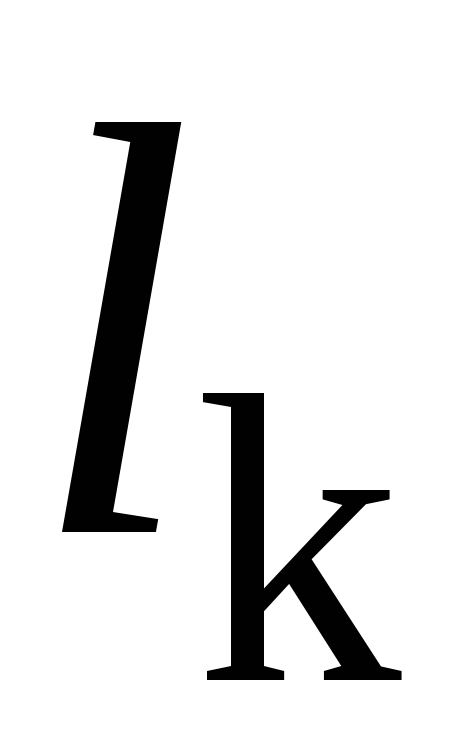 – наименьшее число, обладающее этим свойством.
– наименьшее число, обладающее этим свойством.
Цикл 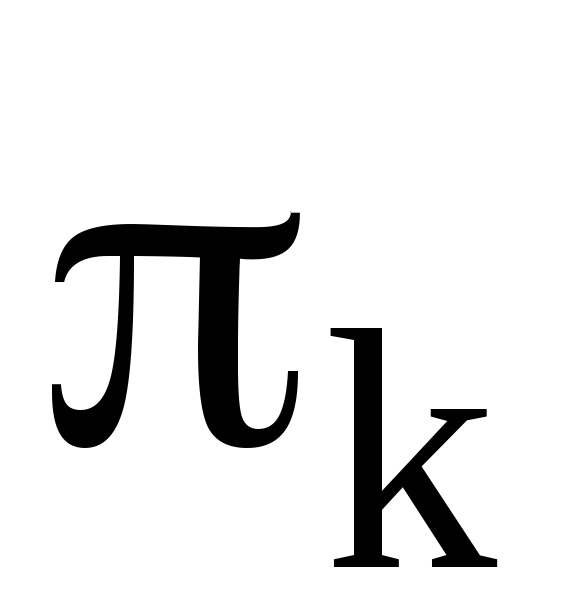 можно представить в виде:
можно представить в виде:
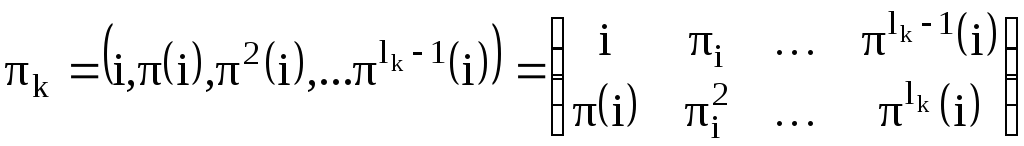 . (4)
. (4)
Цикл k оставляет на месте все точки из множества 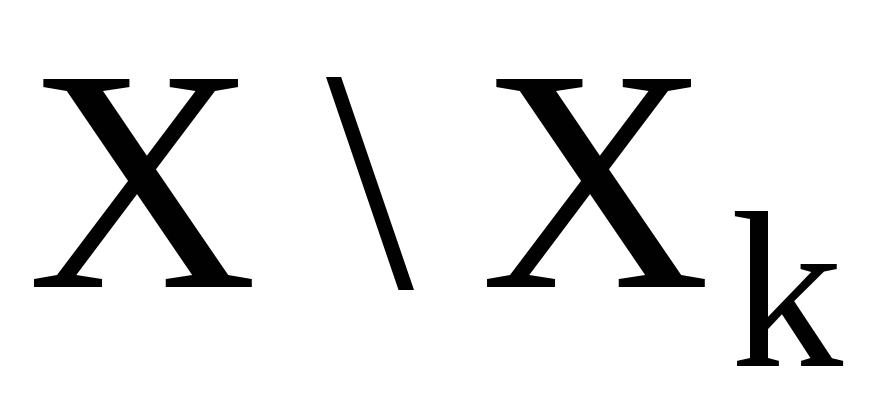 , а для любой точки
, а для любой точки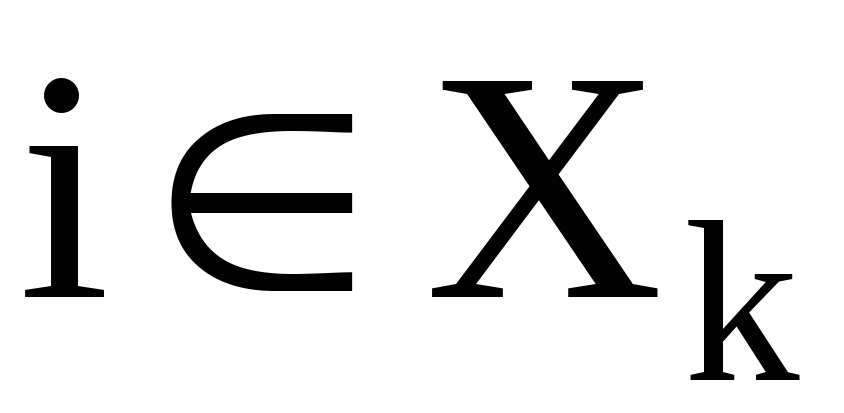
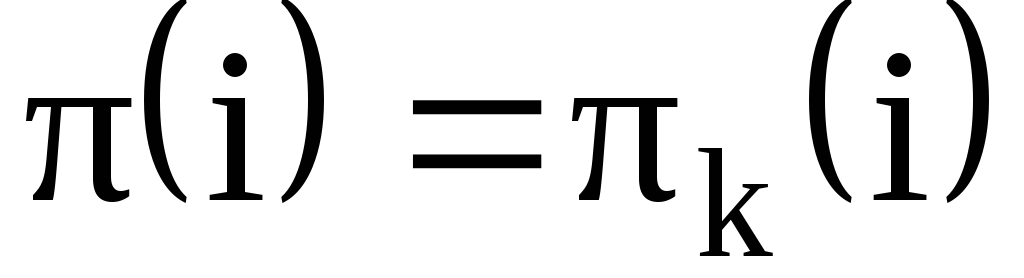 (5)
(5)
Это свойство дает нам основание называть циклы 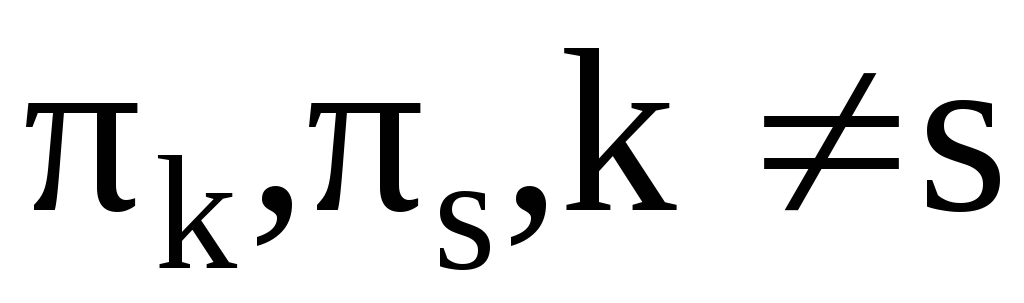 независимыми или непересекающимися циклами.
независимыми или непересекающимися циклами.
Теорема. Каждая перестановка 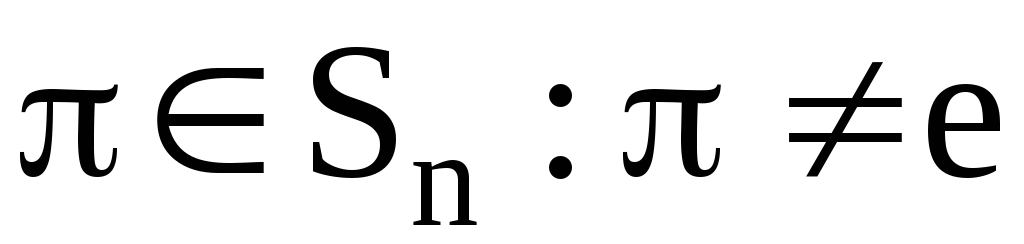 может быть представлена в виде произведения
может быть представлена в виде произведения независимых циклов длины
независимых циклов длины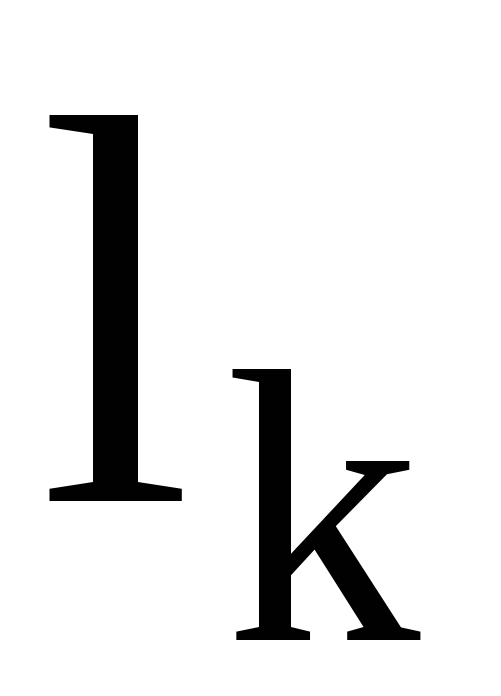
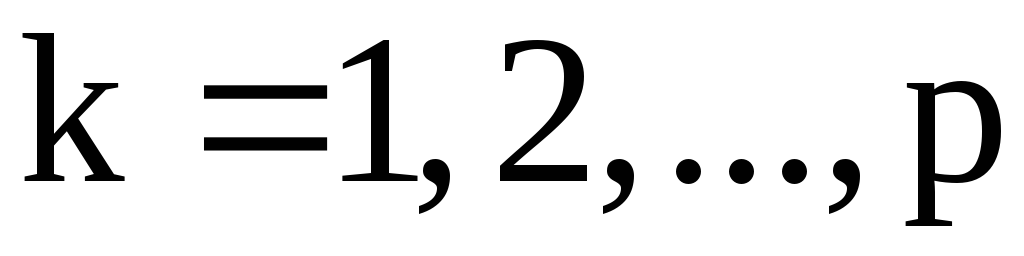 . Это разложение определено однозначно с точностью до порядка следования циклов.
. Это разложение определено однозначно с точностью до порядка следования циклов.
. (6)
Замечание. Длина каждого k-го цикла – 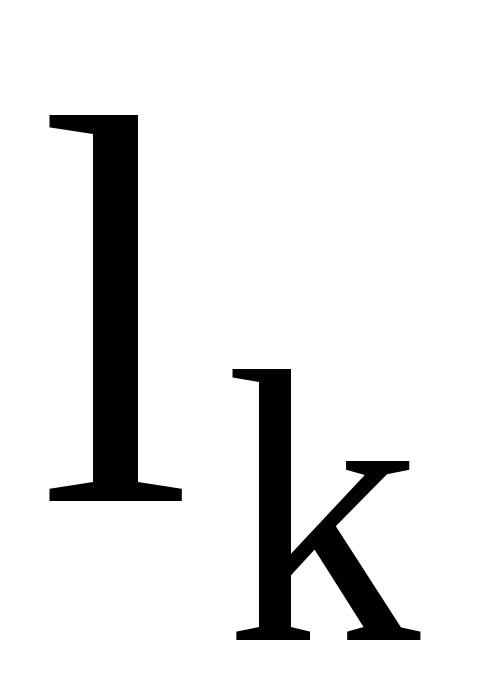 ,больше или равна двум. Если цикл
,больше или равна двум. Если цикл имеет длину равную единице, то он действует как единичная перестановка и его в произведении (5) естественно опускать.
имеет длину равную единице, то он действует как единичная перестановка и его в произведении (5) естественно опускать.
Например, перестановку

можно представить в виде
.
Запись перестановки в виде произведения независимых циклов (5) позволяет легко найти порядок перестановки
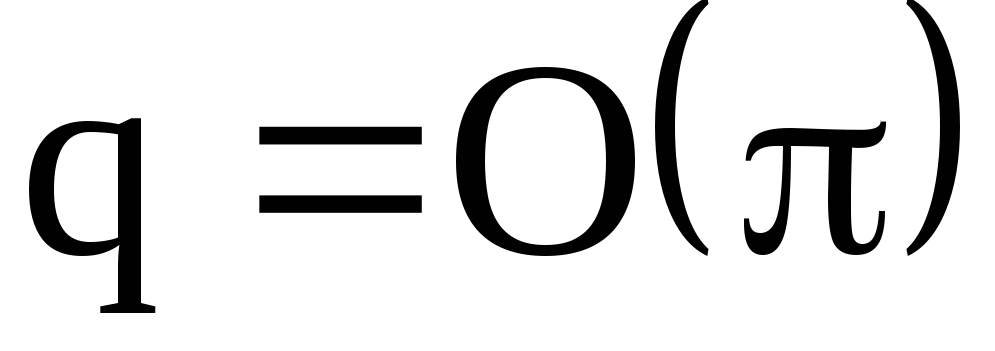 .
.
Следствие 1. Порядок 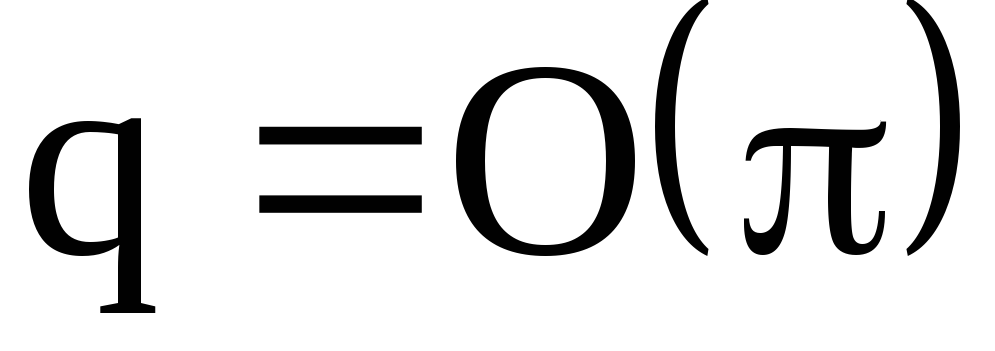 перестановки
перестановки (порядок циклической подгруппы
(порядок циклической подгруппы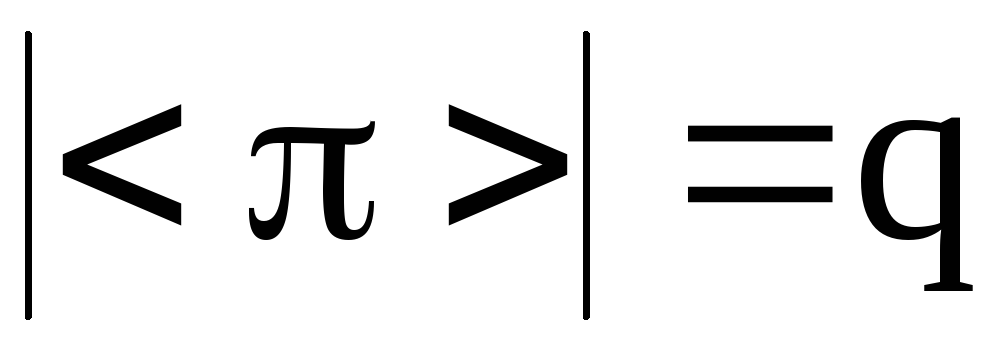 ) равен наименьшему общему кратному (НОК) длин независимых циклов, входящих в разложение.
) равен наименьшему общему кратному (НОК) длин независимых циклов, входящих в разложение.
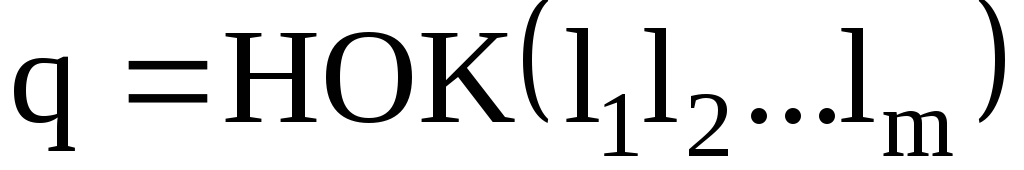
Доказательство. Представим перестановку  в виде произведения независимых циклов
в виде произведения независимых циклов
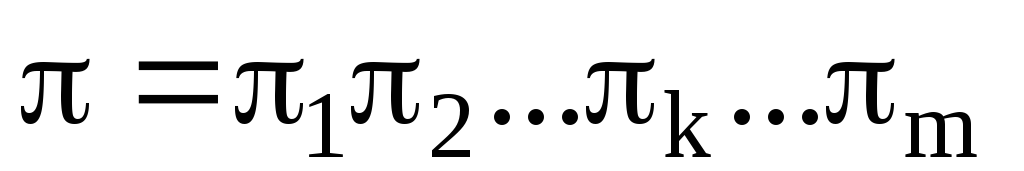 . (7)
. (7)
Тогда
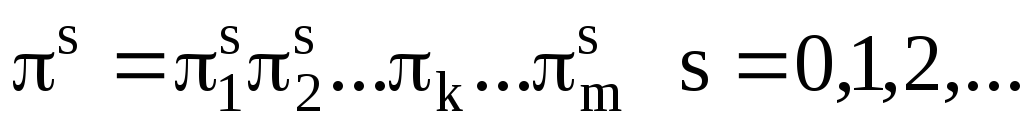
Так как циклы 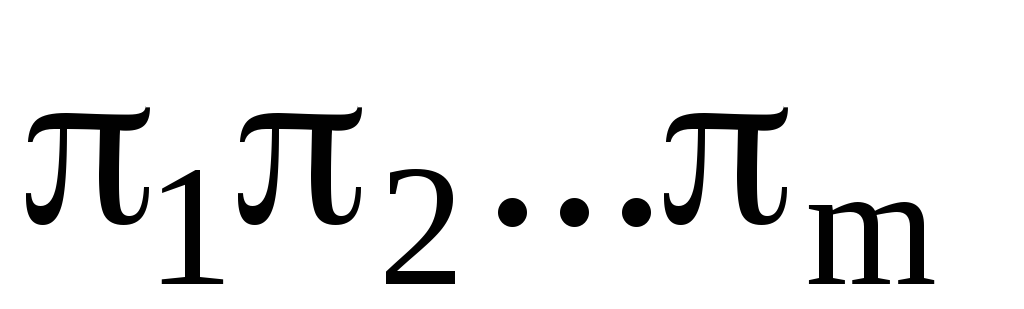 независимы (они действуют на различных множествах
независимы (они действуют на различных множествах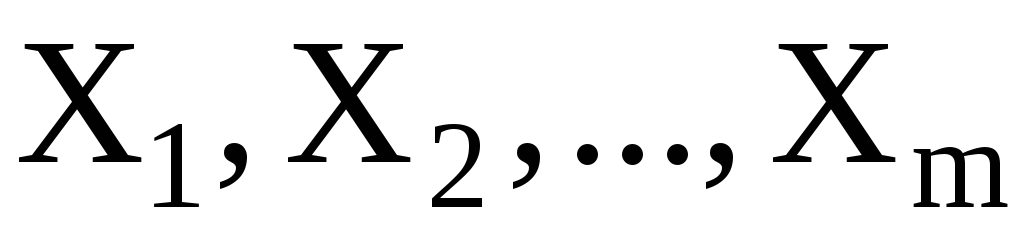 ), и если q – порядок циклической подгруппы,
), и если q – порядок циклической подгруппы,
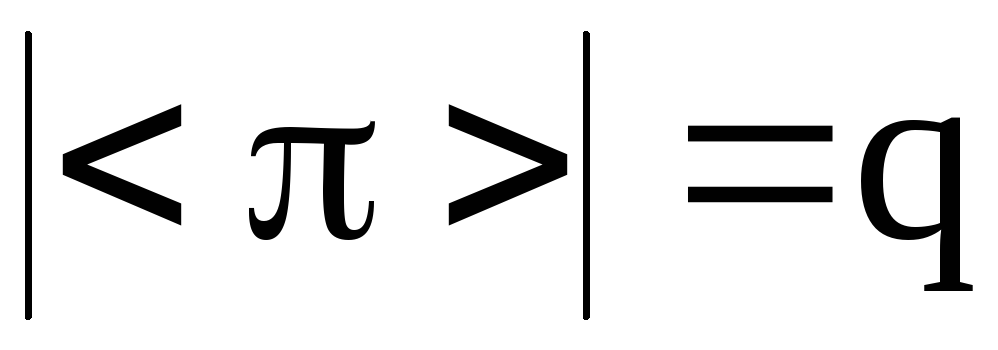 ,
,
то
 ,
,
где 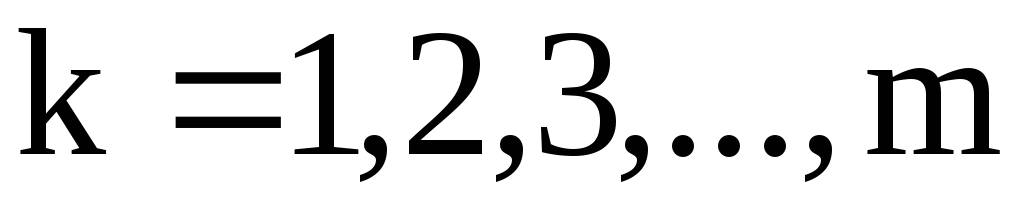 .
.
Следовательно, q – общее кратное порядков циклов k, которые совпадают с их длинами 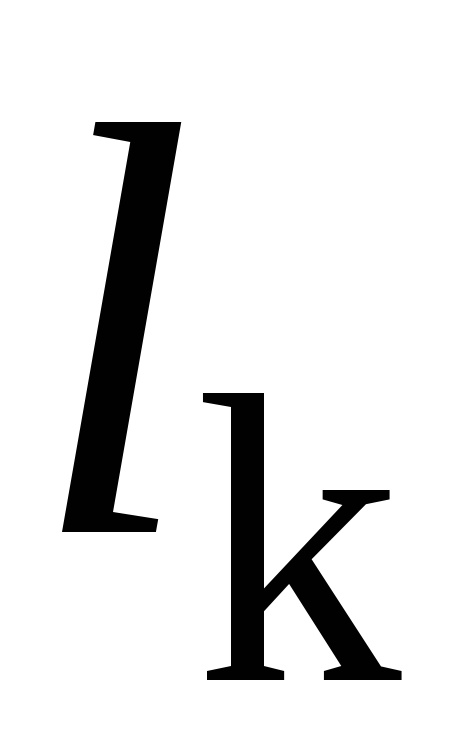 .
.
Если q – наименьшее положительное число, для которого
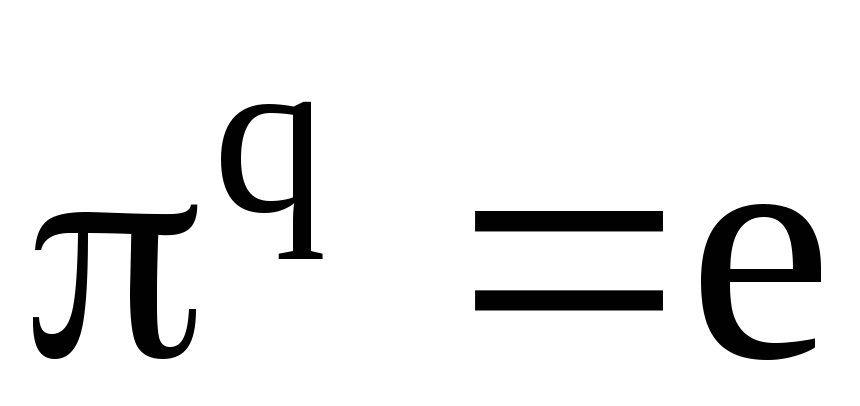 ,то
,то 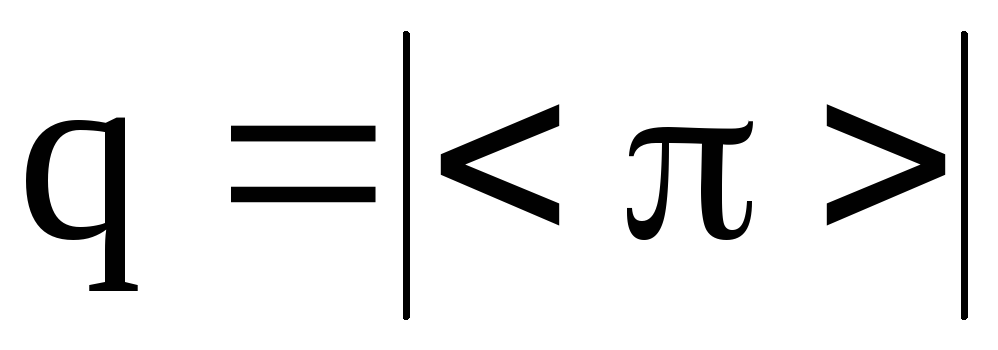
и
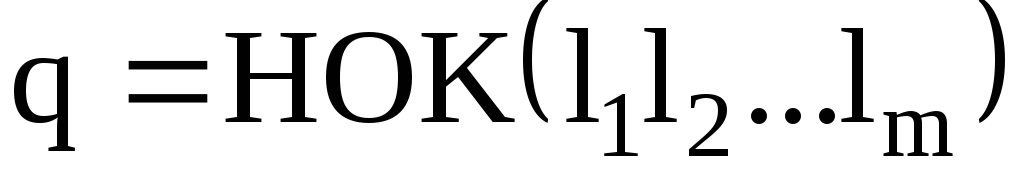 . (8)
. (8)
Замечание. Два любых целых числа m и n можно записать в виде произведений одних и тех же простых чисел
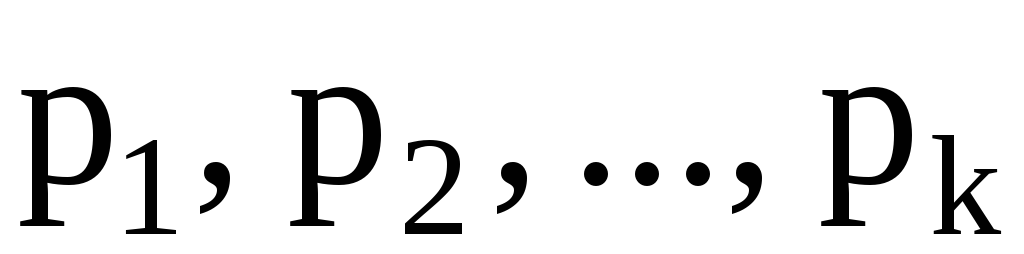 .
.
Например
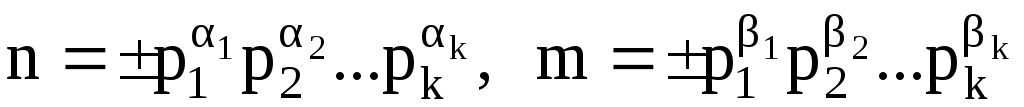 ,
,
тогда
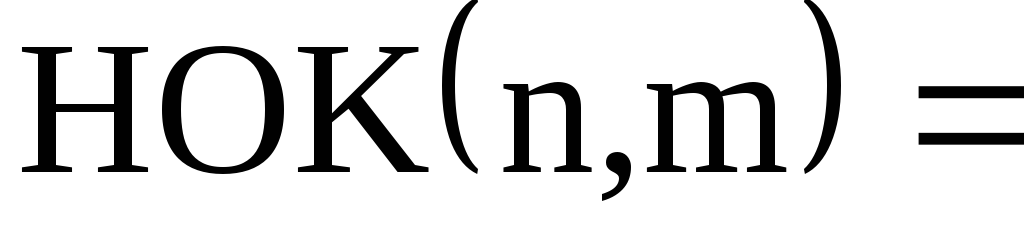
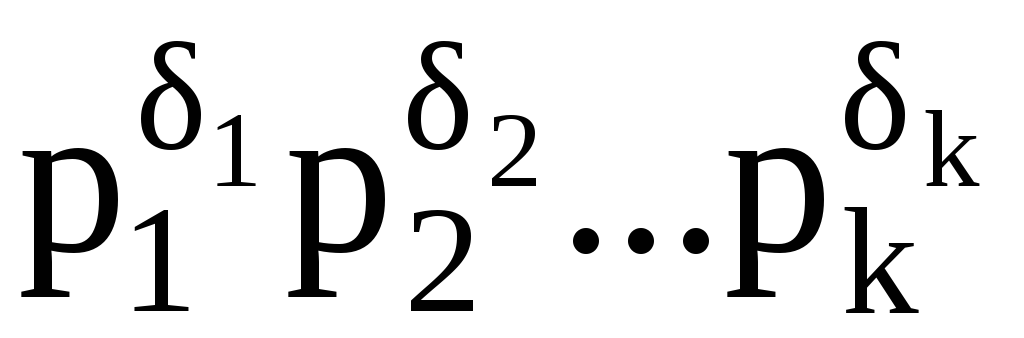 ,
,
где
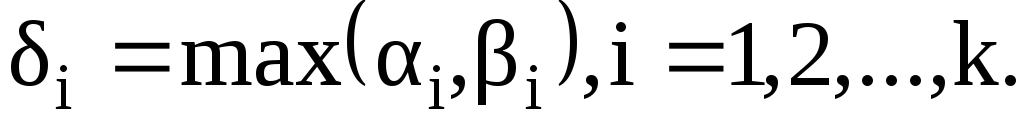
Множество простых чисел
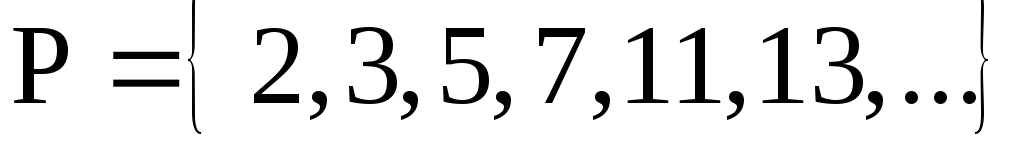 .
.
Пример. Определить порядок перестановки  вида
вида
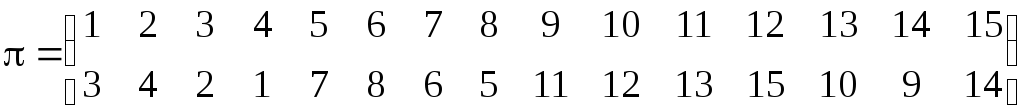 .
.
Решение. Представим перестановку в виде произведения независимых циклов, т.е.
.
Длины независимых циклов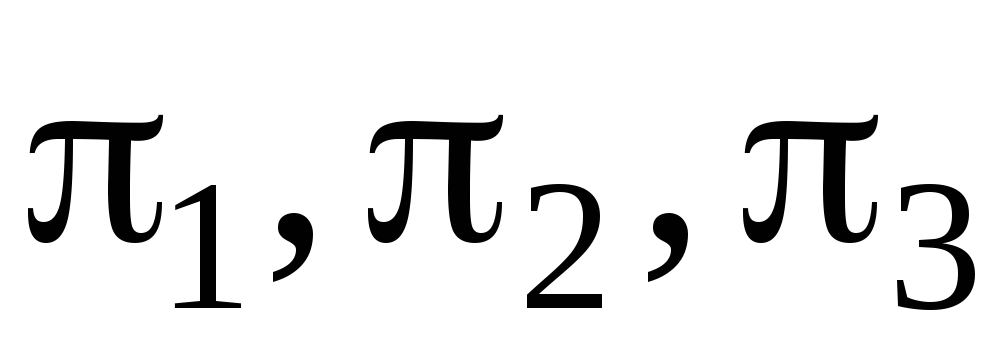 равны
равны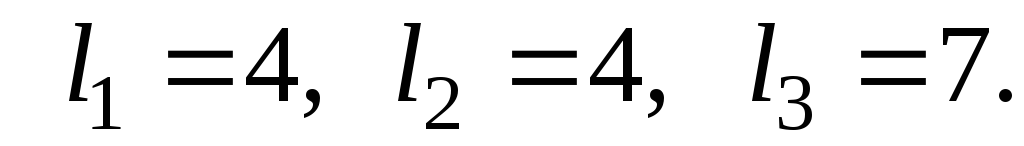
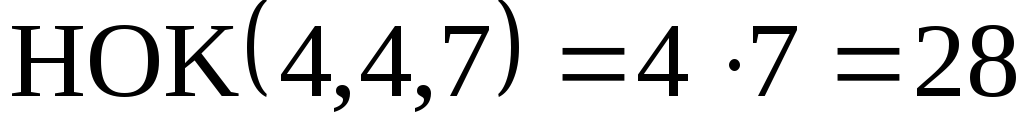
Следовательно, порядок рассматриваемой перестановки  равен 28.
равен 28.
Определение. Цикл длиной два называется транспозицией. Любая транспозиция имеет вид 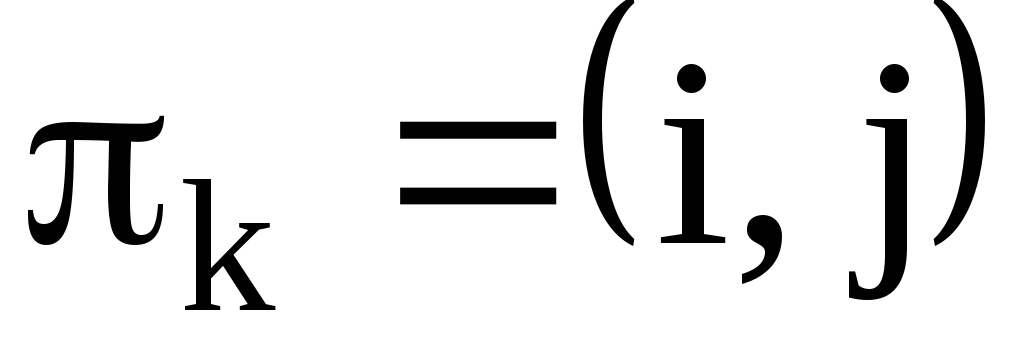 и оставляет на местах все символы за исключением
и оставляет на местах все символы за исключением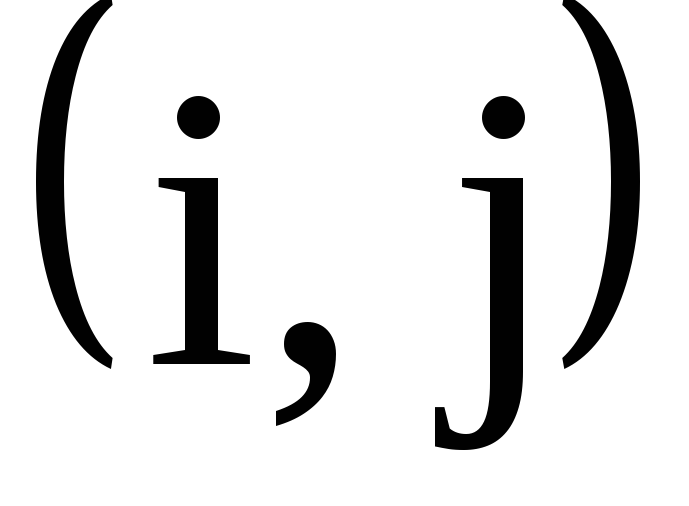 .
.
Теорема. Каждая перестановка  может быть представлена в виде произведения транспозиции.
может быть представлена в виде произведения транспозиции.
Доказательство. Теорема будет доказана, если мы сможем представить в виде произведений транспозиций каждый из циклов k, входящих в разложения перестановки: 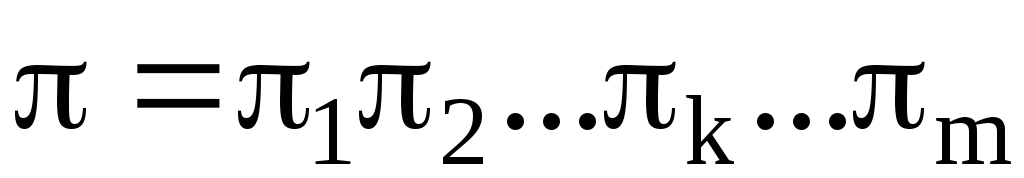 .
.
Рассмотрим произвольный цикл 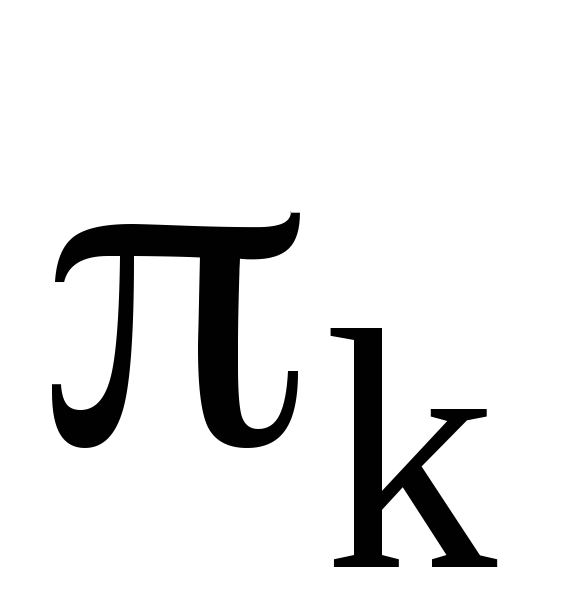 , например
, например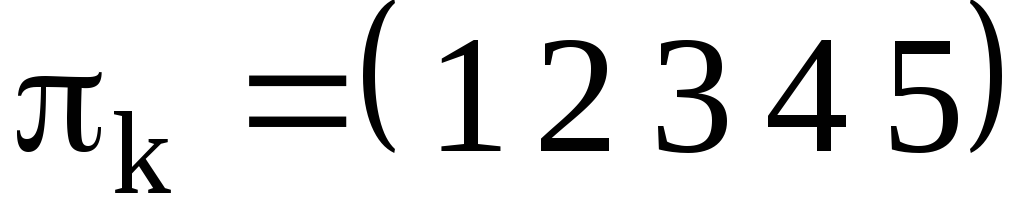 и произведем его разложение в произведение транспозиций.
и произведем его разложение в произведение транспозиций.
Алгоритм разложения цикла 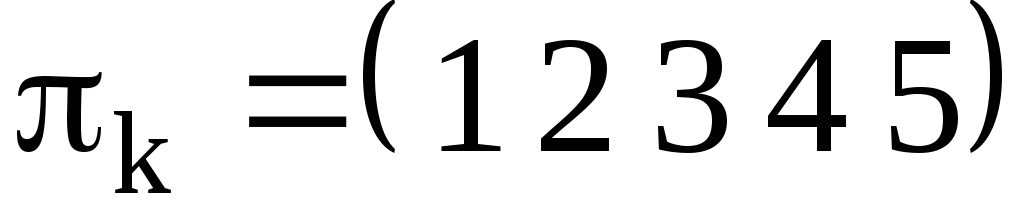 в произведение транспозиций представлен на рисунке 2.
в произведение транспозиций представлен на рисунке 2.
Цикл 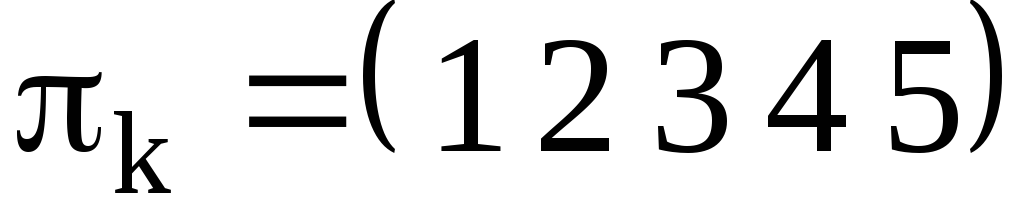 транспозиции
транспозиции
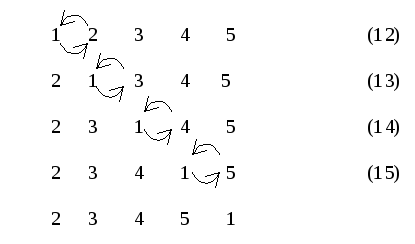
Рис 2. – Разложение цикла 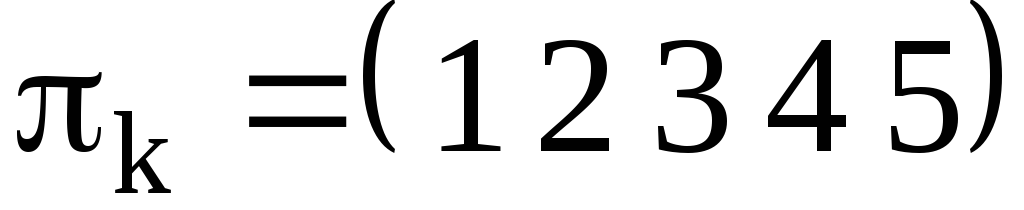 в произведение транспозиций.
в произведение транспозиций.
После завершения всех операций на месте каждого элемента цикла 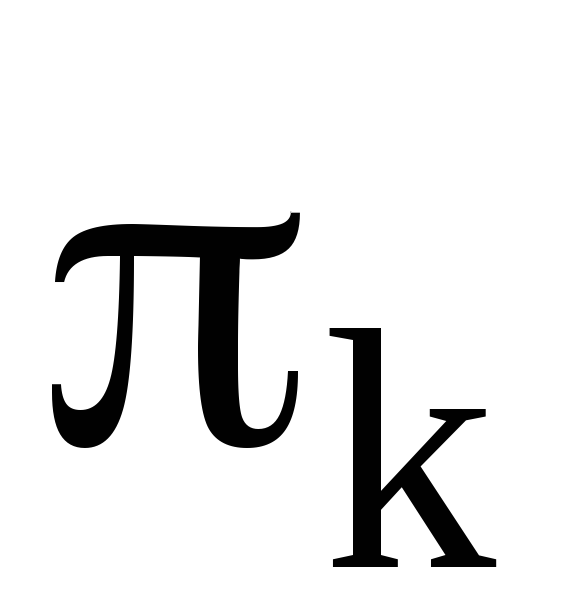 оказался следующий за ним элемент, а первый элемент перешел на последнее место. Таким образом, цикл
оказался следующий за ним элемент, а первый элемент перешел на последнее место. Таким образом, цикл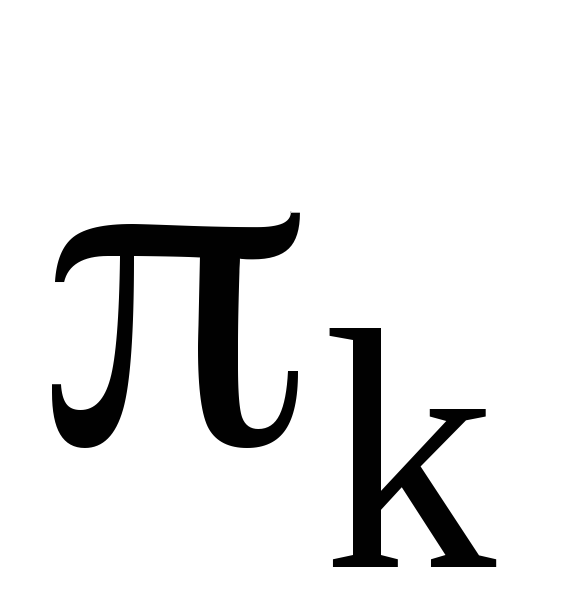 оказался разложенным в произведение транспозиций:
оказался разложенным в произведение транспозиций:
Естественно, это разложение не единственно. Например
.
Важно другое – и в первом и во втором его разложении имеется равное количество транспозиций – четыре. Если 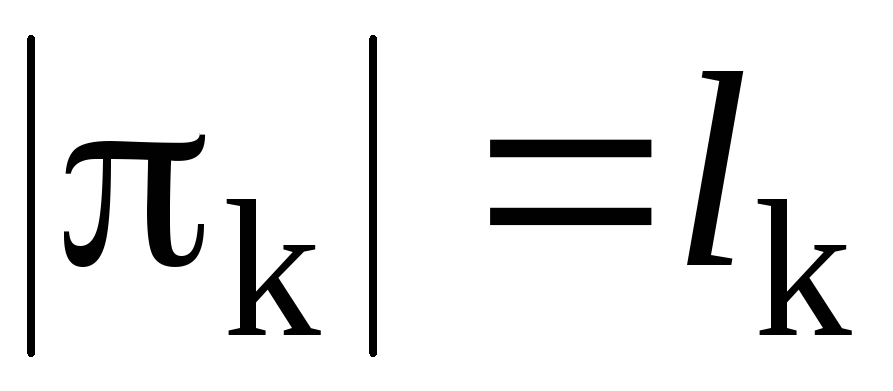 , то количество транспозиций равно
, то количество транспозиций равно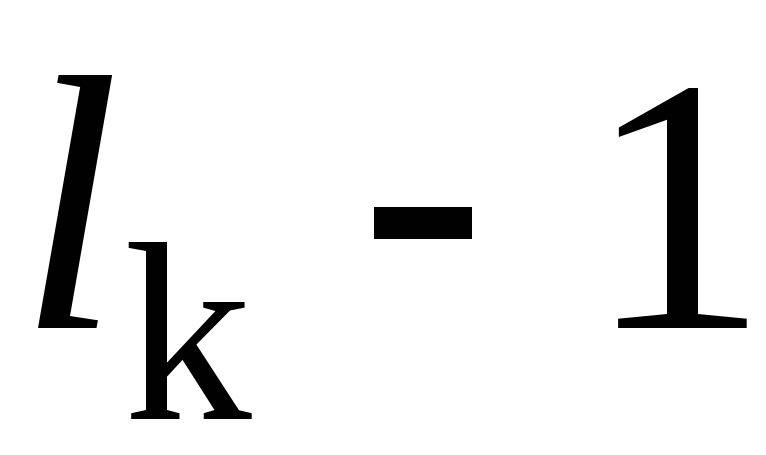 . Раскладывая аналогичным образом каждый цикл
. Раскладывая аналогичным образом каждый цикл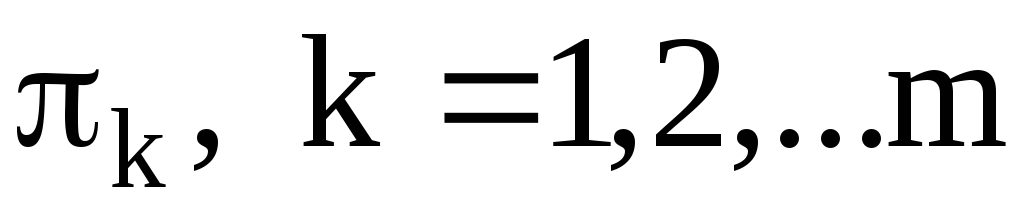 перестановки
перестановки в произведение транспозиции, мы получим разложение всей перестановки
в произведение транспозиции, мы получим разложение всей перестановки в произведение транспозиций.
в произведение транспозиций.
Замечание. Количество транспозиций в цикле 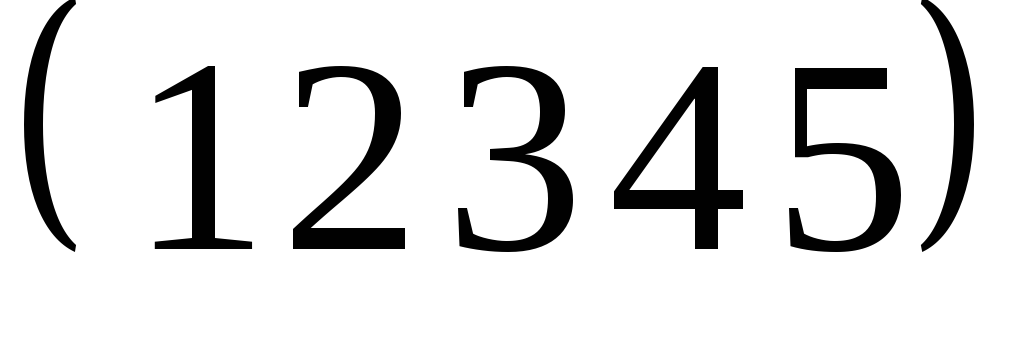 может быть и больше четырех! Возьмем произвольную транспозицию из разложения этого цикла, например,
может быть и больше четырех! Возьмем произвольную транспозицию из разложения этого цикла, например,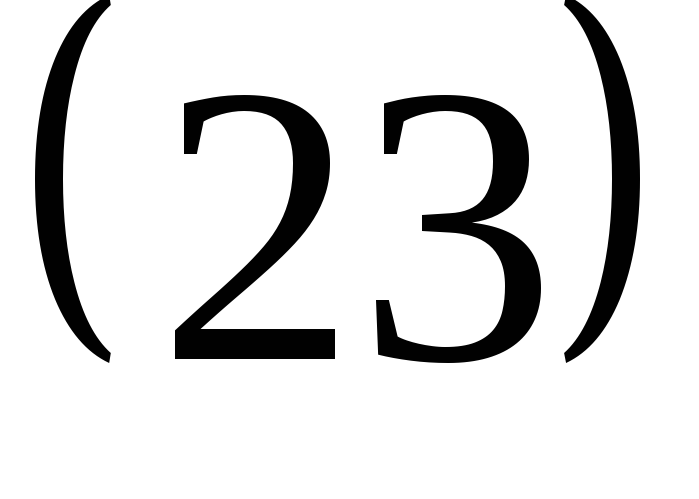 . Тогда произведение
. Тогда произведение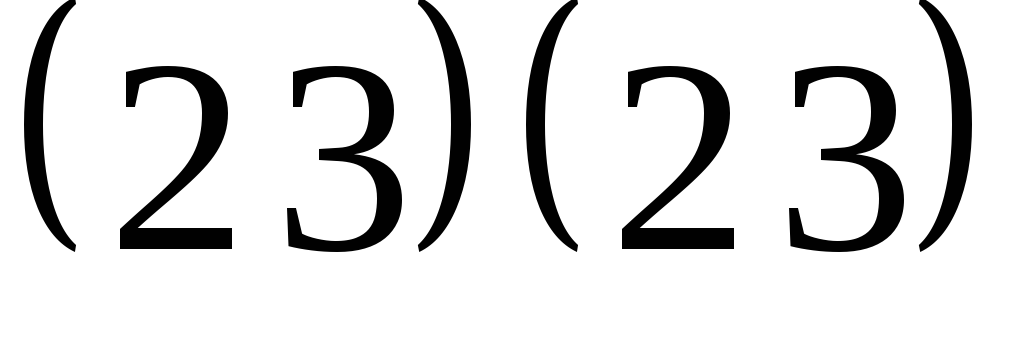 совпадает с тождественной перестановкой и цикл
совпадает с тождественной перестановкой и цикл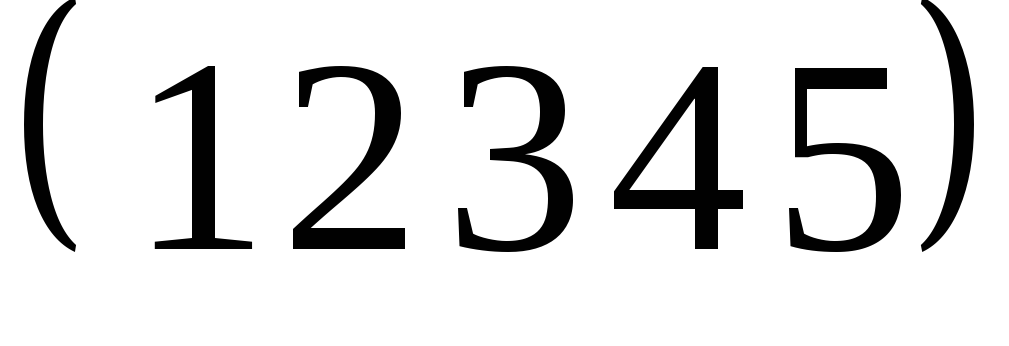 можно представить в виде
можно представить в виде
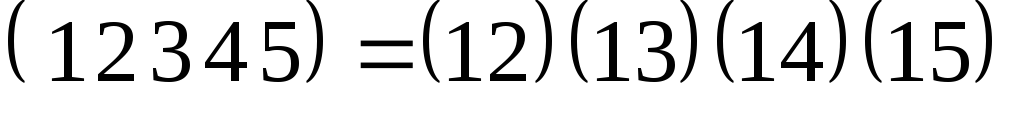
или
,
или
.
Легко заметить, что во всех этих случаях число транспозиций четно и равно 4,6,8. Ясно, что способ, «удлиняющий» разложение, не изменяет четности исходного разложения.
Теорема. Пусть – перестановка из 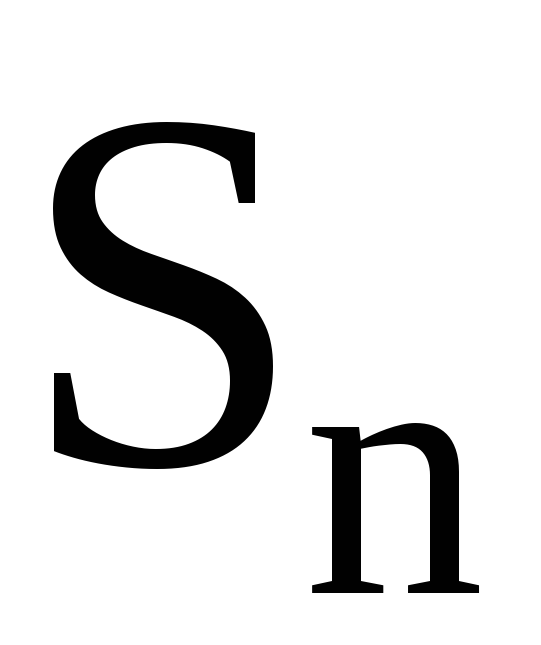 , а
, а
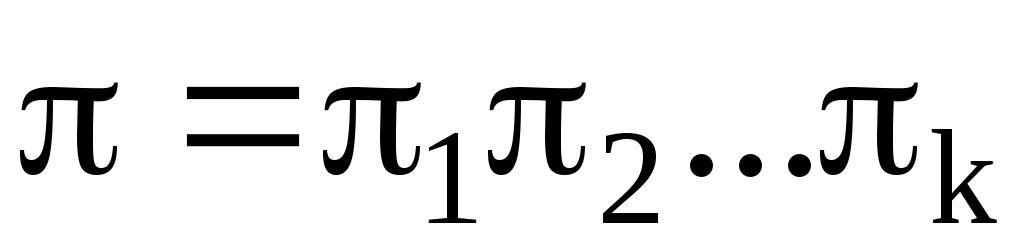 . (9)
. (9)
какое-либо разложение в произведении транспозиций. Тогда число
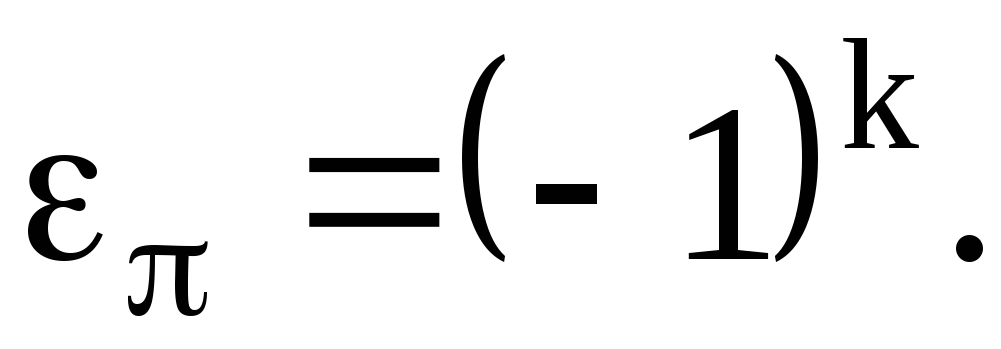 (10)
(10)
называется четностью (сигнатурой или знаком) перестановки и полностью определяется , т.е. не зависит от способа разложения перестановки в произведение транспозиций. Кроме того, если 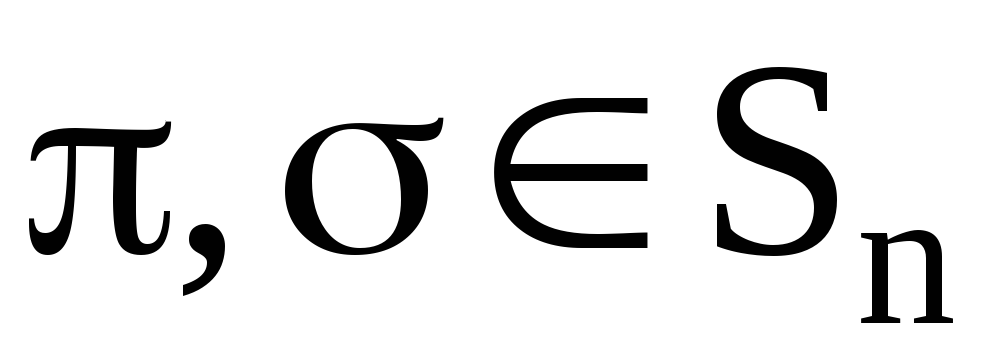 , то
, то
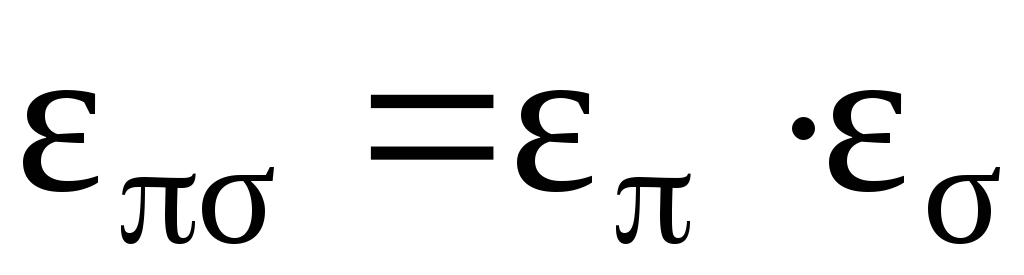 . (11)
. (11)
Данную теорему приводим без доказательства. Доказательство теоремы приведено в [1].
Определение. Перестановка  называется четной, если
называется четной, если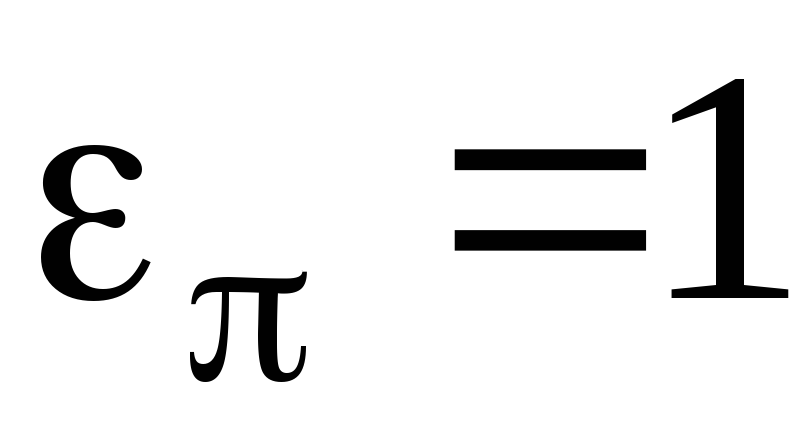 , и нечетной, если
, и нечетной, если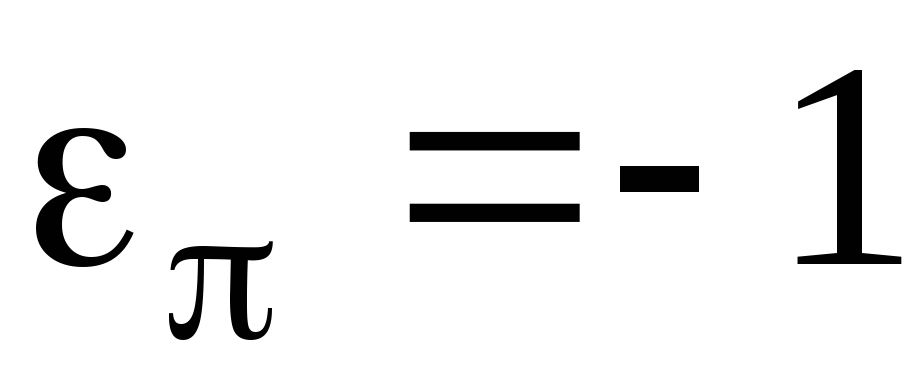 .
.
Из определения четности перестановки вытекает, что все транспозиции – нечетные перестановки. Действительно, если 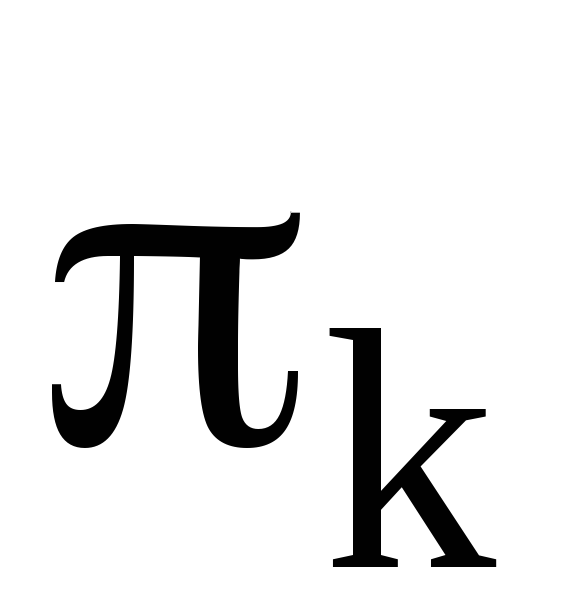 – транспозиция, то
– транспозиция, то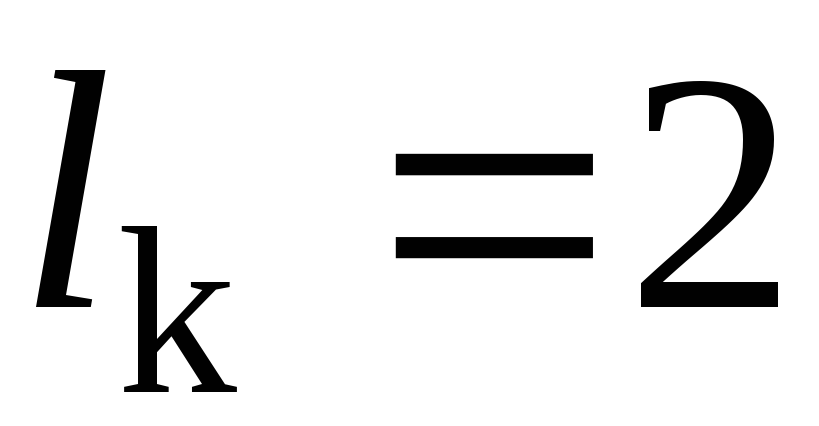 , тогда
, тогда
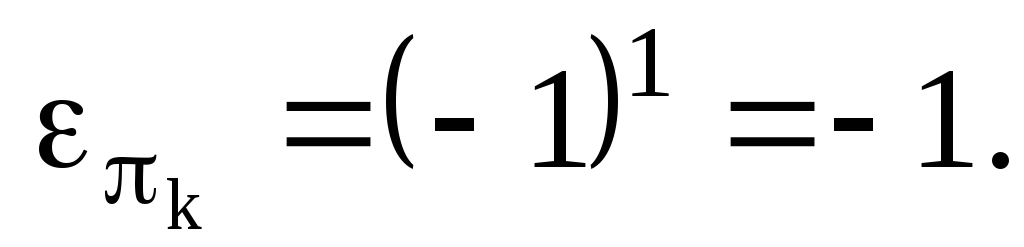
Следствие 1. Все четные перестановки степени n образуют подгруппу  порядка
порядка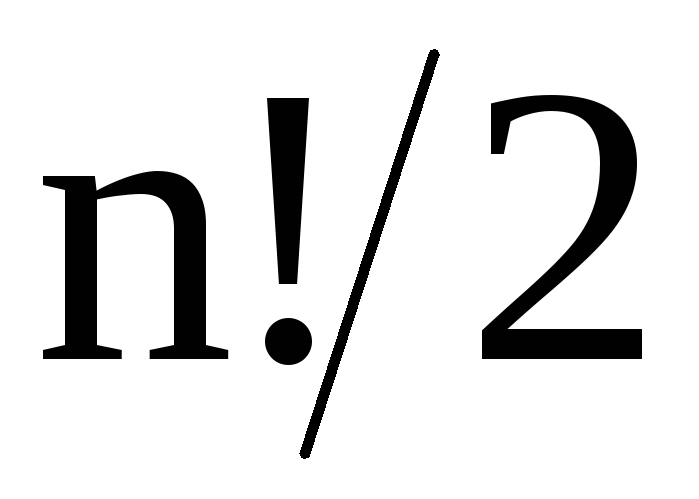 (она называется знакопеременной группой степени n).
(она называется знакопеременной группой степени n).
Следствие 2. Пусть перестановка  разложена в произведение независимых циклов
разложена в произведение независимых циклов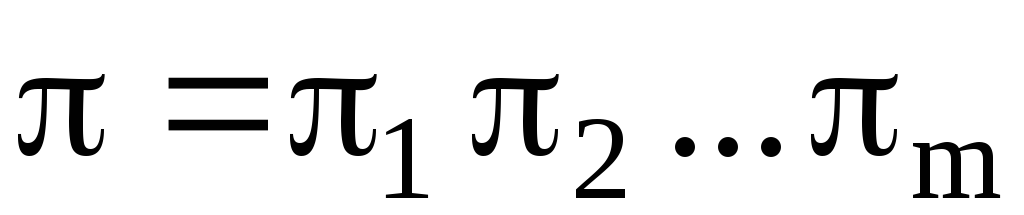 длин
длин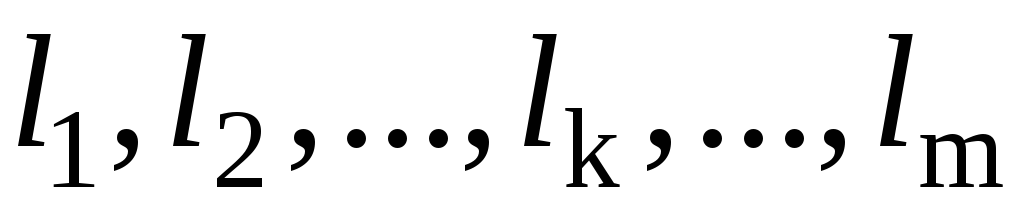 , где
, где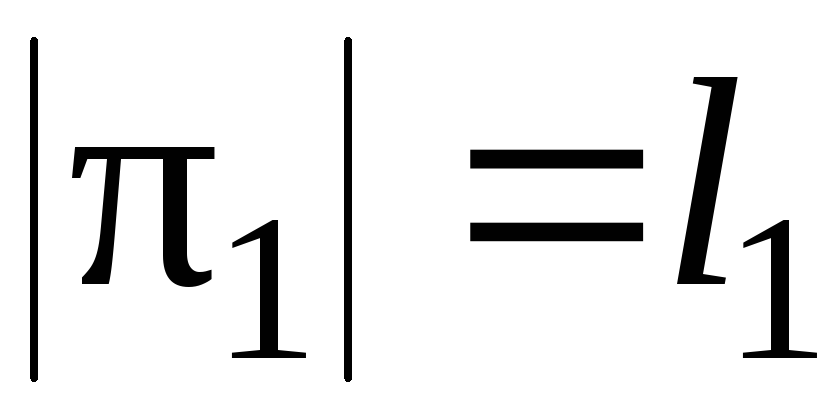 ,
,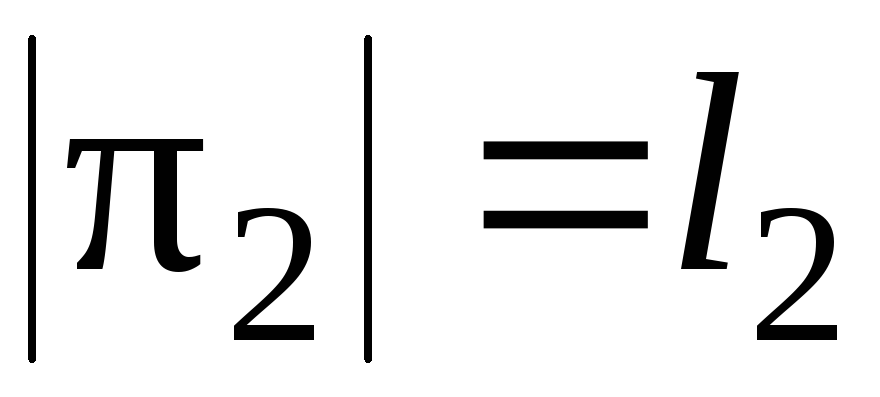 , …,
, …,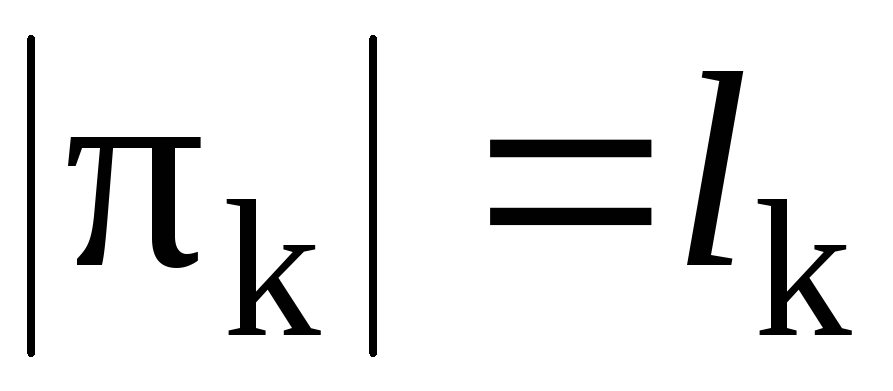 , …,
, …,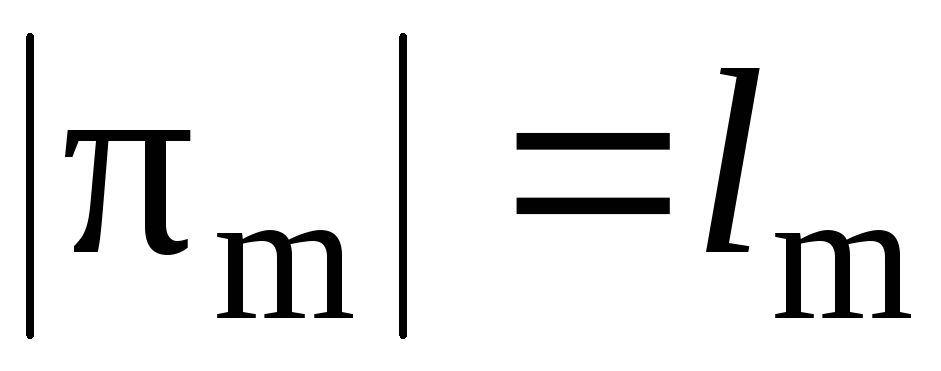 – длины независимых циклов.
– длины независимых циклов.
Тогда
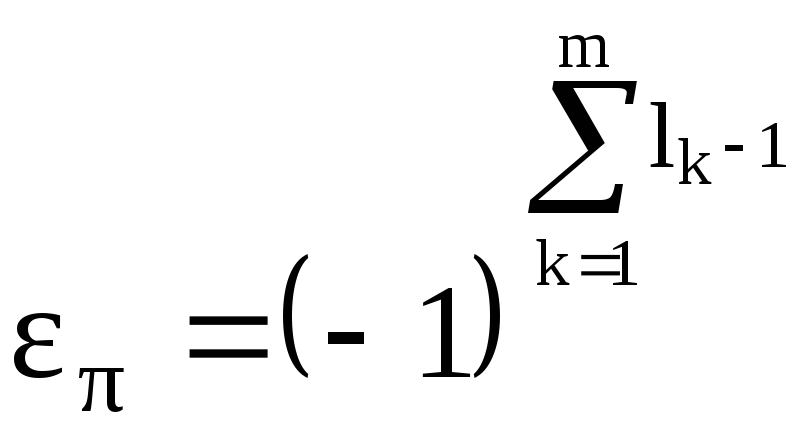 . (12)
. (12)
Доказательство. Действительно, по предыдущей теореме имеем
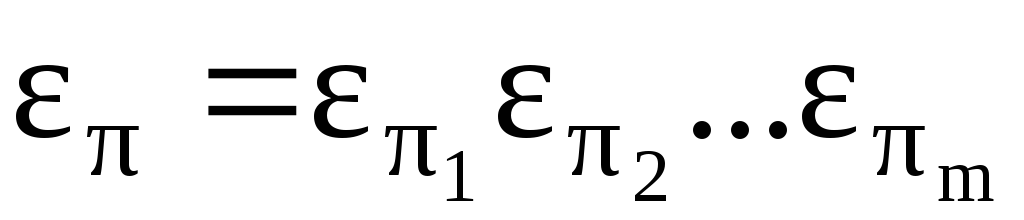 .
.
Кроме того, 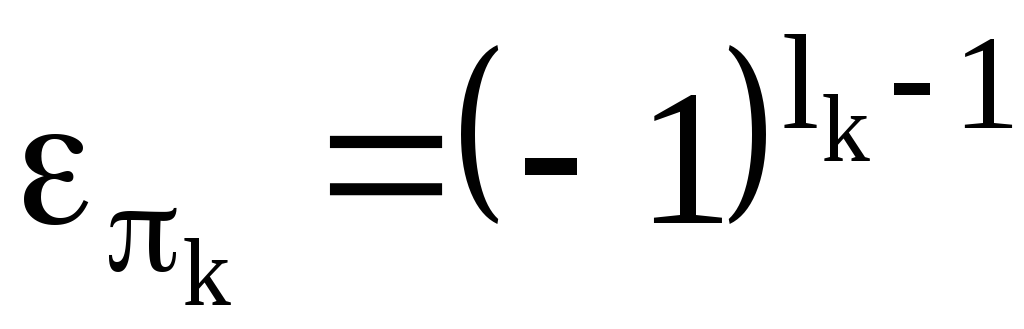 поскольку каждый
поскольку каждый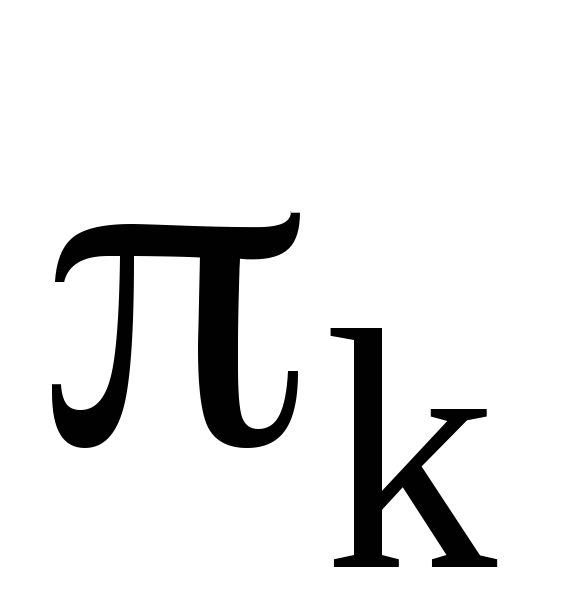 цикл записывается в виде произведения
цикл записывается в виде произведения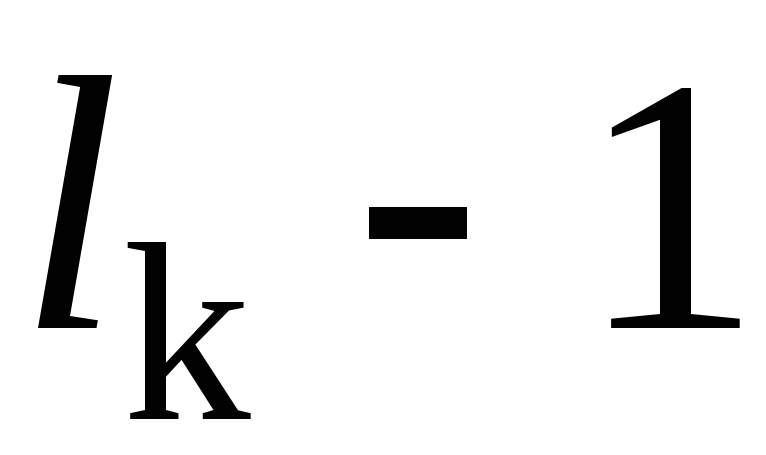 транспозиций, то
транспозиций, то
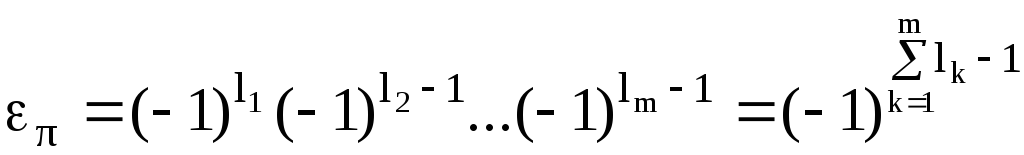 .
.
Соседние файлы в папке SAVE
- #
- #
- #
- #
Источник
Пусть – конечное множество из элементов. Поскольку природа его элементов для нас несущественна, удобно считать, что . Взаимно однозначное отображение называется перестановкой из элементов (длины ).
В развернутой и наглядной форме перестановку : , , изображают двухрядным символом
полностью указывая все образы:
.
Число различных перестановок из чисел равно произведению , обозначаемому .
Множество всех перестановок длины будем обозначать символом .
Перестановки перемножаются в соответствии с общим правилом композиции отображений: То есть под произведением перестановок будем понимать их суперпозицию.
Например, для перестановок
,
имеем
В то же время
так что
Умножение перестановок подчиняется следующим правилам.
1. Умножение ассоциативно, то есть для всех .
2. обладает единичным элементом : для всех
3. Для каждой перестановки существует обратная
Эти три свойства дают основание говорить о группе, называемой симметрической группой степени .
Разложим теперь перестановки в произведение более простых перестановок. Идею разложения поясним схематически на примере указанных выше перестановок
,
Перестановка , носит название цикла длины 4, а перестановка – произведение двух независимых (непересекающихся) циклов и длины 2.
Каждая перестановка в является произведением независимых циклов длины . Это разложение в произведение определено однозначно с точностью до порядка следования циклов.
Обратим внимание на циклы длины 2.
Цикл длины 2 называется транспозицией.
Любая транспозиция имеет вид и оставляет на месте все символы, отличные от
Говорят, что элементы и образуют относительно перестановки правильную пару, если
Если то элементы образуют неправильную пару, которая также называется инверсией.
Если количество инверсий в перестановке ( ) является числом четным (нечетным), то перестановка называется четной (нечетной).
Знаком перестановки ( ) называется функция, определяемая следующим образом:
Утверждение. Пусть перестановка разложена в произведение независимых циклов длин Тогда .
Свойства перестановок.
1. Произведение четных перестановок – четная перестановка.
2. Произведение четной перестановки на нечетную – есть нечетная перестановка.
3. Умножение на транспозицию меняет четность перестановки.
4. Четные перестановки образуют группу.
5. Перестановка и ей обратная имеют одинаковую четность.
6. Число четных и нечетных перестановок равно
2. Элементы теории колец (кольцо многочленов)
Понятие кольца и поля. Свойства
Кольцо – непустое множество с определенными на нем двумя бинарными операциями «+» и « », условно называющимися сложением и умножением, удовлетворяющее следующим свойствам:
1) – является коммутативной (абелевой) группой;
2) выполняется ассоциативный закон
3) справедливы следующие равенства , .
Если относительно умножения выполняется закон коммутативности, то кольцо коммутативно.
Если в существует нейтральный элемент 1 относительно умножения, то кольцо называется кольцом с единицей (1 – единичный элемент).
Элементы, у которых есть обратный элемент относительно умножения, называются единицами кольца (обратимыми элементами).
Множество единиц кольца образует группу
множество элементов кольца, рассматриваемого относительно сложения, называется аддитивной группой кольца.
Ненулевые элементы называются левым и правым соответственно делителями нуля, если . Оказывается удобным и сам нуль считать делителем нуля.
Если в кольце нет делителей нуля, отличных от самого нуля, то есть если из следует, что или , или , то говорят о кольце без делителей нуля. Если, кроме того, кольцо коммутативно, то оно называется целостным.
Коммутативное кольцо с единицей, в котором любой ненулевой элемент имеет обратный, называется полем.
Область целостности – коммутативное кольцо с единицей, в которых нет делителей нуля.
Источник
ПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.
ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
Подробнее
0.5 setgray0 0.5 setgray1
05 setgray0 05 setgray Лекция 4 ОПРЕДЕЛИТЕЛИ Определители порядка > Пусть A K a a a a 2 a 2 2 a 2 A = a a2 a a a a 2 A =, A a 2 2 2 = a a2 = A,A 2,,A,,, A = a a 2 ṇ a Определение Определителем, или детерминантом
Подробнее
0.5 setgray0 0.5 setgray1
0.5 setgray0 0.5 setgray1 1 Лекция 1 ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ УРАВНЕНИЙ 0. План лекции 1. Определитель второго порядка. 1.1 Система двух уравнений. 1.2. Метод исключения переменных. 1.3. Матрица 2 2. 1.4.
Подробнее
Конспект лекции 7 ОПРЕДЕЛИТЕЛИ I
Конспект лекции 7 ОПРЕДЕЛИТЕЛИ I План лекции Лекция Определители Определители второго порядка Система линейных уравнений; 2 Определение определителя второго порядка; 3 Запись через определители; 4 Свойства
Подробнее
Решения задач первой олимпиады
Решения задач первой олимпиады Задача 2006 1 Элементов какого порядка в группе S n больше: четного или нечетного? (Предложил А. Э. Гутерман.) Решение. При n = 2, 3 легко убедиться, что подстановок четного
Подробнее
Лекция 2. ?? сентября 2008
Лекция Квадратичные вычеты и невычеты Лектор: НЮ Золотых Записал: Е Замараева?? сентября 00 Содержание Квадратичные вычеты и невычеты Символ Лежандра Свойства символа Лежандра Квадратичный закон взаимности
Подробнее
Математические заметки
Математические заметки Том 0 выпуск 0 июнь 1966 УДК 512.643+512.552.2 Автоморфизмы полугруппы неотрицательных обратимых матриц порядка два над частично упорядоченными коммутативными кольцами Е. И. Бунина
Подробнее
Глава 1. Начала линейной алгебры
Глава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные
Подробнее
0.5 setgray0 0.5 setgray1
0.5 setgray0 0.5 setgray1 1 Лекция 6 СКАЛЯРНОЕ, ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 1. Скалярное произведение Определение 1. Углом ϕ между векторами a и b называется тот из углов, образованный
Подробнее
Математика 8 класс Многочлены
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными
Подробнее
Делимость целых чисел в задачах
Югорский физико-математический лицей В.П. Чуваков Делимость целых чисел в задачах Сборник задач Ханты-Мансийск 05 Делимость целых чисел в задачах: Сборник задач, – Ханты-Мансийск, Югорский физико-математический
Подробнее
ЛИНЕЙНАЯ АЛГЕБРА ВМЕСТЕ С MAPLE
ЛИНЕЙНАЯ АЛГЕБРА ВМЕСТЕ С MAPLE Усов ВВ Введение Представляю Вашему вниманию лекционный курс основ линейной алгебры, который впервые был прочитан в 2004 году на бизнес факультете НГТУ для специальности
Подробнее
1 Показатели. Первообразные корни.
1 Показатели. Первообразные корни. 1.1 Понятие показателя. Простейшие свойства. Определение. Будем говорить, что число a, (a, n) = 1 принадлежит показателю N по модулю n, если – минимальное число, такое
Подробнее
Нормальные подгруппы
Нормальные подгруппы Рассмотрим теперь следующий важный класс подгрупп ОПРЕДЕЛЕНИЕ Подгруппа H группы G называется нормальной, если для любого x G имет место равенство xh Hx Подчеркнем, что если H является
Подробнее
Делимость целых чисел
Делимость целых чисел Число а делится на число b (или b делит а) если существует такое число с, что а=bc При этом число c называется частным от деления а на b Обозначения: a – а делится на b или ba b делит
Подробнее
Глава 3. Определители
Глава Определители Перестановки Q Рассмотрим множество первых натуральных чисел которое обозначим как Определение Перестановкой P множества элементов из Q назовем любое расположение этих элементов в некотором
Подробнее
Лекция 1 МАТРИЦЫ. 1. Матрицы
Лекция 1 МАТРИЦЫ 1 Матрицы На этой лекции мы введём основное для всего курса аналитической геометрии понятие матрицы Необходимость введения понятия матрицы обусловлена, например, компактностью записи линейных
Подробнее
Занятие 7. Лемма 1. Для любых чисел a, b, q. 1. если a 0 или b 0, то существует d, т. ч. d = (a, b), причем (a, b) > 0;
Занятие 7 Число d называется наибольшим общим делителем (НОД) чисел a и b, если (1) d a и d b, а также (2) для всех x из x a и x b следует x d. В этом случае пишем d = (a, b). Лемма 1. Для любых чисел
Подробнее
Задача 11. Деление с остатком
XVIII Республиканский Турнир Юных Математиков Задача 11. Деление с остатком Лицей БГУ – 1 Автор: Пчелинцев Илья Научный руководитель: Шабан Светлана Аннотация Полностью решены пункты 1-3, 5 исходной постановки
Подробнее
Тема 1-7: Определители
Тема 1-7: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1 семестр) Перестановки
Подробнее
Коллоквиум по аналитической геометрии
Коллоквиум по аналитической геометрии Решения 07/11/2013 Напоминание некоторых обозначений. f : A B: f функция с областью определения A и областью значений B. Z, Q, R множества целых, рациональных, и действительных
Подробнее
Задачи ЕГЭ типа С6 с ответами и решениями
Сайт автора Его блог Рассылка I. Задачи Задачи ЕГЭ типа С6 с ответами и решениями I.1. Решите уравнение 3 m + 4 n = 5 k в натуральных числах. [Ответ] [Решение] I.2. При каких значениях х оба числа и целые?
Подробнее
ГЛАВА 6. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
66 ГЛАВА 6 ЛИНЕЙНЫЕ ПРОСТРАНСТВА Определение линейного пространства В гл 5 n-мерное векторное пространство было определено как упорядоченная система n чисел Для n-мерных векторов были введены операции
Подробнее
Лекция 10: Умножение матриц
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Вступительные замечания В данной лекции вводится операция умножения матриц, изучаются
Подробнее
Тема 1-13: Скалярное произведение векторов
Тема 1-13: Скалярное произведение векторов А. Я. Овсянников Уральский федеральный университет Институт естественных наук и математики Департамент математики, механики и компьютерных наук Алгебра и геометрия
Подробнее
Федеральное агентство по образованию Уральский государственный экономический университет Ю. Б. Мельников Основы теории групп Раздел электронного учебника для сопровождения лекции Изд. 2-е, испр. и доп.
Подробнее
Лекция 4: Векторное произведение векторов
Лекция 4: Векторное произведение векторов Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Вступительные замечания В этой и следующей
Подробнее
Занятие 6. a = bq + r и 0 r < b.
Занятие 6 Если не оговорено противное, в этой теме слово «число» означает целое число. Целое число a делится на целое число b, если существует целое число k, т. ч. a = bk. Также в этом случае говорят,
Подробнее
ПРИМЕНЕНИЕ ТЕОРЕМ СИЛОВА
ЛЕКЦИЯ 9 ПРОСТОТА ГРУППЫ A n ТЕОРЕМЫ СИЛОВА ПРИМЕНЕНИЕ ТЕОРЕМ СИЛОВА 1 ПРОСТОТА ГРУППЫ A n Мы доказываем теорему о том, что при n 5 группа A n является простой. Напомним ключевые леммы предыдущей лекции.
Подробнее
standard input standard output
Задача A. Арифметика Сначала найдём разность между заданными числами. Очевидно, что количество нечётных чисел будет не менее, чем [( a b + 1)/2] (между a и b a b + 1 число, из них не менее [( a b + 1)/2]
Подробнее
Лекция 11: Раскраска графа
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Происхождение понятия раскраски графа В приложениях теории графов нередко возникают задачи,
Подробнее
Тема 1-2: Элементы комбинаторики
Тема 1-2: Элементы комбинаторики А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1
Подробнее
Источник