Один моль одноатомного идеального газа проведен через обратимый цикл
Распознанный текст из DJVU-файла, 3 – страница
а) Объясните, па какой основе можно построитьграфик прямолинейной зависимости, при помощи которого можно определить состав (мол.%) смеси гелия и кислорода, отсчитывая плотность (г л-‘) при температуре 25’С н общем давлении ! атм (газы ведут себя, как идеальные). б) Постройте ~рафик и используйте его для определения состава смеси гелия и кислорода, плотность которой при определенных условиях равна 0,82 г л-‘.
Три компоненты скорости молекулы газа: о„, па и о,. Скорость о =(о’„-)- о’+ о’;)”. а) Напишите выражение для и„’, среднего четвертой степени скорости. (Этот и последующие ответы можно оставить в виде неопределенных интегралов. Тем не менее опи должны содержагь только массу каждой молекулы т, температуру Т, универсальные посзоянные и переменные интегрирования.) б) Напишите аналогичное выражение для о4. в) Если имеется различие между полученными иыражениями, помимо замены о иа о„, объясните, как о~о возникло. График представляет изотерму для 1 моля газа, который подчиняется уравнению состояния Р(г — Ь) = =агТ, где Ь ) О.
Объясните физический смысл наклона прямой и точки пересечения его с осью Р)’, Гарм !9 !8 Глава 1 1-3-9, 1-3-!О. (Р+ —,) (7 — аЬ) =айТ. 1-3-11. 1-3-12. 1-3-13. будут иметь вид 1-3-14. йг Р= = — А7~, 7 — в Обсудите справедливость этого уравнения состояния для реального газа при низких давлениях. Для некоторого гипотетического газа коэффициент термического расширения определяется так: а= у(ат) =й'(с )Т! ! г)- а коэффициент изотермического сжатия— Какому уравнению состояния подчиняется этот газу (Примите, что Сж Ср, й~ и йз — постоянные.) Покажите, что для газа Ван-дер-Ваальса Т„р= 8а)27Ьй 7~» Злй и Рвр а)27Р~ где Твр критическая температура, 7,» — критический объем и Р„» — критическое давление. Уравнение Ван-дерВаальса имеет вид Газ подчиняется уравнению состояния (Р+ аР’) Х Х(7 — Ь) =йТ, где а и Ь вЂ” постоянные.
Установите, имеет ли этот газ критическую точку. Если имеет, напишите уравнение состояния в приведенном виде. Для газа, описываемого уравнением Бертло. Р = йТУ7 — Ь) — а(ТР, выразите а, Ь и й через критические постоянные и напишите уравнение состояния в приведенных переменных. Покажите, что кРитические постоанпые Т„р, Рвр и Рвр для газа, который имеет уравнение. состояния Р— в-Атг лУ У вЂ” в Т„,=(4~~), 7„,=2Ь и Р’р ь (аьр~ Предложено следующее уравнение состояния для не- идеального газа: где à — мольный объем, А, ‘В и т — характеристиче.
ские постоянные газа. Если это уравнение может быть применено к реальному газу, то оно должно предсказать: !) приближение к идеальному газу при давлении, равном нулю, или прн бесконечном объеме, т.е. Р77йТ-+ ! прн Г- оо; 2) существование критической точки при положительных Гвр, Т, р и Рв . Желательно установить, каким условиям должпй удовлетворять постоянные А, В н т для того, чтобы уравнение отвечало этим двум предсказаниям.
а) Выразите РГ7ЙТ через А, В, т, й, Т и 7. 6) Если Л и ВФО, то какие требования необходимы, чтобы Р7(йТ- ! при 7- ооу в) Выразите (дР/д7)г и (д’Р~дЧв)г через А, В, т, й, Т и 7. г) Выразите критический объем 7вр через А, В, т и й. д) Какие условия должны быть наложены на А, В или т, чтобы Гвр было положительпымр с) Выразите критическую зеыпературу Т„р через А, В, т и й. ж) Какие условия должны быть наложены на А, В или т, чтобы Твр была положительна? э) ‘Обсудите физический смысл условий, которым должны удовлетворять А, В и т.
21 Глава II ПЕРВЫО ЗАКОН ТЕРМОДИНАМИКИ И ТЕРМОХИМИЯ 11-1-5. Таблица О.г Стандартные знтальнни обРазованна АН1 тоз (ккал смоль ‘) соецннсинй и нх теплоемкости Ср =а+ ЬТ+ сТ + бТз+ /Т (кал ° еК ° моль ~) ! 1-1-6. ьи Соедввенне ! тзз’ ккал мочь 4,03 1,14 0 0 6,79 0,98 0 0 10,57 2,10 О 0 7,219 2,374 2,67 0 — 2,04 — 0,11 — 2,06 0 298 — 2000 298 — 2000 298 — 2000 298 — 1500 !г,г 6,955 3,675 7,40 0 6,148 3,102 — 9,23 0 6,796 ! 1,588 — 3,0 ! 5 2,057 298- ! 500 298 — 1500 298 — 1500 299 т, к БББ Приведенные данные неволь»тюте» в задачах втой главы. Р, атн т,’к Точка РАЗДЕЛ 1РП 24,4 24,4 12,2 Покажите, что для процесса нагревания идеальнога газа 298 596 298 И-1-1.
Характер процесса Стали» о, кал ю, кзл Ь У, «ал Ьи, кал Используя уравнение (д(//дУ)г = Т (дР/дТ) р — Р, покажите, что (д(//д)з)т = О для газа, которыи подчиняется уравнению состояния РГ = ВТ, Выведите математическое выражение, включающее только постоянные и легка измеримые физические параметры, для работы тр, совершаемой газом в окружающеи среде. Газ подчиняется уравнецизо состояиа ния Р)х= пКТ вЂ” — и расширяется обратимо ог У объема )т! да объема кт при постоянной температуре. Найдите для ! моля газа, уравнение состояния кото- рога Р)7=ОТ+ АРТ вЂ” ВР, работу обратимого изотермического расширения от объема Гх! до объема Рт.
11-1-2. Изохорн- ческий Изобари- ческнй Изотермн- ческий 1 — ь г г — 3 3 — »1 11-1-3. Полный цикл !1-1-4. 11-1-7. С (графит) СО (г) СОз (г) НзО (т) Н,О (м) Н,Я (г) ЫНз (г) О, (г) ЗОз (т) 0 — 26,4157 — 94,0518 -57,7979 — 68,3174 — 4,815 — ! 1,04 0 -70,96 3 з -з И»терзал л а ~О е !О и ~аз ! 1О ‘ тенвераттр, к Перона закон термодинамики и термолимил 1’ — мольный объем, а А и  — характеристические постоянные газа. Клапан цилиндра, содержавшего !О л газа при давлении 25 атм и температуре 25’С, открыт в атмосферу, давление в которой 760 мм рт. ст., а температура 25’С. Считая этот процесс изотермическим, определите работу (л-агм) процесса расширения газа.
Один моль одцоатомпого идеального газа проведен через обратимый цикл, показанный на рисунке. Заполните пустые места в таблицах, приведенных ниже. Один моль одноатомного идеального газа проведен через обратимый цикл, показанный на рисунке, За- Глава П Точка Р, атм р. л т, к 298 595 595 4 Е ма,з Характер процесса Сталкк Изобари- ческий Изотермп- ческий Изохори- ческий ! — т 2 г — 3 3 — р ! гг,4 к,л т, ‘к Полный цикл 1 1 0,5 24,4 48,8 48,8 Вычислите конечную температуру обратимого адиабатического расширения 100 г аргона от 1О до 50 л; начальная температура 25’ С. Вычислите максимальную работу а) изотермического и б) адиабатического расширения 2 молей азота от !О до 20 л (считая его идеальным газом) с начальной температурой 25’С.
Примите, что Ст — — з/з/1. Исходя из уравнения 1лзт=( — 1/СР) (дН/дР)т, выведите формулу Коэффициент Джоуля — Томсона для кислорода равен +0,366’С атм ‘. Приняв, что этот коэффициент не зависит от температуры, определите конечную температуру газа, когда !О молей кислорода с исходным давлением 20 атм и температурой 20’С расширяются, как в опыте Джоуля — Томсона, сквозь пористую мембрану до конечного давления 1 атм. При определении энтальпии сгорания нафталина (С»еНз) в кислороде в калориметрической бомбе найдено (8], что при сгорании 1,1226 г нафталина температура калориметрической системы возросла на 4,0630’С.
Средняя температура опыта равна 18’С. Повышение температуры исправлено с учетом энтальпин сгорания запальной проволочки и образования сажи, окиси углерода и азотной кислоты. Теплоемкость калориметрнческой системы 2660 кал; молеку- 11-1-9. Характер процесса Сталка 1 1-1- ! О. Изобари- ческий Изохори- ческий Изотерми- ческий ! — г 2 — р 3 3 — р ! П-1-! !. Полный цикл П-1-12. 11-1-13 и Е и гвв г,к полните пустые места в таблицах, приведенных ниже.
Точка Р, атм 1». л е, кал и, кал ЬУ, кал ЬН, «ал Один моль одноатомного идеального газа проведен через обратимый цикл, показанный на рисунке. Заполните пустые места в таблицах, приведенных ниже. Первый закал термодинамики и термохимия Е, кал и, кал ЕУ, кал ЛН, кал терлгодинамики и термокимил Глава П Первый закон 24 11-1-!4. 11-1-20. 1Н-15. 1Н-16, 1Н-21. Эитеиьиии рестиореиии. «кол иоле Соедииеиие ЗСаО В,Оз 2СаО В,Оз СаО ВзОз СаО 2взОз СаО В,О, ЬПз = -82,423 ЬП, = -50,287 ЬПз = — 20.259 ЬП, = — (0,080 Ь77, = -45,380 ЬН, = — 32,85 И-1-22.
!1-1-17. 11-1-18. ЛНяя= — 94,052 ккал ‘зЧС (тв) + ~/зОз (г)— -р%0з(тв) + СО,(г) ЛНзез = — 285,80 ! Н-19. ЛНрзз = — 200, 16 % (тв) + /зОз(г) ->%Од(тв) Н-1-23. лярный вес нафталина 128,! ! г моль-‘. Определите энтальпию сгорания 1 моля нафталина прн 18’С. Калорическая ценнос~ь пищевых продуктов (факп(- чески энтальпия сгорания единицы массы пищевых продуктов) может быть определена измерением теплоты, выделяющейся при горении взвешенного образца пищи при условии постоянства объема в калориметрической бомбе. Выделяющееся тепло при полном сгорании 1 г (3 !О-з моля) куриного жира в этих условиях (постоянный объем) составляет 1О ккал при 37’ С. Определите калорическую ценность куриного жира (кал г() при 37’С и постоянном давлении, т.е.
стандартную теплоту сгорания куриного жира при 37’С. Реакция может быть представлена уравнением Сз,НззО, (тв) + 270з(г) — и 20СОз (г) + 16НзО (ж). Определите эптальпию плавления льда (кал моль ‘) при — 10’ С из следующих данных: Ср(НзО, тв) = = 9 кал ° моль ‘ ‘К ‘; Ср(НзО, ж) = 18 кал ° моль ‘ Х Х ‘К ‘, ЛЙ плавления льда при 0’С 1435 кал моль-‘. Ниже приведены энтальпин растворения некоторых соединений типа пСаО л(ВазОз в 1 н. НС! прн 298,16’ К [9): Вычислите ЛН для реакции ЗСаО + ВзОз = ЗСаО.
ВзОз. Для реакции 2Аз(тв)+ 5Вз(г) = 2АзВз(г) Л!гздз = = 15 000 кал. Определите ЛНздз для этой реакции. о Стандартная энтальпия сгорания ЛНздз твердого нафталина (С(д!1з) равна — 1231,6 акал ° моль ‘. Продукты сгорания — СОз и жидкая вода. Найдите стандартную энтальпию образования нафталина при 25’С. о а) Стандартная энтальпия сгорания (ЛН, ) кристаллической бензойной кислоты (СаНзСООН) при 25’С до СОз (г) и НзО (ж) равна — 771,72 ккал моль-(, Найдите ЛН’ и Л(7′ образования бензойной кислоты пз простых веществ при 25’С. б) Найдите стандарт- ную энтальнию образования ЛН’ кристаллической бепзойной( кислоты при 100′ С.
Примите, что в данном интервале температур теплоемкости приведенных веществ постоянны: сензсоон (крист( с (грзззит( нз(гз оз (г( Ср, кал ° ‘К-‘ моль-‘ 35,( 2,0 4,9 5,0 Оцепите Л77’ ионизации водных растворов л(-хлорфе- пола (м-ХФ) [!0) на основе следующих данных: о лыХФ(ж)- л(-ХФ(ац) ЛН(=-674 кал моль ‘ м-ХФ (ж) + ОН (ац) -о ЛНз 7540 кал мол НзО(ж)-оН'(ац)+ ОН (ац) ЛНз=!3,5 ккал моль ‘ При 298,16’ К стандартная энтальпия сгорания цис- гексагидроиндана (цис-СзНм) равна — 1351, 60 ккалХ Х моль-‘ [11). Процесс сгорания может быть представ- лен уравнением: цис-СдНы (ж)+ 13 Оз (г) — о 9СОз (г)+ 8НзО (ж). а) Вычислите стандартную энтальпию образования ! моля цис-гексагидроиндана из простых веществ при 298,16′ К б) Какой будет ответ, если за стандартное состояние углерода принят алмаз вместо графита? С(алмаз) — С(графит) ЛНздз= — 0,45 ккал. Оцените стандартную энтальпию образования карбида вольфрама %С (тв) на основе следующих данных [12): С(графит) + О,(г) — «СО,(г) Измерена [13) стандарп(ая эитальпия гидрирования циклогексена и бензола и получены следующие ре- Глава П зультаты: Ср кал К .моль Реакция ЛН’, ккал моль ‘ Соелииеяие 8,89 6,97 6,94 18,02 ХНа О, Хя НеО (ж) — 28„59 — 49,80 1 1-1-28.
ан обрааоааиия, ккал.моль е Ср, кал «К моль 8,00+ 0,002 Т 7,00 8,00 А В Аве П-! -24. П-1-29. П-1-20. — 19,5 — 17,5 — 44,0 П-1-26. П-1-27. П-1-30. н, Нэ от’ е [ ! Н 2 2 1ь2 Н, Н б) Н[ [ +ЗН, — и Н н, На основании реакции (а) определите стандартную энтальпию образования бензола н объясните, почему полученная величина не совпадает с измеренной ( — 49,80 ккал моль-‘).
Стандартная энтальпия сгорания борогидрнда алюми- ния А1(ВНе)в (ж) равна — 989,! икал моль ‘ при 298,2’ К [14). А! (ВН,), (ж) -1- 6 Ое (г)— -ь ‘/,А!,Ов (крист. корунд)+ в/еВвОв (крист) + + 6НеО (ж). Вычислите стандартную энтальпию образования А1(ВНе)б (г). Энтальпия испарения А1(ВН,), (ж) 7,2 ккал моль ‘, а энтальпии образования необходи- мых для расчета соединений равны: А1еОз(крист. корунд) — 399,09 ккал моль-‘, ВеОа (крист) — 303 ккал ° моль ‘.
Источник
30. Молекулярная физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол ((C_6H_6)) при температуре кипения (t =80^circ C). При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который при изобарном расширении совершает работу, поднимая поршень. Удельная теплота парообразования бензола ( L = 396cdot 10^3 )Дж/кг, а его молярная масса (M =78cdot 10^{-3}) – кг/моль. Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь. “Досрочная волна 2020 вариант 1”
По первому закону термодинамики [Q=Delta U+A,quad (1)] (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии, (A) – работа газа.
А количество теплоты, полученное системой равно [Q=Lm,quad (2)] где (m) – масса образовавшегося пара.
Так как процесс испарения прошел не до конца, то данный процесс изотермический, а значит работа газа будет совершаться за счет изменения массы пара [A=dfrac{m}{M}RT,quad (3)] где (T) – температура газа в Кельвинах.
Объединим (1), (2) и (3) и найдем отношение (dfrac{Delta U}{Q}) [dfrac{Delta U}{Q}=dfrac{Q-A}{Q}=1-dfrac{dfrac{m}{M}RT}{Lm}=dfrac{RT}{LM}=dfrac{8,31 text{ Дж/(К$cdot$моль)}cdot (273+80)text{ К}}{396cdot 10^3text{ Дж/кг}cdot 78cdot 10^{-3}text{ кг/моль}}approx 90,5 %]
Ответ: 90,5
Цикл тепловой машины, рабочим веществом которой является (nu) молей идеального одноатомного газа, состоит из изотермического расширения, изохорного охлаждения и адиабатического сжатия. Работа, совершённая газом в изотермическом процессе, равна (A), а КПД тепловой машины равен (eta). Максимальная температура в этом цикле равна (T_o). Определите минимальную температуру (T) в этом циклическом процессе.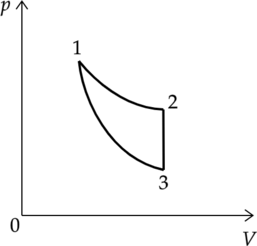
Процессы:
1-2 — изотермический
2-3 — изохорный
3-1 — адиабатический
КПД тепловой машины равен: [; ; ; ; eta = dfrac{A_text{ц}}{Q_text{н}} ; ; ; ; (1)] где (A_text{ц}) — работа, совершенная газом за цикл, (Q_text{н}) — количество теплоты, полученное газом от нагревателя.
Работа газа за цикл есть сумма работ газа в каждом процессе: [A_text{ц} = A_{1-2} + A_{2-3} + A_{3-1}] Так как в процессе 2-3 объем газа постоянен, то его работа равна нулю.
Тогда работа газа за цикл равна: [; ; ; ; A_text{ц} = A_{1-2} + A_{3-1} ; ; ; ; (2)] Далее необходимо найти количество теплоты (Q_text{н}), полученное газом от нагревателя.
Для этого запишем первое начало термодинамики для каждого процесса.
Процесс 1-2: [Q_{1-2} = A_{1-2} + Delta U_{1-2}] Так как процесс 1-2 изотермический, то изменение внутренней энергии газа (Delta U_{1-2}) равно нулю.
Объем газа увеличивается, следовательно, газ совершает положительную работу.
Отсюда получаем, что: [Q_{1-2} = A_{1-2} > 0 ; ; ; Rightarrow ; ; ; ; Q_{1-2} > 0] Процесс 2-3: [Q_{2-3} = A_{2-3} + Delta U_{2-3}] Так как процесс 2-3 изохорный, то работа газа (A_{2-3}) равна нулю.
Давление газа уменьшается, следовательно, его температура также уменьшается (для изохорного процесса (p sim T)).
Следовательно, изменение внутренней энергии газа отрицательно.
Отсюда получаем, что: [Q_{2-3} = Delta U_{2-3} < 0 ; ; ; Rightarrow ; ; ; ; Q_{2-3} < 0] Процесс 3-1:
Так как процесс 3-1 адиабатный, то (Q_{3-1} = 0): [; ; ; ; Q_{3-1} = A_{3-1} + Delta U_{3-1} ; ; ; Rightarrow ; ; ; ; A_{3-1} = – Delta U_{3-1} ; ; ; ; (3)] Таким образом, количество теплоты, полученное газом от нагревателя равно: [Q_text{н} = Q_{1-2}] [; ; ; ; Q_text{н} = A_{1-2} ; ; ; ; (4)] Подставим (2), (4) в (1): [eta = dfrac{A_{1-2} + A_{3-1}}{A_{1-2}}] [; ; ; ; eta = 1 + dfrac{A_{3-1}}{A_{1-2}} ; ; ; ; (5)] Подставим (3) в (5): [; ; ; ; eta = 1 – dfrac{Delta U_{3-1}}{A_{1-2}} ; ; ; ; (6)] Изменение внутренней энергии газа в процессе 3-1 равно: [; ; ; ; Delta U_{2-3} = dfrac{3}{2}nu R(T_1 – T_3) ; ; ; ; (7)] где (R) — универсальная газовая постоянная.
Подставим (7) в (6) и выразим искомую температуру: [eta = 1 – dfrac{dfrac{3}{2}nu R(T_1 – T_3)}{A_{1-2}}] [T_3 = T_1 – dfrac{2}{3nu R} (1 – eta)A_{1-2}] Температура (T_1) является максимальной в этом цикле, так как точка 1 на графике принадлежит изотерме 1-2, которая лежит выше, чем изотерма, проведенная через точку 3: (T_1 = T_o).
Следовательно, температура (T_3) является минимальной: (T_3 = T).
Работа (A_{1-2}) совершена газом в изотермическом процессе: (A_{1-2} = A).
Таким образом, искомая температура равна: [T = T_o – dfrac{2}{3nu R} (1 – eta)A]
Ответ: $T=T_o-dfrac{2}{3nu R}(1-eta)A$
В гладком вертикальном цилиндре под подвижным поршнем массой (M) и площадью (S) находится идеальный одноатомный газ. Поршень в равновесии располагается на высоте (h) над дном цилиндра. После сообщения газу количества теплоты (Q) поршень приподнялся, а газ нагрелся. Найдите, на какой высоте (H) над дном цилиндра находится поршень. Давление в окружающей цилиндр среде равно (p_o).
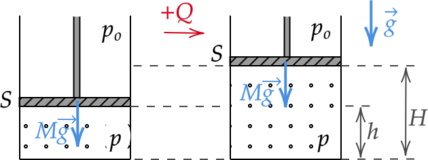
Рассматриваемый процесс — изобарный (так как поршень подвижный и количество вещества газа не изменяется).
Запишем первое начало термодинамики для изобарного процесса: [; ; ; ; Q = A+Delta U ; ; ; ; (1)] где (A) — работа газа, (Delta U) — изменение внутренней энергии газа.
Работа газа и изменение его внутренней энергии равны: [; ; ; ; A = pDelta V ; ; ; ; (2) ; ; ; ; ; ; ; ; ; ; ; Delta U = dfrac{i}{2}nu RDelta T ; ; ; ; (3)] где (p) — давление газа под поршнем, (Delta V) — изменение объема газа, (i) — число степеней свободы (для одноатомного газа (i = 3)), (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (Delta T) — изменение температуры газа.
Подставим (2), (3) в (1): [Q = pDelta V + dfrac{3}{2}nu RDelta T] Для изобарного процесса справедливо равенство: (pDelta V = nu RDelta T).
Тогда уравнение (4) примет вид: [; ; ; ; Q = pDelta V + dfrac{3}{2}pDelta V = dfrac{5}{2}pDelta V ; ; ; ; (5)] Давление внутри сосуда складывается из атмосферного давления и давления, оказываемого поршнем (так как у него есть масса): [; ; ; ; p = p_o + dfrac{Mg}{S} ; ; ; ; (6)] где (g) — ускорение свободного падения.
Изменение объема, занимаемого газом, после сообщения теплоты равно: [; ; ; ; Delta V = (H-h)S ; ; ; ; (7)] Подставим (6), (7) в (5) и выразим высоту, на которой будет находиться поршень над дном цилиндра: [Q = dfrac{5}{2}left( p_o + dfrac{Mg}{S} right) (H-h)S] [H=h+dfrac{2Q}{5(p_oS+Mg)}]
Ответ: $H=h+dfrac{2Q}{5(p_oS+Mg)}$
Два одинаковых теплоизолированных сосуда соединены короткой трубкой с краном. В первом сосуде находится (nu_1) =3 моль гелия при температуре (T_1 = 350) К, во втором (nu_2) = 2 моль аргона при температуре (T_2 = 400) К. Кран открывают. В установившемся равновесном состоянии давление в сосудах становится (p = 6 ) кПа. Определите объём (V ) одного сосуда. Объёмом трубки пренебречь. Ответ дайте в м(^3) и округлите до тысячных.
Так как сосуды теплоизолированные, а газ не совершает работы, то изменение внутренней энергии равно 0, то есть [U_1+U_2=U] где (U_1) – внутренняя энергия первого сосуда, (U_2) – внутренняя энергия второго сосуда, (U) – внутренняя энергия сосудов после открытия краника.
Или [dfrac{3}{2}nu_1R T_1+dfrac{3}{2}nu_2RT_2=dfrac{3}{2}left(nu_1+nu_2right)RT] Отсюда установившаяся температура [T=dfrac{nu_1T_1+nu_2T_2}{nu_1+nu_2}] По закону Клапейрона – Менделеева [p2V=left(nu_1+nu_2right)RT] Отсюда объем одного сосуда [V=dfrac{left( nu_1T_1+nu_2T_2right)R}{2p}=dfrac{left( 3text{ моль} cdot 350text{ К}+2text{ моль} cdot 400text{ К}right)cdot 8,31 text{ Дж/(моль$cdot$ К)}}{2cdot 6cdot 10^3 text{ Па}}approx 1,28text{ м$^3$ }]
Ответ: 1,28
1 моль идеального одноатомного газа сначала изотермически расширили. Затем изохорно нагрели, при этом его давление возросло в 3 раза (см. рисунок). Какое количество теплоты получил газ на участке 2–3, если (T_1=100) К? Ответ дайте в Дж.
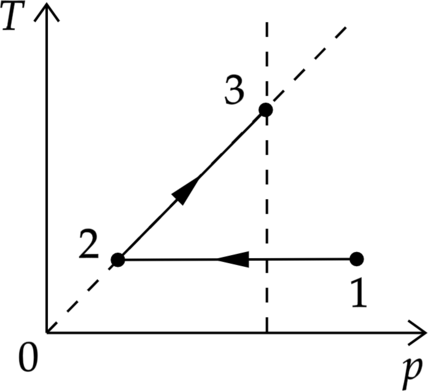
1. Воспользуемся первым законом термодинамики [Q=Delta U+A,] где (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии системы, (A) – работа газа.
Так как процесс изохорный, то работа газа равна 0. Распишем изменение внутренней энергии и получим [Q=dfrac{3}{2}nu R Delta T=dfrac{3}{2}nu R left(T_3-T_2right)] 2. Воспользуемся законом Шарля [dfrac{p_2}{T_2}=dfrac{p_3}{T_3} Rightarrow T_3=dfrac{p_3 T_2}{p_2}=3T_2] 3. По условию процесс 1–2 изотермический, значит [T_1=T_2] Следовательно, первый закон термодинамики выглядит [Q=dfrac{3}{2}nu R left(3T_1-T_1right)=3nu R T_1= 3cdot 1 text{ моль} cdot 8,31 text{ Дж/(моль $cdot$ К)}cdot 100text{ К}=2493text{ Дж}]
Ответ: 2493
Один моль одноатомного идеального газа совершает процесс 1–2–3, график которого показан на рисунке в координатах T–V, Известно, что в процессе 1–2 газ совершил работу 3 кДж, а в процессе 2–3 объём газа V увеличился в 2 раза. Какое количество теплоты было сообщено газу в процессе 1–2–3, если его температура Т в состоянии 3 равна 600 К? Ответ дайте в Дж.
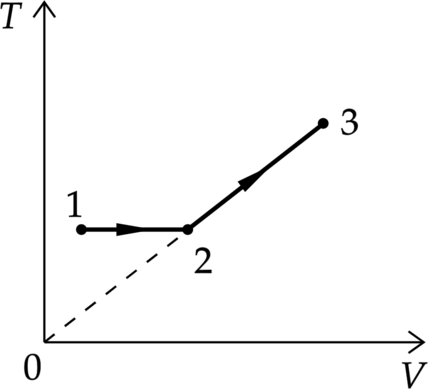
1.Проанализируем процессы
1–2 Процесс изотермический, по закон Бойля-Мариотта [p_1 V_1=p_2V_2] Значит возрастает объем и давление.
2–3 Температура увеличивается линейно объему, следовательно, процесс изобарный.
2. Количество теплоты, полученное в процессе 1–2–3, равно сумме количеств теплоты, полученных в процессах 1–2 и 2–3. [Q_{123}=Q_{12}+Q_{23}] 3. По первому закону термодинамики [Q=Delta U +A,] где (Q) – количество теплоты, полученное системой, (Delta U) – изменение внутренней энергии системы, (A) – работа газа.
Значит в процессе 1–2 изменение внутренней энергии равно 0, а количество теплоты [Q_{12}=A_{12}=3 text{ кДж}] В процессе 2–3 по условию объем возрос в 2 раза, значит по закону Гей-Люссака [dfrac{V_2}{T_2}=dfrac{V_3}{T_3}Rightarrow T_2=dfrac{V_2 T_3}{V_3}= dfrac{600text{ К}}{2}=300text{ К}] По закону Клапейрона–Менделеева [pV=nu R T] Значит количество теплоты, полученное в процессе 2–3 равно [Q_{23}=dfrac{3}{2}nu R left(T_3-T_2right)+pleft( V_3-V_2right)=dfrac{3}{2}nu R left(T_3-T_2right)+nu R left(T_3-T_2right)=dfrac{5}{2}nu R left(T_3-T_2right)] [Q_{23}=dfrac{5}{2}cdot 1 text{ моль} cdot 8,31 text{ Дж/(моль $cdot$ К)}left( 600 text{ К}- 300text{ К}right)= 6232,5 text{ Дж}] А общее количество теплоты [Q=Q_{12}+Q_{23}=6232,5 text{ Дж}+ 3000text{ Дж}=9232,5 text{ Дж}]
Ответ: 9232,5
На рисунке показан циклический процесс постоянное количество одноатомного газа. Работу, которую совершают внешние силы при переходе газа из состояния 2 в состояние 3, равна 5 кДж. Какое количество теплоты газ отдаёт за цикл холодильнику? Ответ дайте в кДж 
Работа внешних сил в процессе 2–3 равна площади под графиком. [A_{23}=dfrac{p_0+2p_0}{2}left(3V_0-V_0right)=3p_0V_0] (p) – давление, (V) – объем газа, (nu) – количество вещества, (T) – температура газа в Кельвинах.
Воспользуемся первым законом термодинамики [|Q_{text{ хол}}|=|Q_{23}|=Delta U_{23}+A_{32}=dfrac{3}{2}left( nu R T_2 -nu R T_3right)+ 3p_0V_0quad (1)] Также по уравнению Клапейрона – Менделеева [p_2V_2=nu R T_2= 2p_0 cdot 3V_0 =6p_0V_0 quad (2)] [p_2V_2=nu R T_3=p_0V_0 quad (3)] Подставим в (1) формулы (2) и (3) [|Q_{text{ хол}}|=dfrac{3}{2}left(6p_0V_0-p_0V_0right)+3p_0V_0= dfrac{21}{2}p_0V_0=dfrac{7}{2}A_{23}=3,5 cdot 5text{ кДж} =17,5text{ кДж}]
Ответ: 17,5
Источник