Один моль идеального одноатомного газа совершает цикл состоящий из двух изохор
Условие задачи:
Один моль одноатомного газа совершает цикл, состоящий из двух изохор и двух изобар. При этом максимальное давление в 2 раза больше минимального, а максимальный объем в 3 раза больше минимального. Определите коэффициент полезного действия цикла.
Задача №5.5.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(nu=1) моль, (p_2=2p_1), (V_2=3V_1), (eta-?)
Решение задачи:
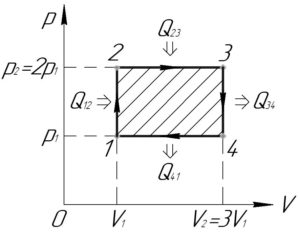Изобразим цикл, совершаемый над газом, в координатах p-V (смотрите схему).
КПД цикла (eta) определяют по формуле:
[eta = frac{A}{{{Q_н}}};;;;(1)]
Работа газа в цикле (A) равна площади цикла в координатах p-V, при этом если цикл обходится по часовой стрелке (как у нас), то работа цикла положительна.
[A = left( {{p_2} – {p_1}} right)left( {{V_2} – {V_1}} right)]
Так как по условию (p_2=2p_1) и (V_2=3V_1), то:
[A = left( {2{p_1} – {p_1}} right)left( {3{V_1} – {V_1}} right) = 2{p_1}{V_1};;;;(2)]
Отлично! Теперь, чтобы найти количество теплоты (Q_н), нужно определить все процессы в цикле, в которых тепло подводилось к газу. Для начала запишем первый закон термодинамики, мы к нему будем постоянно обращаться:
[Q = Delta U + A;;;;(3)]
Изменение внутренней энергии одноатомного идеального газа (Delta U) определяют по формуле:
[Delta U = frac{3}{2}nu RDelta T;;;;(4)]
Работу газа (A) можно определить следующим образом:
[A = pDelta V;;;;(5)]
Также запишем уравнение Клапейрона-Менделеева для состояния газа в точках 1-4. В уравнениях сразу учтём, что (p_2=2p_1) и (V_2=3V_1).
[left{ begin{gathered}
{p_1}{V_1} = nu R{T_1} ;;;;(6)hfill \
2{p_1}{V_1} = nu R{T_2} ;;;;(7)hfill \
2{p_1} cdot 3{V_1} = nu R{T_3} ;;;;(8)hfill \
{p_1} cdot 3{V_1} = nu R{T_4} hfill \
end{gathered} right.]
Рассмотрим процесс 1-2, который является изохорным ((V=const)), значит работа газа (A_{12}) в этом процессе равна нулю (так как (Delta V_{12}=0)). Поэтому количество теплоты (Q_{12}) по формуле (3) равно:
[{Q_{12}} = Delta {U_{12}}]
Тогда согласно формуле (4), имеем:
[{Q_{12}} = frac{3}{2}nu RDelta {T_{12}};;;;(9)]
Так как в этом изохорном процессе давление увеличивается, значит по закону Шарля температура также растёт ((Delta T_{12}>0)). Поэтому из формулы (9) следует, что тепло в процессе 1-2 подводилось ((Q_{12}>0)). Отнимем из уравнения (7) уравнение (6):
[{p_1}{V_1} = nu Rleft( {{T_2} – {T_1}} right)]
[{p_1}{V_1} = nu RDelta {T_{12}}]
Тогда формула (9) примет такой вид:
[{Q_{12}} = frac{3}{2}{p_1}{V_1};;;;(10)]
Если провести аналогичные рассуждения для изохорного процесса 3-4, то Вы выясните, что (Q_{34}<0), то есть тепло в этом процессе отводилось от газа.
Также рассмотрим изобарный процесс 2-3 ((p=const)). Количество теплоты (Q_{12}) согласно формуле (3) равно:
[{Q_{23}} = Delta {U_{23}} + {A_{23}};;;;(11)]
Изменение внутренней энергии (Delta U_{23}) по формуле (4) равно:
[Delta {U_{23}} = frac{3}{2}nu RDelta {T_{23}};;;;(12)]
Работа газа (A_{23}) согласно формуле (5) равна:
[{A_{23}} = {p_2} cdot left( {{V_2} – {V_1}} right) = {p_2}{V_2} – {p_2}{V_1}]
Так как в условии сказано, что (p_2=2p_1) и (V_2=3V_1), то:
[{A_{23}} = 2{p_1} cdot 3{V_1} – 2{p_1}{V_1}]
Учитывая уравнения (7) и (8), имеем:
[{A_{23}} = nu R{T_3} – nu R{T_2}]
[{A_{23}} = nu RDelta {T_{23}};;;;(13)]
Подставив выражения (12) и (13) в формулу (11), получим:
[{Q_{23}} = frac{3}{2}nu RDelta {T_{23}} + nu RDelta {T_{23}}]
[{Q_{23}} = frac{5}{2}nu RDelta {T_{23}};;;;(14)]
Так как в изобарном процессе 2-3 объем увеличивался, значит по закону Гей-Люссака его температура росла ((Delta T_{23}>0)). Поэтому из формулы (14) следует, что тепло в процессе 2-3 подводилось ((Q_{23}>0)). Отнимем из уравнения (8) уравнение (7):
[4{p_1}{V_1} = nu Rleft( {{T_3} – {T_2}} right)]
[4{p_1}{V_1} = nu RDelta {T_{23}}]
Тогда формула (14) примет такой вид:
[{Q_{23}} = frac{5}{2} cdot 4{p_1}{V_1}]
[{Q_{23}} = 10{p_1}{V_1};;;;(15)]
Проведя аналогичные рассуждения для изобарного процесса 4-1, Вы выясните, что (Q_{41}<0), то есть тепло в этом процессе отводилось от газа.
В ходе наших рассуждений мы выяснили, что к газу теплота подводится только в процессах 1-2 и 2-3, то есть количество теплоты (Q_н) равно:
[{Q_н} = {Q_{12}} + {Q_{23}}]
Примем во внимание полученные равенства (10) и (15), тогда:
[{Q_н} = frac{3}{2}{p_1}{V_1} + 10{p_1}{V_1}]
[{Q_н} = frac{{23}}{2}{p_1}{V_1};;;;(16)]
Тогда согласно формуле (1) коэффициент полезного действия цикла (eta), учитывая выражения (2) и (16), равен:
[eta = frac{{2{p_1}{V_1}}}{{frac{{23}}{2}{p_1}{V_1}}} = frac{4}{{23}} = 0,174]
Ответ: 0,174.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 1493
Моль идеального одноатомного газа совершает замкнутый цикл, состоящий из трех процессов: адиабатического расширения 1-2, изотермического сжатия 2-3 и изохорического нагревания 3-1 (см. рисунок). Какая работа была совершена газом в адиабатическом процессе, если в процессе изохорного нагревания газу подведено тепло $Q_{31} = 10 кДж$?
Подробнее
Задача по физике – 1494
Моль идеального газа охлаждается при постоянном объеме, а затем при постоянном давлении приводится в состояние с температурой, равной начальной $T_{0} = 300 К$. В итоге газ получил тепло $Q = 1500 Дж$. Во сколько раз конечное давление отличается от начального?
Подробнее
Задача по физике – 1495
Цикл, совершаемый некоторой массой идеального одноатомпого газа, состоит из двух изохор и двух изобар. Известно, что наибольшее давление в два раза больше наименьшего, а наибольший объем в четыре раза больше наименьшего в данном процессе. Найти КПД цикла.
Подробнее
Задача по физике – 1496
Поршень массы $M$, замыкающий объем $V_{0}$ идеального одноатомного газа при давлении $P_{0}$ и температуре $T_{0}$, движется со скоростью $v$. Определить температуру газа при максимальном сжатии. Теплообменом пренебречь.
Подробнее
Задача по физике – 1497
В горизонтальном неподвижном цилиндрическом сосуде, закрытом поршнем массы М, находится моль идеального одноатомного газа. Газ нагревают. Поршень, двигаясь равноускоренно, приобретает скорость v. Сколько тепла подведено газу? Теплоемкостью сосуда и поршня, а также внешним давлением пренебречь.
Подробнее
Задача по физике – 1498
Моль газа участвует в циклическом процессе, график которого состоит из двух изохор и двух изобар (см. рис.) Температуры газа в точках 1 и 3 равны соответственно $T_{1}$ и $T_{3}$. Определить работу, совершенную газом за цикл, если известно, что точки 2 и 4 лежат на одной изотерме.
Подробнее
Задача по физике – 1499
Найти теплоемкость системы, состоящей из перекрытого поршнем сосуда с одноатомным газом (параметры $P_{0}, V_{0}, T_{0}$). Поршень удерживается пружиной. Слева от поршня вакуум. Если газ откачать, поршень соприкоснется с правой стенкой сосуда, а пружина будет недеформирована. Теплоемкостями сосуда, поршня и пружины пренебречь.
Подробнее
Задача по физике – 1500
Из небольшого отверстия в баллоне со сжатым гелием вытекает струя газа со скоростью $v$. Найти разность температур гелия в баллоне и в струе. Давление в струе считать равным внешнему давлению, скоростью газа в баллоне при расчетах пренебречь.
Подробнее
Задача по физике – 1501
Какую работу надо совершить, чтобы каплю жидкости объемом $V$ с поверхностным натяжением $sigma$ растянуть в пленку, толщина которой $d$ мала по сравнению с первоначальным радиусом капли?
Подробнее
Задача по физике – 1502
Найти поверхностное натяжение жидкости, если петля из резиновой нити длины $l_{0}$ и жесткости $k$, положенная на пленку этой жидкости, растянулась до окружности радиуса $R$ после прокола пленки внутри петли.
Подробнее
Задача по физике – 1503
Железный кубик, смазанный парафином, плавает в воде так, что его верхняя грань находится на уровне воды. Вода не смачивает парафин. Найти длину ребра кубика.
Подробнее
Задача по физике – 1504
Определить толщину слоя жидкости, разлитой па горизонтальной плоскости. Краевой угол $theta$, плотность жидкости $rho$, поверхностное натяжение $sigma$.
Подробнее
Задача по физике – 1505
Вычислить давление жидкости под ее сферической поверхностью радиуса $R$, вызванного силами поверхностного натяжения. Коэффициент $sigma$ известен.
Подробнее
Задача по физике – 1506
Вычислить давление внутри мыльного пузыря радиуса $R$. Коэффициент поверхностного натяжения $sigma$, внешнее давление отсутствует.
Подробнее
Задача по физике – 1507
Найти радиус кривизны капли в ее верхней точке А. Масса капли $M$, ее высота $H$, радиус соприкосновения капли с горизонтальной плоскостью, на которой она находится, равен $r$. Плотность жидкости $rho$, поверхностное натяжение $sigma$. Плоскость не смачивается жидкостью.
Подробнее
Источник
А.И.Фридман,
школа № 7, г. Москва
Методика решения задач с
использованием диаграмм состояния
10-й класс. углубленный
курс
Метод решения задач с
использованием диаграмм состояния успешно
зарекомендовал себя при изуче- нии тем «Газовые
законы», «Термодинамика», «Тепловые двигатели».
Этот метод может быть использован также и на
уроках, и на факультативных занятиях.
1. При нагревании газа получена
зависимость, показанная на рисунке. Определите,
сжимался газ или расширялся? [Масса газа
постоянна. – Ред.]
Решение
Нужно провести из начала
координат прямые (пунктир на чертеже),
проходящие через состояния 1 и 2.
Эти прямые соответствуют процессам при
постоянных объемах V1 и V2.
Поскольку V2 > V1, газ
расширялся.
2. Как менялась температура
[заданной массы. – Ред.] идеального газа
(увеличивалась или уменьшалась) в процессе,
график которого в координатах p, V изображен
на рисунке?
Решение
Проведем гиперболы,
касательные к кривой. Так как гипербола в
координатах p, V является графиком изотермы:
pV = nRT
= const, то T1 < T2. Следовательно, от
состояния 1 до состояния 2 температура газа
повышалась, а от состояния 2 до состояния 1 –
понижалась.
3. Получены две
экспериментальные зависимости (см. рисунок). В
каком случае масса газа больше? Давление в первом
и во втором случае одинаково.
Решение
Так как V1 > V2,
то m1 > m2.
4. Над идеальным газом производят
два замкнутых процесса: 1–2–3–1 и 3–2–4–3.
В каком из них газ совершает бо1льшую работу?
Решение
Изобразим изменение
состояния газа на p–V-диаграмме.
Очевидно, что А2 > А1.
5. Моль идеального одноатомного
газа переводится из начального состояния 1 в
конечное состояние 4 в ходе процесса 1–2–3–4.
определите подведенное к газу количество
теплоты, если разность начальной и конечной
температур DT = 100 К. Считать R = 8,3 Дж/(моль • К).
Решение
Из р–Т-диаграммы
видно, что T2 – T1 = T4 – T3
= DТ.
Воспользуемся формулой Q = DU + A ‘:
– тепло подводится;
– тепло отводится, T уменьшается;
– тепло подводится.
6. Моль одноатомного [идеального.
– Ред.] газа совершает замкнутый цикл,
состоящий из трех процессов: адиабатического
расширения, изотермического сжатия и изохорного
нагревания. Какая работа была совершена газом в
адиабатическом процессе, если при изохорном
нагревании подвели Q = 10 кДж тепла? R = 8,3 Дж/(К • моль).
[Для произвольного идеального газа результат тот
же. – Ред.]
Решение
Q12 = 0 Ю = –DU12 .
T2 = T3Ю – DU31 = DU12.
V1 = V3Ю Q31 = DU31 = 10 кДж,
т.к. A’31 = 0.
Таким образом, A ’12 = –DU12 = DU31 = Q31 =
10 кДж.
7. Один моль одноатомного
идеального газа совершает замкнутый цикл,
состоящий из процесса с линейной зависимостью
давления от объема, изобары и изохоры. Найдите
количество теплоты, подведенное к газу на
участках цикла, где его температура растет.
Температура газа в состояниях 1 и 2 равна
300 К. Отношение объемов на изобаре
Направление обхода цикла
указано стрелками. R = 8,3 Дж/(моль • К).
Решение
б) На участке 1–2 p = a – bV, т.е.:
p1 = a – bV1;
p2 = a – bV2.
Решая систему, находим:
Таким образом,
Умножив обе части на V,
получим:
На участке 1–4 температура
растет!
в)
Qподвед = Q31 + Q14 = 1245
Дж + 726,25 Дж d 1970 Дж.
8. Состояние [одного моля
идеального одноатомного. – Ред.] газа
меняется, как представлено на диаграмме p, T,
причем p ~ T на участке 1–2 и на участке 2–3. Найдите теплоемкости газа
на участках 1–2 и 2–3.
Решение
а) На участке 1–2
б) На участке 2–3 таким
образом, V ~ p. Работа газа в этом
случае:
[В решении этой задачи помещен
рисунок, предложенный редакцией, т.к. авторский
рисунок ошибочен. – Ред]
9. КПД тепловой машины,
работающей по циклу, состоящему из изотермы 1–2,
изохоры 2–3 и адиабаты 3–1, равен h. Разность
максимальной и минимальной температур газа в
цикле равна DT.
Найдите работу, совершенную n
молями одноатомного идеального газа в
изотермическом процессе.
Решение
Q12 – количество теплоты,
полученное от нагревателя; Q23 – количество
теплоты, отданное холодильнику; Q31 = 0,
т.к. 3–1 – адиабата.
Итак:
(адиабата);
(изотерма).
Поэтому
Задачи для
самостоятельного решения
1. Поршень в цилиндре с воздухом
прилегает к стенкам цилиндра неплотно, поэтому
медленно пропускает воздух. Снятая во время
нагревания при постоянном давлении зависимость
объема от температуры изображена на рисунке.
Увеличивалась или уменьшалась масса воздуха в
цилиндре? (Ответ. Масса газа в состоянии 1
больше, чем в состоянии 2.)
2. На рисунке показан
циклический процесс, проведенный над некоторой
массой [идеального. – Ред.] газа. Изобразите
этот процесс в координатах p, T и V, T (1–2
и 4–5 – изотермы).
3. На p–T-диаграмме изображен
замкнутый процесс, который совершает некоторая
масса кислорода. Известно, что максимальный
объем, который занимал газ в этом процессе, Vмакс = 16,6 дм3.
Определите массу газа и его объем в точке 1.
Значения T1, T2, p1 и p2
указаны на рисунке.
(Ответ. V1 = 12,4 дм3; m = 16 г.)
4. Найдите работу,
совершаемую молем идеального газа в цикле,
состоящем из двух участков линейной зависимости
давления от объема и изохоры. Точки 1 и 3
лежат на прямой, проходящей через начало
координат. Температуры в точках 2 и 3
одинаковы. Считать заданными температуры T1
и T2 в точках 1 и 2. (Ответ )
5. В тепловом процессе моль
[одноатомного. – Ред.] идеального газа
переводят из начального состояния в конечное,
как показано на рисунке. Какое количество
теплоты подведено к газу, если разность
начальной и конечной температур DT = 100 °C? (Ответ. 415 Дж.)
6. Моль идеального газа
переводят из состояния 1 в состояние 2: в
первом случае – адиабатически, а во втором –
сначала по изобаре 1–3, а затем по изохоре 3–2.
Минимальная температура Tмин = 300 К.
Количество теплоты, подведенное к газу в
процессе 1–3–2, равно 2,6 кДж. Чему
равна работа газа в адиабатическом процессе?
(Ответ. А12 = –
12 560 Дж.)
7. Один моль идеального газа
изменяет свое состояние согласно
представленному циклу. 1–4 и 2–3 – изохоры,
3–4 – изобара, 1–2 – прямая.
Температуры в состояниях 1, 2, 3, 4
равны соответственно T1, T2, T3,
T4. Какую работу совершает газ за один
цикл?
(Ответ. .)
8. В каждом из процессов,
изображенных на диаграмме, температура
изменяется на одну и ту же величину. В каком из
этих процессов газ получает наибольшее
количество теплоты? (Ответ. в изобарном
процессе.)
9. Состояние [моля идеального. – Ред.]
газа меняется, как представлено на диаграмме p, V,
причем p ~ V2 на участке 1–2.
Найдите теплоемкость газа в этом процессе. (Ответ. .)
[Авторский ответ ошибочен.
– Ред.]
4 10. Найдите КПД тепловых
машин, работающих по циклам 1–2–3–1 и 1–3–4–1,
если КПД машины, работающей по циклу 1–2–3–4–1,
равен h.
В качестве рабочего тела во всех слу-
чаях используется [один и тот
же. – Ред.] идеальный газ.
(Ответ: )
44 11. Определите КПД цикла,
состоящего из двух адиабат и двух изохор,
совершаемого одноатомным идеальным газом.
Известно, что в процессе адиабатного расширения
устанавливается температура T2 = 0,75 T1,
а в
процессе адиабатного сжатия T3 = 0,75 T4.
(Ответ: h = 25 %.)
[Для произвольного идеального
газа результат тот же. – Ред.]
Источник
А.И.Фридман,
школа № 7, г. Москва
Методика решения задач с
использованием диаграмм состояния
10-й класс. углубленный
курс
Метод решения задач с
использованием диаграмм состояния успешно
зарекомендовал себя при изуче- нии тем «Газовые
законы», «Термодинамика», «Тепловые двигатели».
Этот метод может быть использован также и на
уроках, и на факультативных занятиях.
1. При нагревании газа получена
зависимость, показанная на рисунке. Определите,
сжимался газ или расширялся? [Масса газа
постоянна. – Ред.]
Решение
Нужно провести из начала
координат прямые (пунктир на чертеже),
проходящие через состояния 1 и 2.
Эти прямые соответствуют процессам при
постоянных объемах V1 и V2.
Поскольку V2 > V1, газ
расширялся.
2. Как менялась температура
[заданной массы. – Ред.] идеального газа
(увеличивалась или уменьшалась) в процессе,
график которого в координатах p, V изображен
на рисунке?
Решение
Проведем гиперболы,
касательные к кривой. Так как гипербола в
координатах p, V является графиком изотермы:
pV = nRT
= const, то T1 < T2. Следовательно, от
состояния 1 до состояния 2 температура газа
повышалась, а от состояния 2 до состояния 1 –
понижалась.
3. Получены две
экспериментальные зависимости (см. рисунок). В
каком случае масса газа больше? Давление в первом
и во втором случае одинаково.
Решение
Так как V1 > V2,
то m1 > m2.
4. Над идеальным газом производят
два замкнутых процесса: 1–2–3–1 и 3–2–4–3.
В каком из них газ совершает бо1льшую работу?
Решение
Изобразим изменение
состояния газа на p–V-диаграмме.
Очевидно, что А2 > А1.
5. Моль идеального одноатомного
газа переводится из начального состояния 1 в
конечное состояние 4 в ходе процесса 1–2–3–4.
определите подведенное к газу количество
теплоты, если разность начальной и конечной
температур DT = 100 К. Считать R = 8,3 Дж/(моль • К).
Решение
Из р–Т-диаграммы
видно, что T2 – T1 = T4 – T3
= DТ.
Воспользуемся формулой Q = DU + A ‘:
– тепло подводится;
– тепло отводится, T уменьшается;
– тепло подводится.
6. Моль одноатомного [идеального.
– Ред.] газа совершает замкнутый цикл,
состоящий из трех процессов: адиабатического
расширения, изотермического сжатия и изохорного
нагревания. Какая работа была совершена газом в
адиабатическом процессе, если при изохорном
нагревании подвели Q = 10 кДж тепла? R = 8,3 Дж/(К • моль).
[Для произвольного идеального газа результат тот
же. – Ред.]
Решение
Q12 = 0 Ю = –DU12 .
T2 = T3Ю – DU31 = DU12.
V1 = V3Ю Q31 = DU31 = 10 кДж,
т.к. A’31 = 0.
Таким образом, A ’12 = –DU12 = DU31 = Q31 =
10 кДж.
7. Один моль одноатомного
идеального газа совершает замкнутый цикл,
состоящий из процесса с линейной зависимостью
давления от объема, изобары и изохоры. Найдите
количество теплоты, подведенное к газу на
участках цикла, где его температура растет.
Температура газа в состояниях 1 и 2 равна
300 К. Отношение объемов на изобаре
Направление обхода цикла
указано стрелками. R = 8,3 Дж/(моль • К).
Решение
б) На участке 1–2 p = a – bV, т.е.:
p1 = a – bV1;
p2 = a – bV2.
Решая систему, находим:
Таким образом,
Умножив обе части на V,
получим:
На участке 1–4 температура
растет!
в)
Qподвед = Q31 + Q14 = 1245
Дж + 726,25 Дж d 1970 Дж.
8. Состояние [одного моля
идеального одноатомного. – Ред.] газа
меняется, как представлено на диаграмме p, T,
причем p ~ T на участке 1–2 и на участке 2–3. Найдите теплоемкости газа
на участках 1–2 и 2–3.
Решение
а) На участке 1–2
б) На участке 2–3 таким
образом, V ~ p. Работа газа в этом
случае:
[В решении этой задачи помещен
рисунок, предложенный редакцией, т.к. авторский
рисунок ошибочен. – Ред]
9. КПД тепловой машины,
работающей по циклу, состоящему из изотермы 1–2,
изохоры 2–3 и адиабаты 3–1, равен h. Разность
максимальной и минимальной температур газа в
цикле равна DT.
Найдите работу, совершенную n
молями одноатомного идеального газа в
изотермическом процессе.
Решение
Q12 – количество теплоты,
полученное от нагревателя; Q23 – количество
теплоты, отданное холодильнику; Q31 = 0,
т.к. 3–1 – адиабата.
Итак:
(адиабата);
(изотерма).
Поэтому
Задачи для
самостоятельного решения
1. Поршень в цилиндре с воздухом
прилегает к стенкам цилиндра неплотно, поэтому
медленно пропускает воздух. Снятая во время
нагревания при постоянном давлении зависимость
объема от температуры изображена на рисунке.
Увеличивалась или уменьшалась масса воздуха в
цилиндре? (Ответ. Масса газа в состоянии 1
больше, чем в состоянии 2.)
2. На рисунке показан
циклический процесс, проведенный над некоторой
массой [идеального. – Ред.] газа. Изобразите
этот процесс в координатах p, T и V, T (1–2
и 4–5 – изотермы).
3. На p–T-диаграмме изображен
замкнутый процесс, который совершает некоторая
масса кислорода. Известно, что максимальный
объем, который занимал газ в этом процессе, Vмакс = 16,6 дм3.
Определите массу газа и его объем в точке 1.
Значения T1, T2, p1 и p2
указаны на рисунке.
(Ответ. V1 = 12,4 дм3; m = 16 г.)
4. Найдите работу,
совершаемую молем идеального газа в цикле,
состоящем из двух участков линейной зависимости
давления от объема и изохоры. Точки 1 и 3
лежат на прямой, проходящей через начало
координат. Температуры в точках 2 и 3
одинаковы. Считать заданными температуры T1
и T2 в точках 1 и 2. (Ответ )
5. В тепловом процессе моль
[одноатомного. – Ред.] идеального газа
переводят из начального состояния в конечное,
как показано на рисунке. Какое количество
теплоты подведено к газу, если разность
начальной и конечной температур DT = 100 °C? (Ответ. 415 Дж.)
6. Моль идеального газа
переводят из состояния 1 в состояние 2: в
первом случае – адиабатически, а во втором –
сначала по изобаре 1–3, а затем по изохоре 3–2.
Минимальная температура Tмин = 300 К.
Количество теплоты, подведенное к газу в
процессе 1–3–2, равно 2,6 кДж. Чему
равна работа газа в адиабатическом процессе?
(Ответ. А12 = –
12 560 Дж.)
7. Один моль идеального газа
изменяет свое состояние согласно
представленному циклу. 1–4 и 2–3 – изохоры,
3–4 – изобара, 1–2 – прямая.
Температуры в состояниях 1, 2, 3, 4
равны соответственно T1, T2, T3,
T4. Какую работу совершает газ за один
цикл?
(Ответ. .)
8. В каждом из процессов,
изображенных на диаграмме, температура
изменяется на одну и ту же величину. В каком из
этих процессов газ получает наибольшее
количество теплоты? (Ответ. в изобарном
процессе.)
9. Состояние [моля идеального. – Ред.]
газа меняется, как представлено на диаграмме p, V,
причем p ~ V2 на участке 1–2.
Найдите теплоемкость газа в этом процессе. (Ответ. .)
[Авторский ответ ошибочен.
– Ред.]
4 10. Найдите КПД тепловых
машин, работающих по циклам 1–2–3–1 и 1–3–4–1,
если КПД машины, работающей по циклу 1–2–3–4–1,
равен h.
В качестве рабочего тела во всех слу-
чаях используется [один и тот
же. – Ред.] идеальный газ.
(Ответ: )
44 11. Определите КПД цикла,
состоящего из двух адиабат и двух изохор,
совершаемого одноатомным идеальным газом.
Известно, что в процессе адиабатного расширения
устанавливается температура T2 = 0,75 T1,
а в
процессе адиабатного сжатия T3 = 0,75 T4.
(Ответ: h = 25 %.)
[Для произвольного идеального
газа результат тот же. – Ред.]
Источник