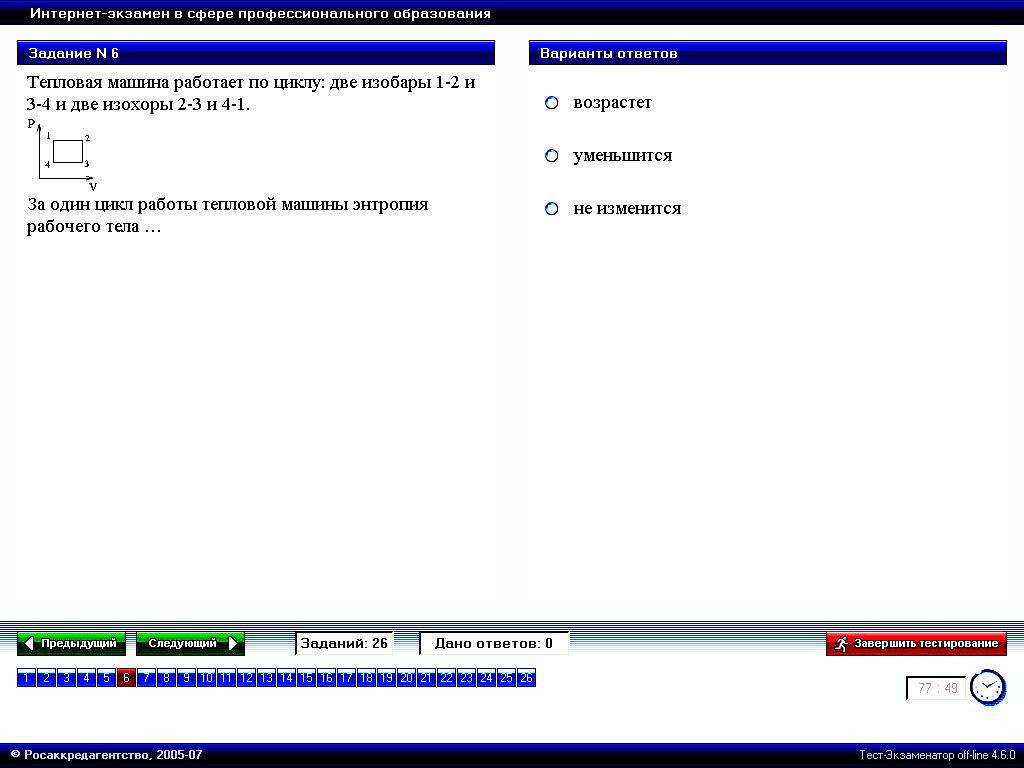
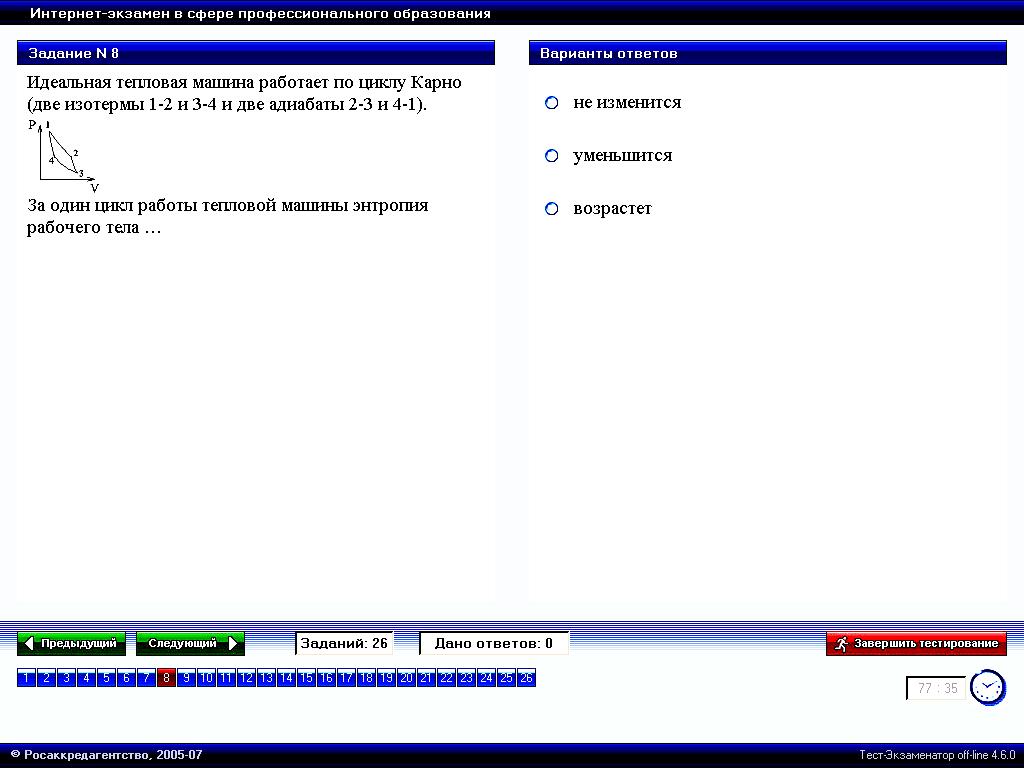
На рисунке представлен цикл тепловой машины в координатах t s где s энтропия
2.3.4-2
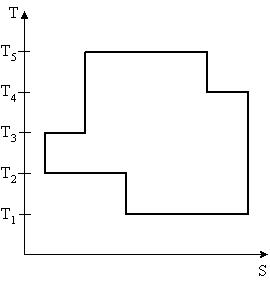
На рисунке представлен цикл тепловой машины в координатах T, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами.
| 1:Нагреватели – T3,T4,T5 Холодильники – T1,T2* 2:Нагреватели – T4,T5 Холодильники – T1,T2,T3 3:Нагреватели – T2,T3,T5 Холодильники – T1,T4 4:Нагреватели – T3,T5 Холодильники – T1,T2,T4 |
Будем считать, что цикл осуществляется в направлении, указанном на рисунке стрелками. Теплообмен происходит при изотермическом процессе (T-const). .
Q>0 (подводится тепло – нагреватель),S – возрастает, Q<0 (отводится тепло – холодильник), S – убывает. Таким образом, Q>0 при T3,T4,T5; Q<0 при T1,T2
Ответ: 1
2.3.4-3
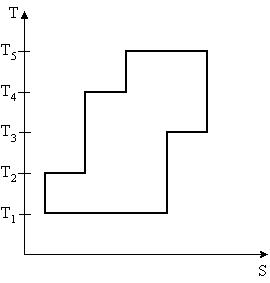
На рисунке представлен цикл тепловой машины в координатах T, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами.
| 1:Нагреватели – T2,T4,T5 Холодильники – T1,T3* 2:Нагреватели – T4,T5 Холодильники – T1,T2,T3 3:Нагреватели – T3,T4,T5 Холодильники – T1,T2 4:Нагреватели – T2,T4 Холодильники – T1,T3,T5 |
Будем считать, что цикл осуществляется в направлении, указанном на рисунке стрелками. Теплообмен происходит при изотермическом процессе (T-const). . Q>0(подводится тепло – нагреватель),S – возрастает, Q<0(отводится тепло – холодильник), S – убывает. Таким образом, Q>0 при T2,T4,T5; Q<0 при T1,T3
Ответ: 1
2.3.4-4
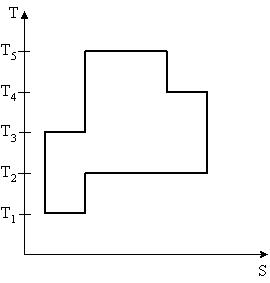
На рисунке представлен цикл тепловой машины в координатах T, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами.
| 1:Нагреватели – T3,T4,T5 Холодильники – T1,T2* 2:Нагреватели – T4,T5 Холодильники – T1,T2,T3 3:Нагреватели – T3,T5 Холодильники – T1,T2,T4 4:Нагреватели – T2,T4,T5 Холодильники – T1,T3 |
Будем считать, что цикл осуществляется в направлении, указанном на рисунке стрелками. Теплообмен происходит при изотермическом процессе (T-const). . Q>0(подводится тепло – нагреватель),S – возрастает, Q<0(отводится тепло – холодильник), S – убывает. Таким образом, Q>0 при T3,T4,T5; Q<0 при T1,T2.
Ответ: 1
2.3.4-5
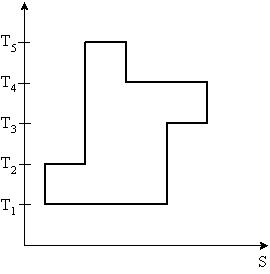
На рисунке представлен цикл тепловой машины в координатах T, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами.
| 1:Нагреватели – T2,T4,T5 Холодильники – T1,T3* 2:Нагреватели – T4,T5 Холодильники – T1,T2,T3 3:Нагреватели – T2,T5 Холодильники – T1,T3,T4 4:Нагреватели – T3,T4,T5 Холодильники – T1,T2 |
Б удем считать, что цикл осуществляется в направлении, указанном на рисунке стрелками. Теплообмен происходит при изотермическом процессе (T-const). . Q>0 (подводится тепло – нагреватель),S – возрастает, Q<0 (отводится тепло – холодильник), S – убывает. Таким образом, Q>0 при T2,T4,T5; Q<0 при T1,T3.
Ответ: 1
2.3.5-1
Газ находится в состоянии с параметрами P1,V1. Необходимо расширить газ, затратив при этом минимум энергии. Для этого подходит процесс … | 1. изотермический* 2. изобарический 3. ни один процесс не подходит 4. изохорический 5. адиабатический* |
Изотермический, т.к. при этом процессе =0, а Q=A, следовательно, затрачивается минимум энергии. Или адиабатический, т.к. расширение происходит за счет внутренней энергии.
Ответ: 1 или 5
2.3.6-1
Тепловая машина работает по циклу: две изобары 1-2 и 3-4 и две изохоры 2-3 и 4-1.
За один цикл работы тепловой машины энтропия рабочего тела … | 1. возрастёт 2. уменьшится 3. не изменится* |
Энтропия является функцией состояния и за цикл начальное и конечное состояния совпадают, поэтому изменение энтропии равно нулю.
2.3.7-1
Идеальная тепловая машина работает по циклу Карно (две изотермы 1-2 и 3-4 и две адиабаты 2-3 и 4-1).
За один цикл работы тепловой машины энтропия рабочего тела … | 1. не изменится* 2. уменьшится 3. возрастёт |
Энтропия является функцией состояния и за цикл начальное и конечное состояния совпадают, поэтому изменение энтропии равно нулю.
2.3.8-1
Тепловая машина работает по циклу Карно. Если температуру нагревателя увеличить, то КПД цикла… | 1: увеличится* 2: не изменится 3: уменьшится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника. Если T1 – увеличится, то – уменьшится, и – увеличится. Следовательно, при увеличении температуры нагревателя КПД цикла также увеличится.
Ответ: 1
2.3.8-2
Тепловая машина работает по циклу Карно. Если температуру нагревателя уменьшить, то КПД цикла… | 1: уменьшится* 2: увеличится 3: не изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника. Если T1 – уменьшится, то – увеличится, и – уменьшится. Следовательно, при уменьшении температуры нагревателя КПД цикла также уменьшится.
Ответ: 1
2.3.8-3
Тепловая машина работает по циклу Карно. Если температуру холодильника увеличить, то КПД цикла… | 1: уменьшится* 2: увеличится 3: не изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника. Если T2 – увеличится, то – увеличится, и – уменьшится. Следовательно, при уменьшении температуры нагревателя КПД цикла также уменьшится.
Ответ: 1
2.3.8-4
Тепловая машина работает по циклу Карно. Если температуру холодильника уменьшить, то КПД цикла… | 1: увеличится* 2: уменьшится 3: е изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника. Если T2 – уменьшится, то – уменьшится, и – увеличится. Следовательно, при уменьшении температуры нагревателя КПД цикла также увеличится.
Ответ: 1
2.3.8-5
Тепловая машина работает по циклу Карно. Если температуру нагревателя и холодильника увеличить на одинаковую величину ΔT, то КПД цикла… | 1: уменьшится* 2: увеличится 3: не изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника
Значит, если температуру нагревателя и холодильника увеличить на одинаковую величину ΔT, т.е. и , , . Следовательно, при увеличении температуры нагревателя и холодильника на одинаковую величину ΔT, КПД цикла уменьшится.
2.3.8-6
Тепловая машина работает по циклу Карно. Если температуру нагревателя и холодильника уменьшить на одинаковую величину ΔT, то КПД цикла… | 1: увеличится* 2: уменьшится 3: не изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника.
Значит, если температуру нагревателя и холодильника уменьшить на одинаковую величину ΔT, т.е. и , , . Следовательно, при уменьшении температуры нагревателя и холодильника на одинаковую величину ΔT, КПД цикла увеличится.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
90
7. Молярные теплоемкости идеального газа в про-
цессах 1→2 и 1→3 равны С1 и С2 соответственно. Их разность С2 – С1 имеет наиболь-
шую величину … .
а) для одноатомного газа б) для двухатомного газа в) для трехатомного газа
г) для любого идеального газа разность С2 – С1 оди-
накова
Ответ: г)
11.ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
11.1.Частные формулировки второго начала термодинамики
11.2.Энтропия и общая формулировка второго начала термодинамики
Второе начало термодинамики позволяет определить направление протекания процесса в изолированной системе.
11.1. Процесс перехода системы из состояния 1 в состояние 2 называют обратимым, если возвращение этой системы в исходное состояние через те же промежуточные состояния, что и в прямом процессе, но в обратной последовательности, можно осуществить без каких бы то ни было изменений в окружающих внешних телах. Всякий равновесный процесс является обратимым. Процесс перехода системы из состояния 1 в 2 называют необратимым, если обратный переход системы из 2 в 1 нельзя осуществить без изменений в окружающих телах. Все неравновесные (реальные) процессы необратимы. Рассмотрим примеры простейших необратимых процессов в изолированной систе-
91
ме. Это позволит получить частные формулировки второго начала термодинамики.
1. Рассмотрим теплоизолированный металлический стержень, исходная температура которого равна Т.
m , c, T
Предположим, что левая половина стержня самопроизвольно нагрелась до температуры T1 , а правая –
охладилась до температуры T2 . Опыт показывает, что хотя
первое начало термодинамики не запрещает этот процесс (необходимо лишь, чтобы выполнялось следующее соотношение между температурами Т1,Т2 и Т:
cmT c | m | T | c | m | T | и T T | 2T ), | |
2 | 1 | 2 | 2 | 1 | 2 | |||
он невозможен.
Первая частная формулировка второго начала тер-
модинамики: невозможны такие процессы, единствен-
ным конечным результатом которых был бы переход теплоты от тела менее нагретого к телу более нагре-
тому (постулат Клаузиуса).
2. Пусть мы имеем сосуд с газом. Допустим, что все молекулы газа собрались в одной из половин сосуда. Можно показать, что первому началу термодинамики этот
процесс не противоречит, но в природе такие процессы не наблюдаются.
Вторая частная формулировка второго начала тер-
модинамики: самопроизвольное «сжатие» газа в изолированной системе невозможно.
3. Третья частная формулировка второго начала термодинамики: невозможно построить такую перио-
92
дически действующую тепловую машину, которая, получив извне некоторое количество теплоты при любой температуре, полностью превращала бы ее в механическую работу и при этом возвращалась бы точно в ис-
ходное состояние (постулат Кельвина).
Устройство, которое периодически полностью превращало бы в работу получаемую извне теплоту, называют вечным двигателем II рода.
Частная формулировка второго начала термодинамики, предложенная Оствальдом: вечный двигатель II ро-
да невозможен.
Математическую формулировку второго начала можно получить, анализируя работу идеального теплового двигателя, совершающего в процессе работы обратимый цикл. Циклом или круговым процессом называют замкнутый процесс, в ходе которого система возвращается в исходное состояние.
Пусть рабочее тело тепловой машины т.е. тело, периодически изменяющее свои параметры, обычно – пар или газ, за каждый цикл получает количество теплоты Q1
от нагревателя, имеющего температуру T1 , и отдает коли-
чество теплоты Q2 хо- | |||
1 p1V1T1 Q1 | лодильнику, имеющему | ||
температуру | |||
a | 2p2V2T1 | T2 ( T2 T1 ). Обратимый | |
цикл, совершаемый теп- | |||
4 | б | ловой машиной в | этих |
p4V4T2 | 3p V T | условиях, может состоять | |
3 3 2 | как из процессов, в ходе | ||
Q2 | которых рабочее | тело | |
обменивается теплотой | |||
Рис. 20 | с нагревателем и холодильни- | ||
ком, так и из процессов, не сопровождающихся теплооб-
93
меном с внешней средой, т.е. адиабатических процессов. Процесс, сопровождающийся обменом теплотой, может быть обратимым только в том случае, если это равновес-
ный изотермический процесс, протекающий при темпе-
ратуре нагревателя или холодильника. Итак, обратимый цикл, совершаемый рабочим телом, вступающим в теплообмен с двумя телами бесконечно большой теплоемкости, может состоять из двух изотерм (при температурах нагревателя и холодильника) и двух адиабат. Этот идеальный обратимый цикл называют циклом Карно (рис. 20).
Для того чтобы сформулировать второе начало термодинамики в общем виде, необходимо ввести новую функцию состояния, которая называется энтропией.
11.2. Из анализа цикла Карно следует, что для обратимых процессов, примером которых являются равновес-
ные процессы, | Qобр | 0 , т.е. | Qобр | dS , |
Т | Т |
где S является функцией состояния, которую называют энтропией; Qобр – элементарное количество теплоты, пере-
данное системе в обратимом процессе.
Изменение энтропии вычисляют по формуле
Вычислим S для некоторых процессов.
1. Изменение состояния идеального газа
(p1V1T1→p2V2T2).
Так как Qобр dU A,будем иметь:
2 | dU A | 2 | m | dT | 2 | pdV | m | T | m | V | ||||
S | 2 | 2 | ||||||||||||
CV | CV ln | R ln | . | |||||||||||
T | M | T | T | M | T | M | V | |||||||
1 | 1 | 1 | 1 | 1 | ||||||||||
При обратимом адиабатическом процессе δQобр = 0
94
и S = const, поэтому такой процесс называют изоэнтропийным.
2. Изменение энтропии при нагревании или охлаждении твердых или жидких тел:
V 0 , A 0 , Q dU cmdT
2 Qобр | 2 | dT | T | ||
S | cm | 2 | . | ||
cm ln | |||||
T | T | T | |||
1 | 1 | 1 | |||
3. Изменение энтропии при изменении агрегатного состояния вещества
T const , Qобр dm ,
Как видно из рассмотренных примеров, энтропия неизолированной системы может, как увеличиваться, так и уменьшаться.
Однако энтропия изолированной системы ведет себя всегда однозначно: она не может уменьшаться, т.е. либо увеличивается, либо не изменяется. Это постулат, который называют вторым началом термодинамики:
Sизол. 0 . сист.
При этом энтропия отдельных частей системы может и увеличиваться и уменьшаться, но полная энтропия системы не убывает.
Максимально возможное значение энтропия изолированной системы достигает в состоянии теплового равновесия. Поскольку все естественные, самопроизвольные процессы необратимы, энтропия при этих процессах в изолированных системах всегда возрастает. Таким образом, второе начало термодинамики указывает направление протекания естественных процессов: естественные процессы в изолированных (или только адиабатно изолированных) си-
96
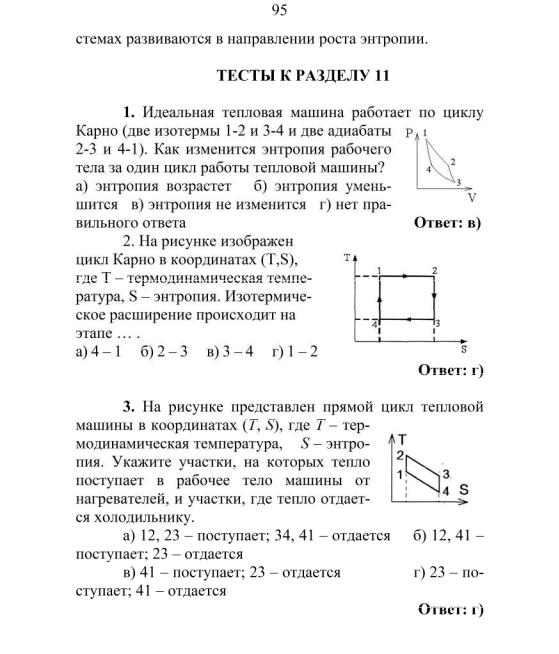
4. На рисунке представлен прямой цикл тепловой машины в координатах (T, S), где T – термодинамическая температура, S – энтропия.
Укажите участки, на которых тепло поступает в рабочее тело машины от нагревателей, и участки, где тепло отдается холодильнику.
а) 12, 23 – поступает; 31 – отдается; б) 12 – поступает; 23, 31 – отдается; в) 23 – поступает; 31 – отдается; г) 12 – поступает; 23 – отдается
Ответ: в) 5. На рисунке представлен прямой цикл тепловой
машины в координатах (T, S), где T – термодинамическая температура, S – энтропия. Укажите участки, на которых тепло поступает в рабочее тело машины от нагревателей, и участки, где тепло отдается холодильнику.
а) 23 – поступает; 41 – отдается б) 12 – поступает; 34, 41 – отдается в) 12, 23 – поступает; 34, 41 – отдается г) 12, 41 – поступает; 34 – отдается
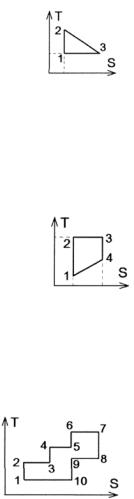
Ответ: а) 6. На рисунке представлен прямой цикл тепловой
машины в координатах (T, S), где T –
термодинамическая температура, S – энтропия. Укажите участки, на которых тепло поступает в рабочее тело машины от нагревателей, и участки, где тепло отдается холодильнику.
а) 12, 34, 56 – поступает; 78, 910 – отдается; б) 23, 45, 67 – поступает; 89, 101 – отдается;
в) 12, 23, 34, 45, 56, 67 – поступает; 78, 89, 910, 101 – отдает-
ся;
97
г) 78, 89, 910, 101 – поступает; 12, 23, 34, 45, 56, 67 – отдается
Ответ: б) 7. Один моль идеального газа находится в состоя-
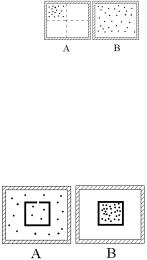
нии А, когда все молекулы собрались в левой верхней четверти теплоизолированного сосуда. Как изменится энтропия этого
газа, когда газ перейдет в состояние В, когда все молекулы разлетятся по всему сосуду?
а) энтропия возрастет | б) энтропия уменьшится |
в) энтропия не изменится | г) нет правильного ответа |
Ответ: а) |
8. В большом теплоизолированном сосуде находится один моль идеального газа и маленький сосуд с отверстием (состояние А). Как изменится энтропия газа, если в результате маловероятного процесса все молекулы соберутся в маленьком сосуде
(состояние В)? | |
а) энтропия возрастет | б) энтропия уменьшится |
в) энтропия не изменится | г) нет правильного ответа |
Ответ: б) |
12.ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
12.1.Средняя энергия молекулы. Внутренняя энергия идеального газа
12.2.Давление идеального газа с точки зрения молекулярно-кинетической теории
Системы с большим числом хаотически движущихся частиц подчиняются статистическим законам. Рассмотрим с этой точки зрения идеальный газ.
12.1. С помощью функции распределения газовых молекул по значениям скорости, которое будет рассмотре-
98
но ниже, можно вычислить среднее значение квадрата скорости молекул, а с его помощью и среднюю энергию поступательного движения газовых молекул:
K | mV 2 | m | V 2 | 3 | kT . | ||
2 | 2 | ||||||
2 | |||||||
Откуда следует, что:
1.Температура есть мера средней энергии хаотического движения;
2.Средняя энергия хаотического (теплового) движения молекул ~kT.
Заметим, что
V 2 V 2 | V 2 | V 2 | и V 2 | V 2 | V 2 |
x | y | z | x | y | z |
из-за хаотичности теплового движения, поэтому
mV 2 | mVy2 | mV 2 | 1 | ||
x | z | kT . | |||
2 | 2 | 2 | |||
2 | |||||
Полученный результат является частным случаем более общей теоремы о равномерном распределении энер-
гии по степеням свободы: на каждую степень свободы
молекулы приходится в среднем одинаковая кинетиче-
ская энергия теплового движения, равная 12 kT .
Согласно теореме о равномерном распределении энергии по степеням свободы полная энергия теплового движения молекулы:
E 2i kT .
Вычислим внутреннюю энергию идеального газа:
U | m | N A E | m | R | i | T , |
M | M | |||||
2 | ||||||
где NA – число Авогадро (число молекул в моле газа),

99
С | dU | i | R . | ||||||||||||
V | dT | 2 | |||||||||||||
Из приведённого выражения видно, | что теплоем- | ||||||||||||||
СV | кость | не должна | зависеть от | ||||||||||||
7 | 2 R | температуры. Однако опыт по- | |||||||||||||
5 | 2 R | казывает, что это не так. При- | |||||||||||||
мерная зависимость СV двух- | |||||||||||||||
3 2 R | H2 | атомного газа от | температуры | ||||||||||||
представлена на рисунке 21. | |||||||||||||||
Рис. 21 | T | Из графика следует, что | |||||||||||||
не все степени свободы прояв- | |||||||||||||||
ляются одновременно. При низких температурах исчезают (вымораживаются) вращательные степени свободы, при высоких температурах появляется колебательная степень свободы.
Этот экспериментальный результат может быть объяснен только с позиций квантовой теории.
12.2. Молекулярно-кинетическая | теория позволяет | ||||
получить уравнение | состояния | ||||
идеального газа. Полагаем, | что | ||||
p | |||||
молекулы идеального | газа при | ||||
ударах друг с другом и со стен- | |||||
m V | ками сосуда | ведут | себя | как | |
упругие шары (рис. 22). При | |||||
x | |||||
ударе молекулы идеального газа | |||||
о стенку, она передает стенке | |||||
импульс p 2mV cos 2mVx | |||||
Рис. 22 Задачу расчета давления можно упростить, предпо-
ложив, что молекулы движутся только вдоль координатных осей. Будем считать, что в направлении каждой из осей в среднем движется 1/6 часть всех молекул (с учетом
Источник
1. На рисунке схематически изображен цикл Карно в координатах :
Уменьшение энтропии имеет место на участке …
| 3-4 |
| 1-2 |
| 2-3 |
| 4-1 |
Решение:
Цикл Карно состоит из двух изотерм и двух адиабат (изотермического расширения 1-2, адиабатного расширения 2-3, изотермического сжатия 3-4 и адиабатного сжатия 4-1). Энтропия определяется соотношением , где – количество теплоты, сообщаемое системе. В адиабатном процессе энтропия не изменяется, так как адиабатный процесс протекает без теплообмена с окружающей средой. Для изотермического процесса согласно первому началу термодинамики . При сжатии работа газа отрицательна. Следовательно, при изотермическом сжатии рабочее тело отдает теплоту. Поэтому при изотермическом сжатии , то есть уменьшение энтропии имеет место на участке 3-4.
2. На рисунке схематически изображен цикл Карно в координатах :
Увеличение энтропии имеет место на участке …
| 1-2 |
| 2-3 |
| 3-4 |
| 4-1 |
Решение:
Цикл Карно состоит из двух изотерм и двух адиабат (изотермического расширения 1-2, адиабатного расширения 2-3, изотермического сжатия 3-4 и адиабатного сжатия 4-1). Энтропия определяется соотношением , где – количество теплоты, сообщаемое системе. В адиабатном процессе энтропия не изменяется, так как адиабатный процесс протекает без теплообмена с окружающей средой. Для изотермического процесса, согласно первому началу термодинамики, . При расширении работа газа положительна. Следовательно, изотермическое расширение происходит за счет теплоты, получаемой рабочим телом. Поэтому при изотермическом расширении , то есть увеличение энтропии имеет место на участке .
3. В процессе кристаллизации вещества энтропия неизолированной термодинамической системы …
| убывает |
| остается постоянной |
| увеличивается |
| может как увеличиваться, так и оставаться постоянной |
Решение:
Отношение в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией системы: . Образование кристаллической решетки при кристаллизации вещества приводит к уменьшению энтропии: .
4. Если КПД цикла Карно равен 60%, то температура нагревателя больше температуры холодильника в ______ раз(а).
| 2,5 |
| 1,7 |
Решение:
КПД обратимого цикла Карно равен: , или ; следовательно, ; отсюда и
5.Если количество теплоты, отданное рабочим телом холодильнику, уменьшится в 2 раза, то коэффициент полезного действия тепловой машины …
Решение:
Коэффициент полезного действия тепловой машины определяется по формуле , где – количество теплоты, полученное рабочим телом от нагревателя; – количество теплоты, отданное рабочим телом холодильнику. При уменьшении в два раза коэффициент полезного действия . Найдем изменение . Коэффициент полезного действия тепловой машины увеличится на .
6. При поступлении в неизолированную термодинамическую систему тепла в ходе обратимого процесса для приращения энтропии верным будет соотношение …
Решение:
Отношение в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией системы: . В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах: . Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса: .

7. Максимальное значение КПД, которое может иметь тепловой двигатель с температурой нагревателя 327°С и температурой холодильника 27°С, составляет ____ %.
Решение:
КПД реального теплового двигателя всегда меньше КПД идеального (обратимого) теплового двигателя, работающего в тех же условиях, то есть при одних и тех же температурах нагревателя и холодильника. Коэффициент полезного действия идеального теплового двигателя определяется только температурами нагревателя и холодильника: . Таким образом, максимальное значение КПД, которое может иметь рассматриваемый тепловой двигатель, равно
8. На рисунке изображен цикл Карно в координатах , где S – энтропия. Адиабатное расширение происходит на этапе …
| 2-3 |
| 4-1 |
| 1-2 |
| 3-4 |
Решение:
Адиабатным называется процесс, протекающий без теплообмена с окружающей средой. Следовательно, для такого процесса Изменение энтропии определяется как , следовательно, в адиабатном процессе энтропия остается постоянной. Согласно первому началу термодинамики, для адиабатного процесса . При адиабатном расширении газ совершает работу над внешними телами ( ), следовательно, внутренняя энергия уменьшается ( ). Это означает, что температура газа понижается.
Таким образом, адиабатное расширение происходит на этапе 2-3.
9. На рисунке изображен цикл Карно в координатах (T, S), где S – энтропия. Изотермическое расширение происходит на этапе …
| 1 – 2 |
| 4 – 1 |
| 2 – 3 |
| 3 – 4 |
Решение:
Изотермические процессы происходят при постоянной температуре. При расширении газа будет увеличиваться энтропия. Изменение энтропии определяется как . Изотермическое расширение происходит на этапе 1- 2.
10. Процесс, изображенный на рисунке в координатах (T,S), где S-энтропия, является…
изохорным охлаждением изобарным сжатием
изотермическим сжатием адиабатным расширением
Решение:
11. В идеальной тепловой машине из каждого теплоты, получаемого от нагревателя, отдается холодильнику. Если температура холодильника 27°С, то температура нагревателя (в °С) равна …
Решение:
Коэффициент полезного действия тепловой машины определяется соотношением , где и – количество теплоты, полученное от нагревателя и отданное холодильнику соответственно. Для идеальной тепловой машины ( и – температура нагревателя и холодильника соответственно). Приравнивая правые части этих выражений, получаем . Отсюда .
12.В процессе изохорического охлаждения постоянной массы идеального газа его энтропия …
уменьшается не меняется увеличивается
Решение:
13.В процессе изотермического сообщения тепла постоянной массе идеального газа его энтропия …
не меняется уменьшается увеличивается
Решение:
14.В процессе обратимого адиабатического охлаждения постоянной массы идеального газа его энтропия …
уменьшается не меняется увеличивается
Решение:
15.При адиабатическом расширении идеального газа …
температура и энтропия не изменяются
температура и энтропия возрастают
температура понижается, энтропия не изменяется
температура понижается, энтропия возрастает
Решение:
16.Изменение внутренней энергии газа произошло только за счет работы сжатия газа в …
изотермическом процессе
изобарном процессе
изохорном процессе
адиабатическом процессе
Решение:
Источник