На рисунке представлен цикл тепловой машины в координатах
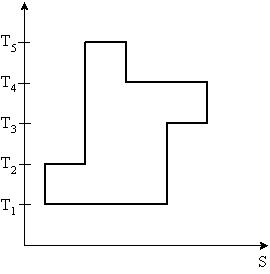
2.3.4-2
На рисунке представлен цикл тепловой машины в координатах T, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами.
| 1:Нагреватели – T3,T4,T5 Холодильники – T1,T2* 2:Нагреватели – T4,T5 Холодильники – T1,T2,T3 3:Нагреватели – T2,T3,T5 Холодильники – T1,T4 4:Нагреватели – T3,T5 Холодильники – T1,T2,T4 |
Будем считать, что цикл осуществляется в направлении, указанном на рисунке стрелками. Теплообмен происходит при изотермическом процессе (T-const). .
Q>0 (подводится тепло – нагреватель),S – возрастает, Q<0 (отводится тепло – холодильник), S – убывает. Таким образом, Q>0 при T3,T4,T5; Q<0 при T1,T2
Ответ: 1
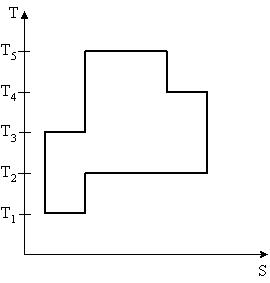
2.3.4-3
На рисунке представлен цикл тепловой машины в координатах T, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами.
| 1:Нагреватели – T2,T4,T5 Холодильники – T1,T3* 2:Нагреватели – T4,T5 Холодильники – T1,T2,T3 3:Нагреватели – T3,T4,T5 Холодильники – T1,T2 4:Нагреватели – T2,T4 Холодильники – T1,T3,T5 |
Будем считать, что цикл осуществляется в направлении, указанном на рисунке стрелками. Теплообмен происходит при изотермическом процессе (T-const). . Q>0(подводится тепло – нагреватель),S – возрастает, Q<0(отводится тепло – холодильник), S – убывает. Таким образом, Q>0 при T2,T4,T5; Q<0 при T1,T3
Ответ: 1
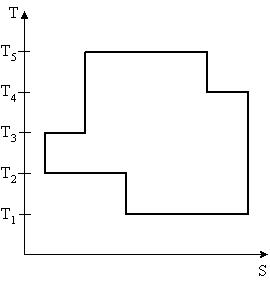
2.3.4-4
На рисунке представлен цикл тепловой машины в координатах T, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами.
| 1:Нагреватели – T3,T4,T5 Холодильники – T1,T2* 2:Нагреватели – T4,T5 Холодильники – T1,T2,T3 3:Нагреватели – T3,T5 Холодильники – T1,T2,T4 4:Нагреватели – T2,T4,T5 Холодильники – T1,T3 |
Будем считать, что цикл осуществляется в направлении, указанном на рисунке стрелками. Теплообмен происходит при изотермическом процессе (T-const). . Q>0(подводится тепло – нагреватель),S – возрастает, Q<0(отводится тепло – холодильник), S – убывает. Таким образом, Q>0 при T3,T4,T5; Q<0 при T1,T2.
Ответ: 1
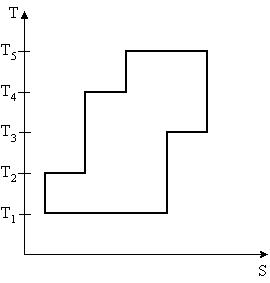
2.3.4-5
На рисунке представлен цикл тепловой машины в координатах T, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами.
| 1:Нагреватели – T2,T4,T5 Холодильники – T1,T3* 2:Нагреватели – T4,T5 Холодильники – T1,T2,T3 3:Нагреватели – T2,T5 Холодильники – T1,T3,T4 4:Нагреватели – T3,T4,T5 Холодильники – T1,T2 |
Б удем считать, что цикл осуществляется в направлении, указанном на рисунке стрелками. Теплообмен происходит при изотермическом процессе (T-const). . Q>0 (подводится тепло – нагреватель),S – возрастает, Q<0 (отводится тепло – холодильник), S – убывает. Таким образом, Q>0 при T2,T4,T5; Q<0 при T1,T3.
Ответ: 1
2.3.5-1
Газ находится в состоянии с параметрами P1,V1. Необходимо расширить газ, затратив при этом минимум энергии. Для этого подходит процесс … | 1. изотермический* 2. изобарический 3. ни один процесс не подходит 4. изохорический 5. адиабатический* |
Изотермический, т.к. при этом процессе =0, а Q=A, следовательно, затрачивается минимум энергии. Или адиабатический, т.к. расширение происходит за счет внутренней энергии.
Ответ: 1 или 5
2.3.6-1
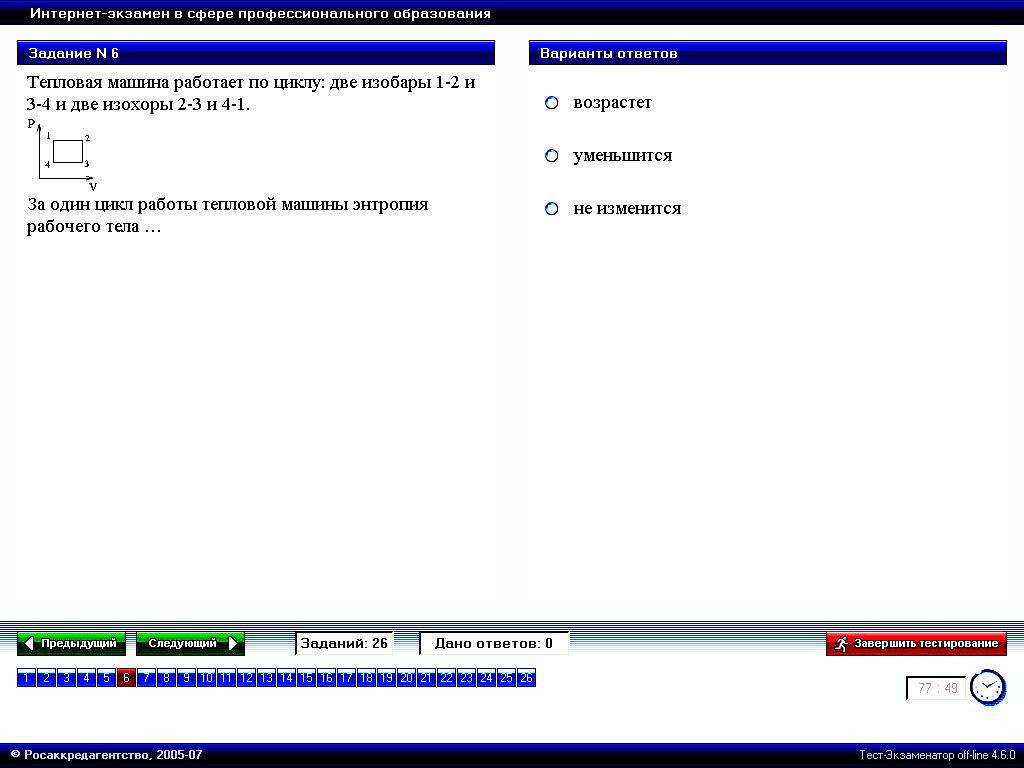
Тепловая машина работает по циклу: две изобары 1-2 и 3-4 и две изохоры 2-3 и 4-1.
За один цикл работы тепловой машины энтропия рабочего тела … | 1. возрастёт 2. уменьшится 3. не изменится* |
Энтропия является функцией состояния и за цикл начальное и конечное состояния совпадают, поэтому изменение энтропии равно нулю.
2.3.7-1
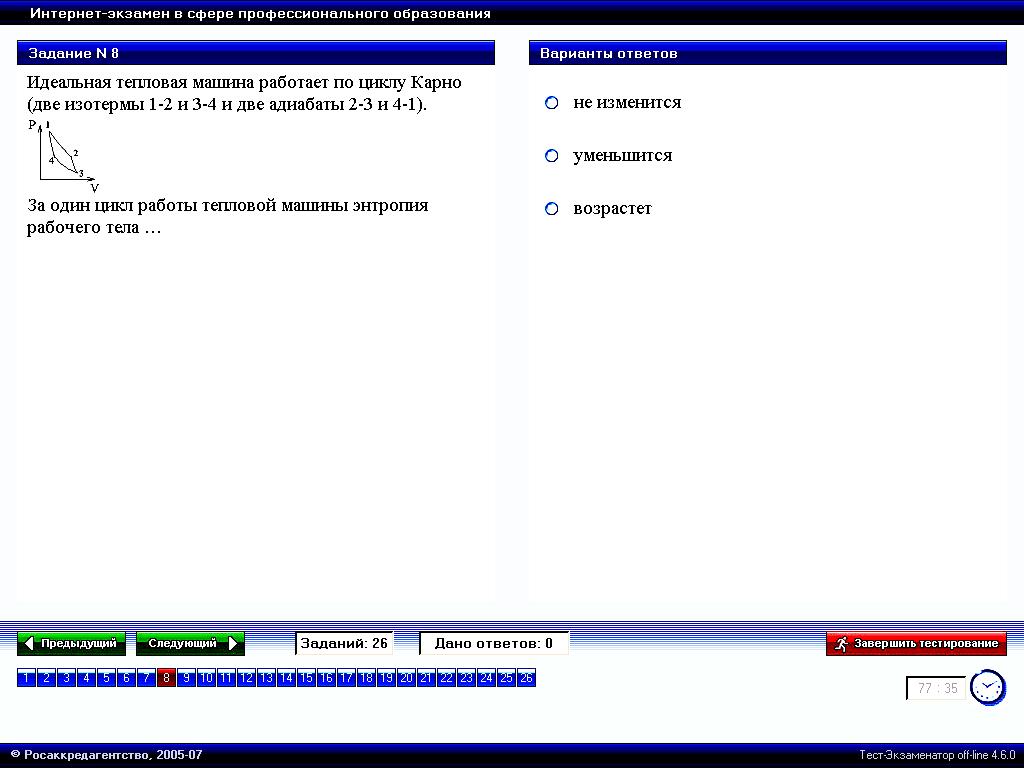
Идеальная тепловая машина работает по циклу Карно (две изотермы 1-2 и 3-4 и две адиабаты 2-3 и 4-1).
За один цикл работы тепловой машины энтропия рабочего тела … | 1. не изменится* 2. уменьшится 3. возрастёт |
Энтропия является функцией состояния и за цикл начальное и конечное состояния совпадают, поэтому изменение энтропии равно нулю.
2.3.8-1
Тепловая машина работает по циклу Карно. Если температуру нагревателя увеличить, то КПД цикла… | 1: увеличится* 2: не изменится 3: уменьшится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника. Если T1 – увеличится, то – уменьшится, и – увеличится. Следовательно, при увеличении температуры нагревателя КПД цикла также увеличится.
Ответ: 1
2.3.8-2
Тепловая машина работает по циклу Карно. Если температуру нагревателя уменьшить, то КПД цикла… | 1: уменьшится* 2: увеличится 3: не изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника. Если T1 – уменьшится, то – увеличится, и – уменьшится. Следовательно, при уменьшении температуры нагревателя КПД цикла также уменьшится.
Ответ: 1
2.3.8-3
Тепловая машина работает по циклу Карно. Если температуру холодильника увеличить, то КПД цикла… | 1: уменьшится* 2: увеличится 3: не изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника. Если T2 – увеличится, то – увеличится, и – уменьшится. Следовательно, при уменьшении температуры нагревателя КПД цикла также уменьшится.
Ответ: 1
2.3.8-4
Тепловая машина работает по циклу Карно. Если температуру холодильника уменьшить, то КПД цикла… | 1: увеличится* 2: уменьшится 3: е изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника. Если T2 – уменьшится, то – уменьшится, и – увеличится. Следовательно, при уменьшении температуры нагревателя КПД цикла также увеличится.
Ответ: 1
2.3.8-5
Тепловая машина работает по циклу Карно. Если температуру нагревателя и холодильника увеличить на одинаковую величину ΔT, то КПД цикла… | 1: уменьшится* 2: увеличится 3: не изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника
Значит, если температуру нагревателя и холодильника увеличить на одинаковую величину ΔT, т.е. и , , . Следовательно, при увеличении температуры нагревателя и холодильника на одинаковую величину ΔT, КПД цикла уменьшится.
2.3.8-6
Тепловая машина работает по циклу Карно. Если температуру нагревателя и холодильника уменьшить на одинаковую величину ΔT, то КПД цикла… | 1: увеличится* 2: уменьшится 3: не изменится |
В цикле Карно КПД считается по формуле: , где – температура нагревателя, – температура холодильника.
Значит, если температуру нагревателя и холодильника уменьшить на одинаковую величину ΔT, т.е. и , , . Следовательно, при уменьшении температуры нагревателя и холодильника на одинаковую величину ΔT, КПД цикла увеличится.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.
Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0):
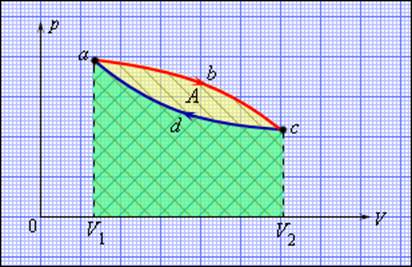
Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу A1, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A = A1 + A2 на диаграмме (p, V) равна площади цикла. Работа A положительна, если цикл обходится по часовой стрелке, и A отрицательна, если цикл обходится в противоположном направлении.
|
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd |
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно
При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (ΔU = 0). Согласно первому закону термодинамики,
Отсюда следует:
Работа A, совершаемая рабочим телом за цикл, равна полученному за цикл количеству теплоты Q. Отношение работы A к количеству теплоты Q1, полученному рабочим телом за цикл от нагревателя, называется коэффициентом полезного действия η тепловой машины:
 |
Модель. Термодинамические циклы. |
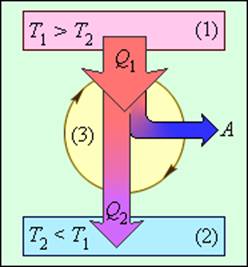
Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1). Энергетическая схема тепловой машины изображена на рис. 3.11.2.
|
Рисунок 3.11.2. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1 > 0, A > 0, Q2 < 0; T1 > T2 |
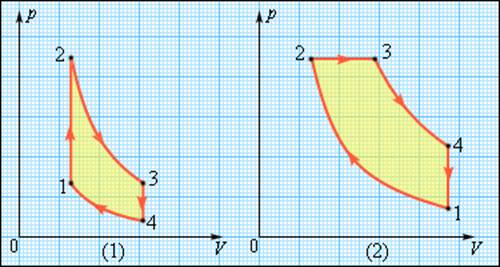
В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1-2, 3-4) и двух адиабат (2-3, 4-1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1-2, 3-4), одной изобары (2-3) и одной изохоры (4-1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.
|
Рисунок 3.11.3. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2) |
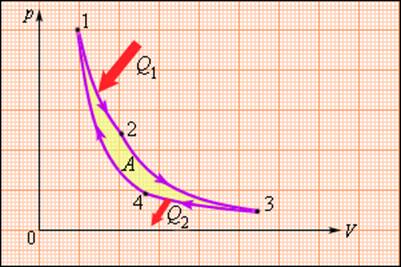
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).
|
Рисунок 3.11.4. Цикл Карно |
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1-2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2-3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3-4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:
A = A12 + A23 + A34 + A41.
На диаграмме (p, V) эта работа равна площади цикла.
Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1-2 и 3-4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).
Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для 1 моля газа
где T1 и T2 – начальная и конечная температуры газа.
Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам
По определению, коэффициент полезного действия η цикла Карно есть
С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T1 и холодильника T2:
Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с окружающими телами (тепловыми резервуарами или термостатами). Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника:
 |
Модель. Цикл Карно. |
Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине, когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной.
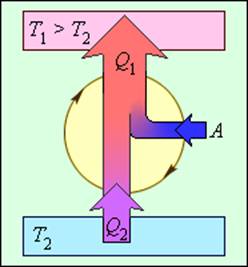
В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме (p, V) обходятся против часовой стрелки. Энергетическая схема холодильной машины представлена на рис. 3.11.5.
|
Рисунок 3.11.5. Энергетическая схема холодильной машины. Q1 < 0, A < 0, Q2 > 0, T1 > T2 |
Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q2| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением
т. е. эффективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении βх может быть и больше, и меньше единицы. Для обращенного цикла Карно
Если полезным эффектом является передача некоторого количества тепла |Q1| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность βТ теплового насоса может быть определена как отношение
т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
следовательно, βТ всегда больше единицы. Для обращенного цикла Карно
Источник
Молекулярно-кинетическая теория
Задание №12 в ЕГЭ по физике – последнее тестовое задание на тему термодинамики.
Теория к заданию №12 ЕГЭ по физике
КПД тепловой машины
Тепловая машина, или тепловой двигатель, представляет собой устройство, используемое для совершения механической работы механизмами (мотоциклами, автомобилями и др.). В самом общем виде это происходит так: в устройство подается топливо, внутренняя энергия которого преобразуется в механическую энергию. Работа при этом совершается за счет расширения газа (рабочего тела), возникающего при повышении его температуры при сгорании топлива. Повторяющийся круговой процесс такого плана, реализуемый в тепловых машинах, называют циклом Карно. Коэффициент полезного действия (КПД) – это величина, показывающая эффективность функционирования механизма. КПД обозначают греческой буквой ɳ («эта»). Вычисляется КПД так: где Т1 – температура нагревателя, Т2 – температура холодильника. Выражение Q1-Q2называют полезной работой, т.е. Q1-Q2=Ап. Поэтому КПД можно выразить формулой: где Q – кол-во теплоты, получаемой двигателем от нагревателя. КПД выражается в процентах или в долях. Формулы, которые необходимо применять для получения результата в долях, приведены выше. Для получения КПД в процентах следует использовать уравнения:
Адиабатный процесс
Адиабатный (адиабатический) процесс связан с первым термодинамическим законом. При нем изменение теплоты в системе равно сумме изменений тепловой энергии и выполненной работы, которую выполняет газ. Он протекает без передачи газу теплоты. Не происходит и передача теплоты газом внешней среде. Адиабатический процесс графически изображается так:
Разбор типовых вариантов № 12 ЕГЭ по физике
Демонстрационный вариант 2018
Тепловая машина работает по циклу Карно. Температуру холодильника тепловой машины повысили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
- увеличилась,
- уменьшилась,
- не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Работа газа за цикл |
Алгоритм решения:
- Записываем формулу расчета КПД. Анализируем, что произойдет, если температуру нагревателя увеличить.
- Записываем формулу для КПД, выраженного через работу. Анализируем, как изменится эта величина.
- Записываем ответ.
Решение:
1. Для любого двигателя показатель КПД определяется формулой:
,
где Тн – температурный показатель нагревателя, Тх – температурный показатель холодильника. Т.к. величина Тх в формуле присутствует со знаком «-», значит, повышение значения этой величины ведет к уменьшению результата (т.е. ɳ). Вывод: увеличение температурного показателя холодильника приведет к уменьшению полезного коэффициента. Правильный вариант ответа – 2.
2. КПД выражается через работу так: ɳ=????/????н. Отсюда А= ηQн. Из формулы видно, что ɳ пропорционально А. Вывод: если уменьшится КПД, работа тоже уменьшится. Прав.вариант ответа – 2.
3. Заполняем таблицу:
| КПД тепловой машины | Работа газа за цикл |
| 2 | 2 |
Ответ: 22
Первый вариант задания (Демидова, №3)
На рисунках приведены графики А и Б двух процессов, 1-2 и 3-4, происходящих с 1 моль гелия. Графики построены в координатах V-T и p-V, где р – давление, V – объём, Т – абсолютная температура газа. Установите соответствие между графиками и утверждениями, характеризующими изображённые на графиках процессы. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ | УТВЕРЖДЕНИЯ 1) Над газом совершают работу, при этом его внутренняя энергия увеличивается. 2) Над газом совершают работу, при этом газ отдаёт положительное количество теплоты. 3) Газ получает положительное количество теплоты и совершает работу. 4) Газ получает положительное количество теплоты, при этом его внутренняя энергия увеличивается. |
Алгоритм решения:
- Рассматриваем первый график таблицы. Ищем правильное предложение в графе справа.
- Проводим анализ второго графика в левой графе таблицы. Определяем правильный ответ в графе справа.
- Записываем ответ.
Решение:
1. На графике А) температура повышается, но объем не изменяется. Это изохорный процесс, поэтому газ не совершает работы, и над газом работа не совершается. Поскольку темп-ра увеличивается (происходит нагревание), газ получает некоторое кол-во теплоты. Из 1-го з-на термодинамики (Q=∆U+A) следует, что его внутр.энергия возрастает. Анализируем утверждения: 1) Утверждение 1 неверно в своей первой части; 2) Утверждение 2 неверно полностью; 3) Утверждение 3 неверно в своей 2-й части; 4) Утверждение 4 верно.
2. Вариант Б) показывает: уменьшаются показатели объема газа и давления. Происходит сжатие газа; это означает, что над газом производится работа. Применив ур-ние Менделеева-Клапейрона (pV=νRT), делаем вывод: при снижении объема и давления должна снижаться и температура. А из этого утверждения в свою очередь следует, что снижается внутр.энергия газа. Кол-во теплоты (положительное) при этом отдается. Работа над газом в данном случае совершается. Анализируем утверждения: 1) Утверждение 1 неверно во 2-й своей части; 2) Утверждение 2 верно; 3) Утверждения 3 и 4 неверны полностью.
Ответ: 42
Второй вариант задания (Демидова, №20)
Установите соответствие между процессами в идеальном газе и формулами, которыми они описываются (N – число частиц, р – давление, V – объём, Т – абсолютная температура, Q – количество теплоты.) К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫА) изохорный процесс при N = const Б) адиабатный процесс при N = const | ФОРМУЛЫ |
Алгоритм решения:
- Анализируем, что происходит при изохорном типе процесса. Определяем, какой вариант равенств соответствует такому процессу.
- Анализируем, каким образом происходит адиабатический процесс. Устанавливаем, какое равенство соответствует данному процессу.
- Записываем ответ.
Решение:
1. Справа вариантом А) записано, что происходит изохорный процесс. Он совершается при постоянном показателе объема. В этом случае действует з-н Шарля: р/Т= const. Такое равенство стоит под 1-м номером.
2. При адиабатическом процессе Б) не происходит теплового обмена со средой, то есть выполняется равенство: Q=0. Значит, правильные предложения 1 и 4.
Ответ: 14
Даниил Романович | ???? Скачать PDF | Просмотров: 4.4k | Оценить:
Источник