Матлаб цикл по времени

| Подборка по базе: Надякина Дарья Николаевна англ.язык 09.06.2020.docx, пакет NNT MATLAB.docx, резюме англ.docx, тема англ.docx, Проект англ..docx, КТ Англ.яз (Приложение 6).docx, кр.Байбородина 241908 англ.яз.в проф.docx, 2 сем. Англ.яз.docx, Письменная работа англ.docx, Звуки англ..doc 5.2. Оператор цикла while Язык программирования MatLab имеет два оператора цикла: while и for. С их помощью, например, выполняется программирование рекуррентных алгоритмов, подсчета суммы ряда, перебора элементов массива и многое другое. В самом простом случае цикл в программе организуется с помощью оператора while, который имеет следующий синтаксис: while end Здесь означает условное выражение подобное тому, которое применяется в операторе if, и цикл while работает до тех пор, пока это условие истинно. Следует обратить внимание на то, что если условие будет ложным до начала выполнения цикла, то операторы, входящие в цикл, не будут выполнены ни разу. Приведем пример работы цикла while для подсчета суммы ряда : S = 0; % начальное значение суммы i=1; % счетчик суммы while i S=S+i; % подсчитывается сумма i=i+1; % увеличивается счетчик на 1 end % конец цикла disp(S); % отображение суммы 210 на экране Теперь усложним задачу и будем подсчитывать сумму ряда , пока . Здесь в операторе цикла получается два условия: либо счетчик по i доходит до 20, либо значение суммы S превысит 20. Данную логику можно реализовать с помощью составного условного выражения в операторе цикла while: S = 0; % начальное значение суммы i=1; % счетчик суммы while i S=S+i; % подсчитывается сумма i=i+1; % увеличивается счетчик на 1 end % конец цикла disp(S); % отображение суммы 21 на экране Приведенный пример показывает возможность использования составных условий в цикле while. В общем случае в качестве условного выражения можно записывать такие же условия, что и в условном операторе if. Работу любого оператора цикла, в том числе и while, можно принудительно завершить с помощью оператора break. Например, предыдущую программу можно переписать следующим образом с использованием оператора break: S = 0; % начальное значение суммы i=1; % счетчик суммы while i S=S+i; % подсчитывается сумма i=i+1; % увеличивается счетчик на 1 if S > 20 % если S > 20, break; % то цикл завершается end end % конец цикла disp(S); % отображение суммы 21 на экране В данном примере второе условие завершения цикла, когда S будет больше 20, записано в самом цикле и с помощью оператора break осуществляется выход из цикла на функцию disp(), стоящую сразу после цикла while. Второй оператор управления выполнением цикла continue позволяет пропускать выполнение фрагмента программы, стоящий после него. Например, требуется подсчитать сумму элементов массива a = [1 2 3 4 5 6 7 8 9]; исключая элемент с индексом 5. Такую программу можно записать следующим образом: S = 0; % начальное значение суммы a = [1 2 3 4 5 6 7 8 9]; % массив i=0; % счетчик индексов массива while i % длины массива а) i=i+1; % увеличивается счетчик индексов на 1 if i == 5 % если индекс равен 5 continue; % то его не подсчитываем end S=S+a(i); % подсчитывается сумма элементов end % конец цикла disp(S); % отображение суммы 40 на экране Следует отметить, что в данной программе увеличение индекса массива i происходит до проверки условия. Это сделано для того, чтобы значение индекса увеличивалось на 1 на каждой итерации работы цикла. Если увеличение счетчика i записать как в предыдущих примерах, т.е. после подсчета суммы, то из-за оператора continue его значение остановилось бы на 5 и цикл while работал бы «вечно». 5.3. Оператор цикла forЧасто при организации цикла требуется перебирать значение счетчика в заданном диапазоне значений и с заданным шагом изменения. Например, чтобы перебрать элементы вектора (массива), нужно организовать счетчик от 1 до N с шагом 1, где N – число элементов вектора. Чтобы вычислить сумму ряда, также задается счетчик от a до b с требуемым шагом изменения step. И так далее. В связи с тем, что подобные задачи часто встречаются в практике программирования, для их реализации был предложен свой оператор цикла for, который позволяет проще и нагляднее реализовывать цикл со счетчиком. Синтаксис оператора цикла for имеет следующий вид: for = :: end Рассмотрим работу данного цикла на примере реализации алгоритма поиска максимального значения элемента в векторе: a = [3 6 5 3 6 9 5 3 1 0]; m = a(1); % текущее максимальное значение for i=1:length(a) % цикл от 1 до конца вектора с % шагом 1 (по умолчанию) if m m, m = a(i); % то m = a(i) end end % конец цикла for disp(m); В данном примере цикл for задает счетчик i и меняет его значение от 1 до 10 с шагом 1. Обратите внимание, что если величина шага не указывается явно, то он берется по умолчанию равным 1. В следующем примере рассмотрим реализацию алгоритма смещения элементов вектора вправо, т.е. предпоследний элемент ставится на место последнего, следующий – на место предпоследнего, и т.д. до первого элемента: a = [3 6 5 3 6 9 5 3 1 0]; disp(a); for i=length(a):-1:2 % цикл от 10 до 2 с шагом -1 a(i)=a(i-1); % смещаем элементы вектора а end % конец цикла for disp(a); Результат работы программы 3 6 5 3 6 9 5 3 1 0 3 3 6 5 3 6 9 5 3 1 Приведенный пример показывает, что для реализации цикла со счетчиком от большего значения к меньшему, нужно явно указывать шаг, в данном случае, -1. Если этого не сделать, то цикл сразу завершит свою работу и программа будет работать некорректно. 6. Решения уравнения6.1. Графический метод решения уравненийВывод на экран сразу нескольких графиков предоставляет простейший способ найти приблизительное значение решения. На данном графике представлены графики функций y=sin(t)/t и (x/5)2+y2=1. Как не трудно заметить данные функции имеют три точки пересечения. 6.2. Поиск решения уравненияГрафическим методом можно лишь примерно оценить решение. Для более точного нахождения решения в пакете MatLAB необходимо воспользоваться функцией fsolve(уравнение, начальное значение). Позже мы познакомимся как с помощью данной функции решать системы уравнений. В простейшем случае решаемое уравнение можно указать можно указать в одинарных кавычках, например: ‘x*x-abs(x)’. Но данная функция имеет три решения, представленных на рис. Решение, которое найдет в этом случае функция fsolve будет определяться начальным значением откуда она начнет итерационную процедуру поиска решения. Например: fsolve(‘x*x-abs(x)’,-2), ans = -1.0000; fsolve(‘x*x-abs(x)’,0.6), ans = 1.0000; fsolve(‘x*x-abs(x)’,0.4), ans = 7.9062e-008. Функция fsolve продолжает итерационную процедуру до тех пор пока она не найдет решение с заданной точностью. По этому в нашем примере мы и получили 7.9062e-008 а не 0. В случае более сложных функций их удобнее представить в виде M файла. Тогда в качестве первого параметра функции fsolve подставляется в одинарных кавычках имя этого файла. 7. М-файлы7.1. M-file Работа из командной строки MatLab затрудняется, если требуется вводить много команд и часто их изменять. Ведение дневника при помощи команды diary и сохранение рабочей среды незначительно облегчают работу. Самым удобным способом выполнения групп команд MatLab является использование М-файлов, в которых можно набирать команды, выполнять их все сразу или частями, сохранять в файле и использовать в дальнейшем. Для работы с М-файлами предназначен редактор М-файлов. С его помощью можно создавать собственные функции и вызывать их, в том числе и из командного окна. Раскройте меню File основного окна MatLab и в пункте New выберите подпункт M-file. Новый файл открывается в окне редактора M-файлов, которое изображено на рисунке.
М-файлы в MatLab бывают двух типов: файл-программы (Script M-Files), содержащие последовательность команд, и файл-функции, ( M-Files), в которых описываются функции, определяемые пользователем. 7.2. Файл-программаНаберите в редакторе команды, приводящие к построению двух графиков на одном графическом окне
Сохраните теперь файл с именем mydemo.m в подкаталоге work основного каталога MatLab, выбрав пункт Save as меню File редактора. Для запуска на выполнение всех команд, содержащихся в файле, следует выбрать пункт Run в меню Debug. На экране появится графическое окно Figure 1, содержащее графики функций. Очень удобной возможностью, предоставляемой редактором М-файлов, является выполнение части команд. Закройте графическое окно Figure 1. Выделите при помощи мыши, удерживая левую кнопку, или клавишами со стрелками при нажатой клавише Shift, первые четыре команды и выполните их из пункта Text. Обратите внимание, что в графическое окно вывелся только один график, соответствующий выполненным: командам. Запомните, что для выполнения части команд их следует выделить и нажать клавишу F9. Отдельные блоки М-файла можно снабжать комментариями, которые пропускаются при выполнении, но удобны при работе с М-файлом. Комментарии начинаются со знака процента и автоматически выделяются зеленым цветом, например:
Открытие существующего М-файла производится при помощи пункта Open меню File рабочей среды, либо редактора М-файлов. 7.3. Файл-функцияМ-функции являются M-файлами, которые допускают наличие входных и выходных аргументов. Они работают с переменными в пределах собственной рабочей области, отличной от рабочей области системы MATLAB. Пример_Функция_average_-_это_достаточно_простой_M-файл,_который_вычисляет_среднее_значение_элементов_вектора:__y_=_average_(x)’>Пример Функция average – это достаточно простой M-файл, который вычисляет среднее значение элементов вектора: y = average (x) % AVERAGE Среднее значение элементов вектора. % AVERAGE(X), где X – вектор. Вычисляет среднее значение элементов вектора. % Если входной аргумент не является вектором, генерируется ошибка. [m,n] = size(x); if ( ((m == 1) | (n == 1)) | (m == 1 & n == 1)) error(‘Входной массив должен быть вектором’) end y =sum(x)/length(x); % Собственно вычисление Попробуйте ввести эти команды в M-файл, именуемый average.m. Функция average допускает единственный входной и единственный выходной аргументы. Для того чтобы вызвать функцию average, надо ввести следующие операторы: z = 1:99; average(z) ans = 50 Структура М-функции. M-функция состоит из:
Строка определения функции. Строка определения функции сообщает системе MATLAB, что файл является М-функцией, а также определяет список входных аргументов. Пример Строка определения функции average имеет вид: y = average(x) Здесь:
Каждая функция в системе MATLAB содержит строку определения функции, подобную приведенной. Если функция имеет более одного выходного аргумента, список выходных аргументов помещается в квадратные скобки. Входные аргументы, если они присутствуют, помещаются в круглые скобки. Для отделения аргументов во входном и выходном списках применяются запятые. Пример [x, y, z] = sphere(theta, phi, rho) Имена входных переменных могут, но не обязаны совпадать с именами, указанными в строке определения функции. Первая строка комментария. Для функции average первая строка комментария выглядит так: % AVERAGE Среднее значение элементов вектора Это – первая строка текста, которая появляется, когда пользователь набирает команду help . Кроме того, первая строка комментария выводится на экран по команде поиска lookfor. Поскольку эта строка содержит важную информацию об M-файле, она должна быть тщательно составлена. Имена М-функций. В системе MATLAB на имена М-функций налагаются те же ограничения, что и на имена переменных – их длина не должна превышать 31 символа. Более точно, имя может быть и длиннее, но система MATLAB принимает во внимание только первые 31 символ. Имена М-функций должны начинаться с буквы; остальные символы могут быть любой комбинацией букв, цифр и подчеркиваний. Имя файла, содержащего М-функцию, составляется из имени функции и расширения “.m”. Пример average.m Если имя файла и имя функции в строке определения функции разные, то используется имя файла, а внутреннее имя игнорируется. Хотя имя функции, определенное в строке определения функции, может и не совпадать с именем файла, настоятельно рекомендуется использовать одинаковые имена. 1 2 3 4 5 6 |
Источник
 ОСНОВЫ ПРОГРАМИРОВАНИЯ В MATLAB 1
ОСНОВЫ ПРОГРАМИРОВАНИЯ В MATLAB 1
 Операторы цикла В MATLAB повторяющиеся действия осуществляются с помощью операторов циклов for и while. Самое простое использование for осуществляется следующим образом: 2
Операторы цикла В MATLAB повторяющиеся действия осуществляются с помощью операторов циклов for и while. Самое простое использование for осуществляется следующим образом: 2
 For count = start: step: final Команды MATLAB End Здесь count – переменная цикла; n start, final – начальное и конечное действительное значение; n step – шаг из множества действительных чисел (по умолчанию равен 1, его можно опустить). Цикл заканчивается, как становиться больше final. только count 3
For count = start: step: final Команды MATLAB End Здесь count – переменная цикла; n start, final – начальное и конечное действительное значение; n step – шаг из множества действительных чисел (по умолчанию равен 1, его можно опустить). Цикл заканчивается, как становиться больше final. только count 3
 Пример 1 Вычислить сумму при x= -1, 0, 1. Решение В редакторе M-file создадим файл-программу. Сохраняем её в файле Summa. m S = 0; for k = 1 : 10 S = S + x. ^ k / factorial(k); End S В командной строке x = -1: 1: 1; Summa S = -0. 6 0 1. 7 Заметим, что переменные k, s глобальные. 4
Пример 1 Вычислить сумму при x= -1, 0, 1. Решение В редакторе M-file создадим файл-программу. Сохраняем её в файле Summa. m S = 0; for k = 1 : 10 S = S + x. ^ k / factorial(k); End S В командной строке x = -1: 1: 1; Summa S = -0. 6 0 1. 7 Заметим, что переменные k, s глобальные. 4
 Удобнее для этого примера использовать файлфункцию. В редакторе М-файлов В командной строке создаем файл-функцию S = funsum(x, N) > f = funsum (-1 : 1, 10) S = 0; > f = for m = 1 : N -0. 6 0 1. 7 S = S + x. ^ m / factorial(m); end Здесь переменные s, m локальные. 5
Удобнее для этого примера использовать файлфункцию. В редакторе М-файлов В командной строке создаем файл-функцию S = funsum(x, N) > f = funsum (-1 : 1, 10) S = 0; > f = for m = 1 : N -0. 6 0 1. 7 S = S + x. ^ m / factorial(m); end Здесь переменные s, m локальные. 5
 Пример 2 Создать матрицу Гильберта порядка n. Решение n = 4; a = zeros (n, n); for i = 1 : n for j = 1: n a (i, j) = 1 / (i+j-1); end a 6
Пример 2 Создать матрицу Гильберта порядка n. Решение n = 4; a = zeros (n, n); for i = 1 : n for j = 1: n a (i, j) = 1 / (i+j-1); end a 6
 Замечание Перед заполнением матриц и векторов следует сначала создать их и заполнить нулями командой zeros, для увеличения скорости алгоритма (то есть a = zeros (n, n) быстрее, чем a(i, j) = 0, i, j = 1, …, n). 7
Замечание Перед заполнением матриц и векторов следует сначала создать их и заполнить нулями командой zeros, для увеличения скорости алгоритма (то есть a = zeros (n, n) быстрее, чем a(i, j) = 0, i, j = 1, …, n). 7
 Цикл for оказывается полезным, при выполнении повторяющихся действий, когда их число заранее известно. В случае, если их число заранее неизвестно можно воспользоваться циклом while: While условие цикла Команды MATLAB Еnd 8
Цикл for оказывается полезным, при выполнении повторяющихся действий, когда их число заранее известно. В случае, если их число заранее неизвестно можно воспользоваться циклом while: While условие цикла Команды MATLAB Еnd 8
 Пример 3 Найти сумму ряда для заданного x До бесконечности суммировать не удастся, но можно накапливать сумму, пока слагаемые не будут слишком маленькими, например, пока 9
Пример 3 Найти сумму ряда для заданного x До бесконечности суммировать не удастся, но можно накапливать сумму, пока слагаемые не будут слишком маленькими, например, пока 9
 Замечание Малость слагаемого – понятие относительное, слагаемое, может быть, скажем, порядка 10 -10, но и сама сумма того же порядка. В этом случае нельзя останавливать суммирование. Не будем пока обращать на это внимание и вернемся к решению. 10
Замечание Малость слагаемого – понятие относительное, слагаемое, может быть, скажем, порядка 10 -10, но и сама сумма того же порядка. В этом случае нельзя останавливать суммирование. Не будем пока обращать на это внимание и вернемся к решению. 10
 M-file функция В командной строке S = mysin(x) > f = mysin (1) S = 0; 0. 8415 k = 0; while abs(x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10 S = S + (-1)^k * x. ^ (2*k + 1)/factorial(2*k + 1); k = k + 1; end 11
M-file функция В командной строке S = mysin(x) > f = mysin (1) S = 0; 0. 8415 k = 0; while abs(x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10 S = S + (-1)^k * x. ^ (2*k + 1)/factorial(2*k + 1); k = k + 1; end 11
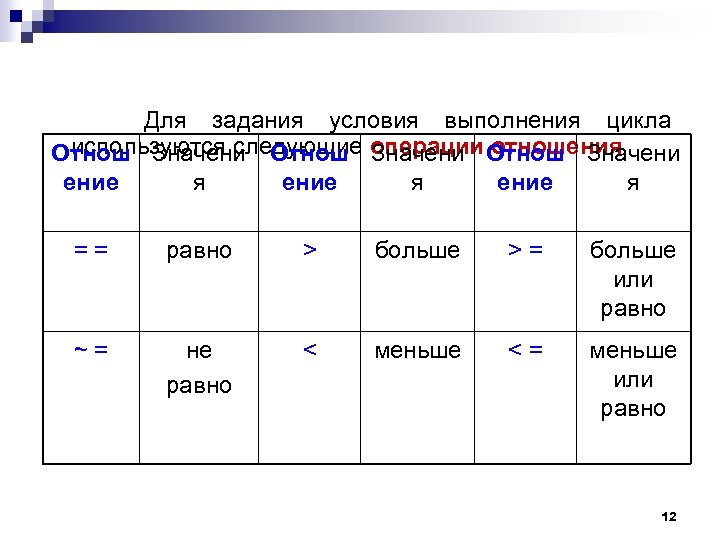 Для задания условия выполнения цикла используются следующие операции отношения Отнош Значени ение я = = равно > больше > = больше или равно ~ = не равно
Для задания условия выполнения цикла используются следующие операции отношения Отнош Значени ение я = = равно > больше > = больше или равно ~ = не равно
 и логические операторы: Оператор Условие Запись в MATLAB Эквивалентная запись Логическое «и» x
и логические операторы: Оператор Условие Запись в MATLAB Эквивалентная запись Логическое «и» x
 Вернемся к нашему примеру, и заметим, что если ряд расходится, то условие на малость текущего слагаемого может никогда не выполнится и программа зациклиться. Поэтому ограничим число слагаемых 100. 000 Условие будет выглядеть так or (abs (x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10, k
Вернемся к нашему примеру, и заметим, что если ряд расходится, то условие на малость текущего слагаемого может никогда не выполнится и программа зациклиться. Поэтому ограничим число слагаемых 100. 000 Условие будет выглядеть так or (abs (x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10, k
 Обработка исключительных ситуаций 1) break – прерывание цикла и выполнение оператора следующего за end (например, выход из внутреннего цикла); 2) Часть некорректных математических операций в MATLAB, не приводит к завершению работы программы (например, = inf, = Na. N). Выходом является конструкция try Операторы, выполнение которых может привести к ошибке catch Операторы в случае ошибки end 15
Обработка исключительных ситуаций 1) break – прерывание цикла и выполнение оператора следующего за end (например, выход из внутреннего цикла); 2) Часть некорректных математических операций в MATLAB, не приводит к завершению работы программы (например, = inf, = Na. N). Выходом является конструкция try Операторы, выполнение которых может привести к ошибке catch Операторы в случае ошибки end 15
 Операторы ветвления Условный оператор В MATLAB используются следующие операторы ветвления: n if – условный оператор; n switch – оператор переключения 16
Операторы ветвления Условный оператор В MATLAB используются следующие операторы ветвления: n if – условный оператор; n switch – оператор переключения 16
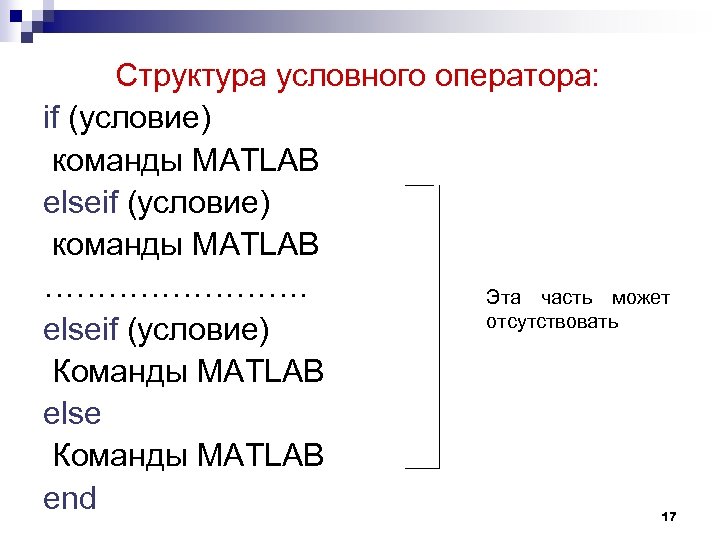 Структура условного оператора: if (условие) команды MATLAB elseif (условие) команды MATLAB …………. Эта часть может отсутствовать elseif (условие) Команды MATLAB else Команды MATLAB end 17
Структура условного оператора: if (условие) команды MATLAB elseif (условие) команды MATLAB …………. Эта часть может отсутствовать elseif (условие) Команды MATLAB else Команды MATLAB end 17
 При составлении М-файла, использующего операторы ветвления, полезно применять 1) команду warning (‘текст’) – для вывода предупреждения в командное окно; 2) функцию error (‘текст’) – для прекращения выполнения программы. 18
При составлении М-файла, использующего операторы ветвления, полезно применять 1) команду warning (‘текст’) – для вывода предупреждения в командное окно; 2) функцию error (‘текст’) – для прекращения выполнения программы. 18
 Пример 4 Дано квадратное уравнение ax 2 + bx +c = 0, a ≠ 0. Напишем М-функцию вычисляющую корни квадратного уравнения. Сделаем проверку на количество входных и выходных параметров, а так же на то, что входные параметры являются числами, а не векторами и матрицами. Более того, учтем случай комплексного корня. Программа выглядит так: 19
Пример 4 Дано квадратное уравнение ax 2 + bx +c = 0, a ≠ 0. Напишем М-функцию вычисляющую корни квадратного уравнения. Сделаем проверку на количество входных и выходных параметров, а так же на то, что входные параметры являются числами, а не векторами и матрицами. Более того, учтем случай комплексного корня. Программа выглядит так: 19
![[x 1, x 2] = root 2 (a, b, c) if (nargin <3)](https://present5.com/presentation/c993b082b44b0b84b1886b8dd4d3c841/image-20.jpg) [x 1, x 2] = root 2 (a, b, c) if (nargin
[x 1, x 2] = root 2 (a, b, c) if (nargin
 Замечание Для написания собственных вычислительных программ большую пользу может принести самостоятельное изучение стандартных файл-функций в подкаталогах Toolbox. Большинство из них имеют открытый код, что позволяет понять принципы программирования в MATLAB. Другие функции (например, cos. m) являются встроенными. Они содержат комментарии об использовании функций. Приведем еще один пример. 21
Замечание Для написания собственных вычислительных программ большую пользу может принести самостоятельное изучение стандартных файл-функций в подкаталогах Toolbox. Большинство из них имеют открытый код, что позволяет понять принципы программирования в MATLAB. Другие функции (например, cos. m) являются встроенными. Они содержат комментарии об использовании функций. Приведем еще один пример. 21
 Пример 5 Вычисление кусочно-заданной функции входным элементом, которой является матрица. Программа выглядит так: 22
Пример 5 Вычисление кусочно-заданной функции входным элементом, которой является матрица. Программа выглядит так: 22
 y = kusfun (x) If nargin ~= 1 error (‘Должен быть один входной аргумент’) end [Nx, Mx] = size(x); y = zeros (size(x)); % инициализирует входной аргумент for i = 1 : Nx for j = 1 : Mx if x (i, j) = -pi не нужна! y (i, j) = x (i, j) / pi; else y (i, j) = – cos(x (i, j)) end end 23
y = kusfun (x) If nargin ~= 1 error (‘Должен быть один входной аргумент’) end [Nx, Mx] = size(x); y = zeros (size(x)); % инициализирует входной аргумент for i = 1 : Nx for j = 1 : Mx if x (i, j) = -pi не нужна! y (i, j) = x (i, j) / pi; else y (i, j) = – cos(x (i, j)) end end 23
 Оператор switch удобно применять тогда, когда есть соответствие между дискретными значениями некоторой переменной и последующими действиями. 24
Оператор switch удобно применять тогда, когда есть соответствие между дискретными значениями некоторой переменной и последующими действиями. 24
 Структура оператора видна из следующего примера: switch a case -1 disp (‘a = -1’) case 0 disp (‘a = 0’) otherwise disp (‘a не равно -1, 0’) end 25
Структура оператора видна из следующего примера: switch a case -1 disp (‘a = -1’) case 0 disp (‘a = 0’) otherwise disp (‘a не равно -1, 0’) end 25
 Оператор switch хорошо подходит для решения поставленной задачи о выводе различных графиков исследуемой функции (каркасная поверхность (а=1), линии уровня (а=2) и т. д. ). 26
Оператор switch хорошо подходит для решения поставленной задачи о выводе различных графиков исследуемой функции (каркасная поверхность (а=1), линии уровня (а=2) и т. д. ). 26
 Логические выражения с массивами и числами Универсальным способом обработки матричных данных служат логические операции. Поскольку MATLAB представляет числа массивами 1 1, то естественно ожидать, что массивы могут входить в логические выражения. Сейчас мы рассмотрим расширение логических операций и операций отношения на случай массивов. 27
Логические выражения с массивами и числами Универсальным способом обработки матричных данных служат логические операции. Поскольку MATLAB представляет числа массивами 1 1, то естественно ожидать, что массивы могут входить в логические выражения. Сейчас мы рассмотрим расширение логических операций и операций отношения на случай массивов. 27
 Операции отношения Результат операции отношения в MATLAB может быть или логическая единица (‘истина’) или логический нуль (‘ложь’). Причем в отличие от многих языков программирования арифметические переменные могут использоваться в одном выражении с логическими. 28
Операции отношения Результат операции отношения в MATLAB может быть или логическая единица (‘истина’) или логический нуль (‘ложь’). Причем в отличие от многих языков программирования арифметические переменные могут использоваться в одном выражении с логическими. 28
 Пример 6 • > a = 1; b = 3; c = 1; > a + (b > c) ans = 2 > a + (b
Пример 6 • > a = 1; b = 3; c = 1; > a + (b > c) ans = 2 > a + (b
![• > A = [1 2; 3 4]; B = [1 3; 4](https://present5.com/presentation/c993b082b44b0b84b1886b8dd4d3c841/image-30.jpg) • > A = [1 2; 3 4]; B = [1 3; 4 5]; > C = A = = B C = 30
• > A = [1 2; 3 4]; B = [1 3; 4 5]; > C = A = = B C = 30
 Замечание Так же как и в поэлементных арифметических операциях, допустимо использовать числа в качестве одного из аргументов операции отношения. В этом случае происходит сравнение каждого элемента массива с числом, результатом является массив того же размера, что и исходный. 31
Замечание Так же как и в поэлементных арифметических операциях, допустимо использовать числа в качестве одного из аргументов операции отношения. В этом случае происходит сравнение каждого элемента массива с числом, результатом является массив того же размера, что и исходный. 31
 Логические операции Применение логических операций к массивам приводит к поэлементному их выполнению над элементами массивов. n А and B – дает единицу, если соответствующие элементы не равны нулю; n A or B – дает единицу, если хотя бы один элемент не равен нулю; 32
Логические операции Применение логических операций к массивам приводит к поэлементному их выполнению над элементами массивов. n А and B – дает единицу, если соответствующие элементы не равны нулю; n A or B – дает единицу, если хотя бы один элемент не равен нулю; 32
 not A – применяется к одному массиву, если элемент не равен нулю, то ставится нуль, иначе – единица; n all (v) – проверка наличия нулевых элементов в векторе, возвращает единицу, если нет нулевых элементов. Если v – матрица, то результат по столбцам; n any (v) – возвращает единицу, если во входном векторе есть хотя бы один ненулевой элемент. n 33
not A – применяется к одному массиву, если элемент не равен нулю, то ставится нуль, иначе – единица; n all (v) – проверка наличия нулевых элементов в векторе, возвращает единицу, если нет нулевых элементов. Если v – матрица, то результат по столбцам; n any (v) – возвращает единицу, если во входном векторе есть хотя бы один ненулевой элемент. n 33
 Приоритет операций 1. Отрицание; 2. Транспонирование, возведение в степень (в том числе поэлементное), знак плюс и минус перед числом; 3. Умножение и деление (в том числе поэлементное); 4. Сложение и вычитание; 5. Операции отношения; 6. Логическое ‘и’, логическое ‘или’. 34
Приоритет операций 1. Отрицание; 2. Транспонирование, возведение в степень (в том числе поэлементное), знак плюс и минус перед числом; 3. Умножение и деление (в том числе поэлементное); 4. Сложение и вычитание; 5. Операции отношения; 6. Логическое ‘и’, логическое ‘или’. 34
 Логическое индексирование Выделение части массива, элементы которого удовлетворяют определенному условию производится функцией find. 35
Логическое индексирование Выделение части массива, элементы которого удовлетворяют определенному условию производится функцией find. 35
![Пример 7 > a = [2 3 0 -1 0 3]; > u](https://present5.com/presentation/c993b082b44b0b84b1886b8dd4d3c841/image-36.jpg) Пример 7 > a = [2 3 0 -1 0 3]; > u = find ((a = -1)) 3 4 5 > anew = a(u) 0 -1 0 36
Пример 7 > a = [2 3 0 -1 0 3]; > u = find ((a = -1)) 3 4 5 > anew = a(u) 0 -1 0 36
 Пример 8 Заменить самостоятельно элементы квадратной матрицы 5 x 5 случайных чисел из интервала (0, 1), больших среднего значения всех элементов на 10%, на среднее значение. Решение > A = rand (5); > S = sum (sum A) / 25; > A(find (A > S* 1. 1)) = S В данном случае функция find выдает 2 вектора номера строк и номера столбцов. 37
Пример 8 Заменить самостоятельно элементы квадратной матрицы 5 x 5 случайных чисел из интервала (0, 1), больших среднего значения всех элементов на 10%, на среднее значение. Решение > A = rand (5); > S = sum (sum A) / 25; > A(find (A > S* 1. 1)) = S В данном случае функция find выдает 2 вектора номера строк и номера столбцов. 37
 Полиномы в MATLAB Полином p (х) =anxn+an-1 xn-1+. . . +a 0, an≠ 0 в MATLAB задается вектор-строй р=[an, an-1, . . . , a 0] , где ai – любые комплексные числа, an≠ 0. Заметим, что степень полинома вычисляется так: n=length(р)-1 (при n=0 получается const). 38
Полиномы в MATLAB Полином p (х) =anxn+an-1 xn-1+. . . +a 0, an≠ 0 в MATLAB задается вектор-строй р=[an, an-1, . . . , a 0] , где ai – любые комплексные числа, an≠ 0. Заметим, что степень полинома вычисляется так: n=length(р)-1 (при n=0 получается const). 38
 Основные команд для действий с полиномами таковы: n n n r=roots(р) – вектор-столбец, содержащий все корни полинома; p=poly(r) – построение полинома по корням, заданным в векторе-столбце r, причем, если r квадратная матрица, то р – характеристический многочлен; y=polyval(p, x) – поэлементное вычисление у значений полиному р на множестве х, где х может быть вектором или матрицей; 39
Основные команд для действий с полиномами таковы: n n n r=roots(р) – вектор-столбец, содержащий все корни полинома; p=poly(r) – построение полинома по корням, заданным в векторе-столбце r, причем, если r квадратная матрица, то р – характеристический многочлен; y=polyval(p, x) – поэлементное вычисление у значений полиному р на множестве х, где х может быть вектором или матрицей; 39
 n n n polyder(p) – вектор-строка, производная от p (дифференцирование полинома p); polyder(p, q) -производная от произведения полиномов p и q; [a, b]= polyder(p, q) – производная от частного полиномом p и q, где a и b являются числителем и знаменателем получившейся дроби; 40
n n n polyder(p) – вектор-строка, производная от p (дифференцирование полинома p); polyder(p, q) -производная от произведения полиномов p и q; [a, b]= polyder(p, q) – производная от частного полиномом p и q, где a и b являются числителем и знаменателем получившейся дроби; 40
 n n n p=polyfit(x, y, n) – приближение функции y(x) полиномом p n-й степени по методу, минимизирующему расстояние между графиком полинома и истиной кривой, усредненное по всей их длине; conv(p, q) – вектор-строка, произведение полиномов p и q; [w, r]=deconv(p, q) – деление p на q, причем w-частное, r-остаток и p=conv (q, w) +r; 41
n n n p=polyfit(x, y, n) – приближение функции y(x) полиномом p n-й степени по методу, минимизирующему расстояние между графиком полинома и истиной кривой, усредненное по всей их длине; conv(p, q) – вектор-строка, произведение полиномов p и q; [w, r]=deconv(p, q) – деление p на q, причем w-частное, r-остаток и p=conv (q, w) +r; 41
![n [r, p, k]=residue(a, b) – разложение рациональной функции на простые дроби над полем](https://present5.com/presentation/c993b082b44b0b84b1886b8dd4d3c841/image-42.jpg) n [r, p, k]=residue(a, b) – разложение рациональной функции на простые дроби над полем комплексных чисел с выделением целой части k(х) или где ri – вычеты (элементы r), pi – полюса (элементы p). Эта команда работает и в обратную строну [a, b] =residue(r, p, k) 42
n [r, p, k]=residue(a, b) – разложение рациональной функции на простые дроби над полем комплексных чисел с выделением целой части k(х) или где ri – вычеты (элементы r), pi – полюса (элементы p). Эта команда работает и в обратную строну [a, b] =residue(r, p, k) 42
 Замечание 1. Если в residue (a, b) полином b(х), а в roots(p) полином р(х) имеют кратные или близкие друг к другу корни, то результаты могут быть неверными, поскольку такая задача плохо обусловлена. Плохая обусловленность – это крайне сильная зависимость результата от коэффициентов (аналог устойчивости решения в дифференциальных уравнениях). 43
Замечание 1. Если в residue (a, b) полином b(х), а в roots(p) полином р(х) имеют кратные или близкие друг к другу корни, то результаты могут быть неверными, поскольку такая задача плохо обусловлена. Плохая обусловленность – это крайне сильная зависимость результата от коэффициентов (аналог устойчивости решения в дифференциальных уравнениях). 43
![2. При работе с полиномами возникают полиномы вида [0, . . . ], а](https://present5.com/presentation/c993b082b44b0b84b1886b8dd4d3c841/image-44.jpg) 2. При работе с полиномами возникают полиномы вида [0, . . . ], а MATLAB автоматически не проверяет an≠ 0, и возникают ошибки (нужно самим следить). 44
2. При работе с полиномами возникают полиномы вида [0, . . . ], а MATLAB автоматически не проверяет an≠ 0, и возникают ошибки (нужно самим следить). 44
Источник


