Кпд цикла из треугольника
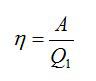
В термодинамике цикл Карно́ или процесс Карно́ – это идеальный[1]круговой процесс, состоящий из двух адиабатных и двух изотермических процессов[2]. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой – холодильником[3].
Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году[4][5].
Поскольку идеальные процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности.
Коэффициент полезного действия (КПД) любой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника[6]. По этой причине, позволяя оценить верхний предел КПД тепловой машины, цикл Карно важен для теории тепловых машин. В то же время КПД цикла Карно настолько чувствителен к отклонениям от идеальности (потерям на трение), что данный цикл никогда не применяли в реальных тепловых машинах[K 1][8].
Описание цикла Карно[править | править код]
Рис. 1. Цикл Карно в координатах T-S
Рис. 2. Цикл Карно в координатах p-V
Рис. 3. Цикл Карно на термодинамической поверхности идеального газа
Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две – при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах (температура) и (энтропия).
1. Изотермическое расширение (на рис. 1 – процесс A→B). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты , то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
2. Адиабатическое расширение (на рис. 1 – процесс B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника , тело совершает механическую работу, а энтропия остаётся постоянной.
3. Изотермическое сжатие (на рис. 1 – процесс C→D). Рабочее тело, имеющее температуру , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты . Над телом совершается работа, его энтропия уменьшается.
4. Адиабатическое сжатие (на рис. 1 – процесс D→A). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
Обратный цикл Карно[править | править код]
В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий[9][10]: адиабатического сжатия за счёт совершения работы (на рис. 1 – процесс C→B); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 – процесс B→A); адиабатического расширения (на рис. 1 – процесс A→D); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 – процесс D→C).
КПД тепловой машины Карно[править | править код]
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
Первая и вторая теоремы Карно[править | править код]
Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно[11]. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно[12][13]. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.
Связь между обратимостью цикла и КПД[править | править код]
Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.
Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД[14]. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например цикл Эрикссона (англ.)русск., состоящий из двух изобар и двух изотерм[14].
Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.
См. также[править | править код]
- Термодинамические циклы
- Первое начало термодинамики
- Второе начало термодинамики
- Термодинамическая энтропия
- Термодинамические потенциалы
Комментарии[править | править код]
- ↑ В реальных тепловых машинах цикл Карно не используют, поскольку практически невозможно осуществить процессы изотермического сжатия и расширения. Кроме того, полезная работа цикла, представляющая собой алгебраическую сумму работ во всех четырех составляющих цикл частных процессах, даже в идеальном случае полного отсутствия потерь мала по сравнению с работой в каждом из частных процессов, то есть мы имеем дело с обычной ситуацией, когда итоговый результат представляет собой малую разность больших величин. Применительно к математическим вычислениям это означает высокую отзывчивость результата даже на небольшие вариации значений исходных величин, а в рассматриваемом нами случае соответствует высокой чувствительности полезной работы цикла Карно и его КПД к отклонениям от идеальности (потерям на трение). Эта связь с отклонениями от идеальности настолько велика, что с учетом всех потерь полезная работа цикла Карно приближается к нулю[7].
Примечания[править | править код]
- ↑ То есть без потерь, в первую очередь на трение.
- ↑ Карно цикл // Италия – Кваркуш. – М. : Советская энциклопедия, 1973. – (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969-1978, т. 11).
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 94.
- ↑ Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. – Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. – 102 p. (фр.)
- ↑ Второе начало термодинамики. (Работы Сади Карно – В. Томсон – Кельвин – Р. Клаузиус – Л. Больцман – М. Смолуховский) / Под. ред. А. К. Тимирязева. – Москва-Ленинград: Государственное технико-теоретическое издательство, 1934. – С. 17-61.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113-114.
- ↑ Бэр Г. Д., Техническая термодинамика, 1977, с. 112.
- ↑ Кинан Дж., Термодинамика, 1963, с. 93.
- ↑ Николаев Г. П., Лойко А. Э., Техническая термодинамика, 2013, с. 172.
- ↑ Бахшиева Л. Т. и др., Техническая термодинамика и теплотехника, 2008, с. 148.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 95.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113.
- ↑ Румер Ю. Б., Рывкин М. Ш., Термодинамика, статистическая физика и кинетика, 2000, с. 35.
- ↑ 1 2 Крестовников А. Н., Вигдорович В. Н., Химическая термодинамика, 1973, с. 63.
Литература[править | править код]
- Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. – Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. – 102 p. (фр.)
- Бахшиева Л. Т., Кондауров Б. П., Захарова А. А., Салтыкова В. С. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. – 2-е изд., испр. – М.: Академия, 2008. – 272 с. – (Высшее профессиональное образование). – ISBN 978-5-7695-4999-1.
- Бэр Г. Д. Техническая термодинамика. – М.: Мир, 1977. – 519 с. (недоступная ссылка)
- Кинан Дж. Термодинамика / Пер с англ. А. Ф. Котина под ред. М. П. Вукаловича. – М.-Л.: Госэнергоиздат, 1963. – 280 с.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. – Издание 3-е, доп. – М.: Наука, 1976. – 584 с. – («Теоретическая физика», том V).
- Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. – 2-е изд., испр. и доп. – М.: Металлургия, 1973. – 256 с.
- Николаев Г. П., Лойко А. Э. Техническая термодинамика. – Екатеринбург: УрФУ, 2013. – 227 с.
- Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. – 2-е изд., испр. и доп. – Новосибирск: Изд-во Носиб. ун-та, 2000. – 608 с. – ISBN 5-7615-0383-2.
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. – М.: Астрель, 2001. – Т. 3. – 208 с. – 7000 экз. – ISBN 5-17-004585-9.
- Сивухин Д. В. Общий курс физики. – Т. II. Термодинамика и молекулярная физика. – 5 изд., испр.. – М.: ФИЗМАТЛИТ, 2005. – 544 с. – ISBN 5-9221-0601-5.
Источник
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
Подставляем значения и вычисляем:
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
Теперь можно рассчитать КПД:
Или, умножая на 100, получаем значение КПД в процентах:
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
По условию:
Вычислим сначала работу, а затем КПД:
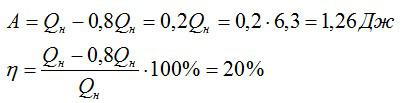
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
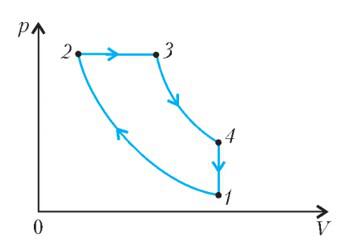
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1-2 и 3-4, изобары 2-3 и изохоры 4-1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
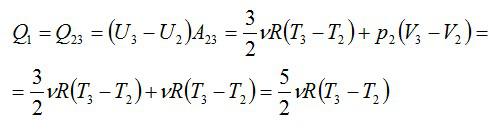
Аналогично:
Получим результат:
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
Отсюда:
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
Источник
Петр Иванович Дубровский, добросовестный инженер – исследователь, честный и непредвзятый частный научный детектив.
: d-pi@yandex.ru
Однажды некий Аристипп Киренейский (живший, согласно нынешней мифологии, почти 2400 лет тому назад, чему я не очень верю) высказал довольно разумную идею: “Детей надо учить тому, что пригодится им, когда они вырастут.” В связи с этим у меня вопрос – а зачем в школах и вузах детей учат “Циклу и теореме (теоремам) Карно” ?
Поэтому “Не лѣпо ли ны бяшетъ, братие, начяти старыми словесы трудныхъ повѣстий” о цикле Карно и так называемой «теореме» (иногда говорят – «теоремах») Карно, согласно которым КПД цикла Карно не зависит от природы рабочего тела и конструкции теплового двигателя и является функцией температур нагревателя и холодильника.
КПД = (T₂ – T₁)/T₂, где T₂ и T₁ – температуры «нагревателя» и «холодильника» соответственно.
При этом утверждается, что «КПД цикла Карно – максимально возможный из всех термодинамических циклов»
В комментариях к статье «Дело об ЭНЕРГИИ Исправление ошибок физики» одна из моих оппонентов, Ирина Юдакина пишет, цитирую: «цикл Карно имеет максимальный кпд при нулевой работе на выходе. До кучи в нем 2 изотермы, которые в железе не реализуемы. Удачи!»
И далее:
«Изотерма в железе не реализуема по причине невозможности полной передачи тепла между объектами. А изотерма требует именно полную передачу. Практические реализации содержат цепочку адиабат с изобарами. В общем случае, для реализации 1 процентного отклонения от изотермы нужно 100 ступеней».
Цикл Карно, если кто не помнит, это (цитирую барышню Вики, со ссылкой на «Физическую Энциклопедию» и «Общий курс физики» Д.В. Сивухина, Том II. Термодинамика и молекулярная физика., 5 издание, исправленное, Москва, ФИЗМАТЛИТ, 2005) это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой – холодильником.
Вообще ни один школьный курс физики и не один уважающий себя курс лекций по вузовской физике не обходится без цикла Карно и радостных восклицаний, что КПД цикла Карно никакому современному тепловому двигателю не переплюнуть.
Правда, из школьного курса физики нам известно, что КПД любой машины, системы, в том числе и «идеального двигателя системы Карно» равен КПД = А / Е, где
А – это совершенная машиной, двигателем или системой полезная работа, а
Е – это энергия, затраченная на совершение этой работы.
И вот тут интересно снова воспроизвести слова Ирины Юдакиной: «цикл Карно имеет максимальный кпд при нулевой работе на выходе. До кучи в нем 2 изотермы, которые в железе не реализуемы. Удачи!»
И тут я с Ириной почти полностью согласен. Но! В логике есть понятие контрадикторность. Контрадикторность (противоречие), если кто не знает, это логическое отношение между понятиями, одно из которых является отрицанием другого и между которыми не может быть третьего, среднего варианта. Рассмотрим первое предложение Ирины с точки зрения логики. В нём содержатся два утверждения:
1. Цикл Карно имеет максимальный КПД, то есть КПД = max
2. Цикл Карно имеет нулевую работу на выходе, то есть А = 0.
Согласно только что приведенной формуле КПД = А / Е = 0 / Е = 0. То есть Ирина в одном и том же предложении утверждает, что КПД = 0 – это и есть максимальный КПД. В формальной логике контрадикторность (противоречие) считается недопустимым. В предложении Ирины налицо явная контрадикторность, которая, естественно, должна быть каким-то образом разрешена. То есть какое-то одно из этих утверждений должно быть признано заведомо ложным. Какое же, Ирина? А вы, уважаемые читатели, помогите Ирине разобраться, какое же её утверждение следует признать ложным.
Есть довольно давняя английская поговорка, перекочевавшая в русский язык практически без изменений: «There are three things you can watch forever: fire, water, and other people working…», то есть: «существуют три вещи, на которые Вы можете смотреть вечно – огонь, вода и как другие люди работают. Есть вариант «There are three things you can watch forever: fire burning, water falling, other people working…», что можно перевести как «бесконечно можно смотреть на три вещи: горящий огонь, льющуюся воду и на работающих других людей».
В современном русском языке принято говорить так: «Бесконечно можно смотреть на три вещи: как горит огонь, как течёт вода и как работают другие люди». Я бы слегка подправил это высказывание: «Бесконечно можно смотреть на три вещи: как горит огонь, как течёт вода и как пытается заработать идеальный двигатель системы Карно».
Причем понятно, что огонь когда-нибудь потухнет, так как закончатся дрова, и «мы выпьем всю эту нефть и выкурим весь этот газ», как пел Юрий Шевчук. Понятно, что когда погаснет или взорвётся Солнце, перестанет литься вода, так как прекратится круговорот воды в природе.
Кстати, там, в статье по этой ссылке, есть два простых вопроса, на которые пока никто из школьных учителей, преподавателей вузов или академиков из РАН и РАО не смог дать ответа.
Но вот смотреть, как пытается заработать идеальный двигатель системы Карно, можно действительно смотреть вечно. Потому что он не заработает никогда. Я не буду приводить своих доводов, достаточно простых слов моего «оппонента» Ирины: «До кучи в нем [имеется в виду цикл Карно] 2 изотермы, которые в железе не реализуемы». То есть Ирина прямо заявляет, что идеальный двигатель системы Карно, даже имея «нулевую работу на выходе» и, соответственно, нулевой КПД, всё равно работать не может. Она объясняет это тем, что, цитирую: «Изотерма в железе не реализуема по причине невозможности полной передачи тепла между объектами. А изотерма требует именно полную передачу. Практические реализации содержат цепочку адиабат с изобарами. В общем случае, для реализации 1 процентного отклонения от изотермы нужно 100 ступеней».
Вообще-то причина невозможности «реализации в железе» цикла Карно заключается в том, что никаких «изотермических процессов» в природе попросту не может происходить. Закон, открытый монахом Эдмом Мариоттом и естествоиспытателем Бойлем, касался не «изотермических процессов», а соотношения давления и объёма одного и того же объёма газа, находящегося при одной и той же температуре. Никаких «изотермических процессов» в природе происходить не может, а значит, их не должно быть и в физике. Я пока до конца еще не разобрался, кто был тот самый бестолковый остолоп, который первым придумал и ввел в физику понятие «изотермический процесс», но больше всех в этой глупости я сейчас подозреваю именно Сади Карно.
В уже упомянутой мной песне про нефть и газ «просто Юры», как он однажды представился «светлейшему», есть такие слова:
«…И мы вновь научимся любить
И дружить со своей головой…»
Боюсь, нынешнее поколение физико-теоретиков, академиков ОФН РАН и РАО, чиновников из Министерства просвещения и Министерства высшего образования и науки уже не смогут «дружить со своей головой». Есть у меня слабенькая надежда, что со своей головой начнут дружить школьные учителя физики и преподаватели вузов… но очень слабенькая надежда. Которая, возможно, так никогда и не оправдается. Дело в том, что вот уже второе столетие подряд авторы школьных учебников так и продолжают переписывать бестолковые рассуждения из книги в книгу, из учебника в учебник, ни на йоту не задумавшись над их истинным смыслом. Причем это поветрие не обошло стороной даже «маститых ученых». Вот что, например, пишут признанные во всем мире «гении от теоретической физики» Л.Д. Ландау и Е.М. Лившиц в своём труде «Статистическая физика»:
«Процесс этот должен осуществляться таким образом, чтобы тела, между которыми происходит непосредственный обмен энергией, находились при одинаковой температуре. Именно, рабочее тело при температуре T₂ приводится в соприкосновение с телом с температурой T₂ и изотермически получает от него определенную энергию. Затем оно адиабатически охлаждается до температуры T₁, отдает при этой температуре энергию телу с температурой T₁, [надо понимать, снова изотермически?] и, наконец, адиабатически возвращается в первоначальное состояние. При расширениях, связанных с этим процессом, рабочее тело производит работу над внешними объектами. Описанный круговой процесс называется циклом Карно.» [8, глава 2, §19.]
Вы только вдумайтесь, что именно написали эти два «гения». Непосредственный обмен тепловой энергией между телами, газом (рабочее тело) и «нагревателем» при одинаковой температуре. В реальной жизни, если происходит непосредственный обмен тепловой энергией между телами, это приводит к нагреванию и охлаждению тел.
Например, чтобы вскипятить воду в чайнике, то чайник надо либо включить в сеть, чтобы стал нагреваться нагревательный элемент и передавал вырабатываемую им теплоту воду внутри чайника, либо поставить чайник на горящую газовую конфорку.
А что по сути предлагают гениальные теоретики Ландау и Лифшиц? Поставить холодный чайник на выключенную конфорку или смотреть на не включенный в сеть электрочайник в надежде, что он скоро закипит. Это будет вечный процесс… Соответственно, идеальный двигатель системы Карно, использующий в своей «работе» цикл Карно, является дважды вечным двигателем, так как подразумевает в течение одного цикла использовать два вечных «изотермических процесса».
Ландау и Лифшиц утверждают, что, цитирую «при расширениях, связанных с этим процессом, рабочее тело производит работу над внешними объектами»… интересно, какую? Если даже Ирина заметила, что цикл Карно имеет «нулевую работу на выходе». Опять налицо ситуация «Собака Шульца»? Кто-то, либо Ландау с Лифшицем, либо Ирина Юдакина врет? Читатели, помогите разобраться. Лично я в данном вопросе – на стороне Ирины.
Я предлагаю собрать вместе всех авторов, которые описывают «самый эффективный цикл Карно» в своих «умных книжках», в том числе и в школьных учебниках, и посадить их перед не включенными в сеть электрическими чайниками в ожидании, когда вода внутри начнёт кипеть. И начать кормить их только тогда, когда они либо вскипятят воду в чайниках силой своей гениальной мысли, либо напишут объяснительные с текстом «извините меня, я признаю, что был полным остолопом и писал свою «умную книжку для школьников или студентов, отключив свой мозг». Полагаю, это будет справедливо.
Кстати, насчёт «практической реализации» цикла Карно, предложенной Ириной: «Практические реализации содержат цепочку адиабат с изобарами. В общем случае, для реализации 1 процентного отклонения от изотермы нужно 100 ступеней». Конечно, это будет уже не цикл Карно, а некий другой цикл, использующий «цепочки адиабат с изобарами», но всё же.
Физика, как я уже неоднократно писал, ссылаясь на авторитетных академиков АН СССР, есть, прежде всего, «экспериментальная наука». Так, может быть, Ирина возьмётся за проведение опыта, который докажет, что «идеальный двигатель системы Карно», который будет работать по циклу, максимально приближённому к циклу Карно, имеет самый высокий КПД в заданном диапазоне температур?
На самом деле 98% современной «теоретической термодинамики» – это псевдонаучные фантазии бестолковых физико-теоретиков, не имеющих отношения к реальной термодинамике. И начинать надо с того, что полностью исключить из школьных учебников все фантазийные циклы Карно и прочие глупости, заменив этот раздел «Основами практической теплотехники». Так мы хотя бы не будем забивать головы школьников, следующему поколению людей, бестолковыми догматами и ложными стереотипами. Но, как я уже сказал, нынешнее поколение физико-теоретиков, академиков ОФН РАН и РАО, чиновников из Министерства просвещения и Министерства высшего образования и науки вряд ли начнут в обозримом будущем «дружить со своей головой».
ЭТО ТОЛЬКО САМОЕ НАЧАЛО. У МЕНЯ ЕСТЬ МНОГО ЧЕГО СКАЗАТЬ ПО ПОВОДУ «СОВРЕМЕННОЙ ТЕОРЕТИЧЕСКОЙ ТЕРМОДИНАМИКИ», ОСНОВАННОЙ НА ГЛУПОСТЯХ И ЗАБЛУЖДЕНИЯХ ДВУХСОТЛЕТНЕЙ ДАВНОСТИ.
МНОГОЧИСЛЕННЫЕ ПРОДОЛЖЕНИЯ, РАЗУМЕЕТСЯ ПОСЛЕДУЮТ.
Должен сказать, что люди потихоньку просыпаются, читаем:
На смерть Сади Карно. Энергетический баланс термодинамического цикла.
Источник