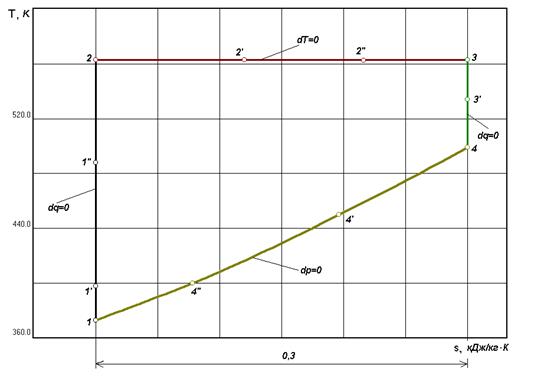
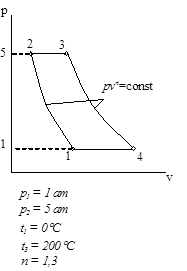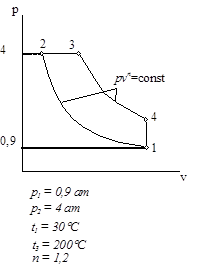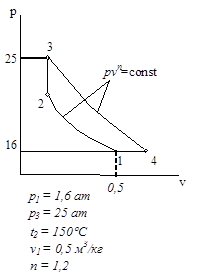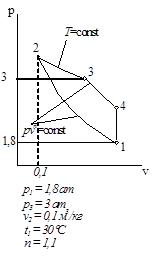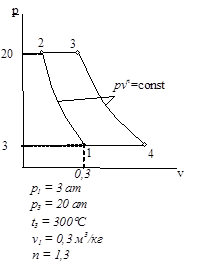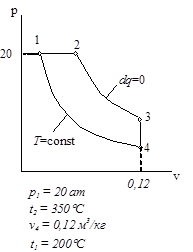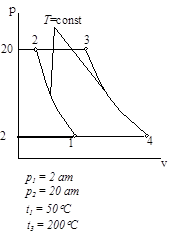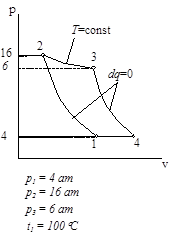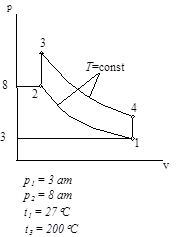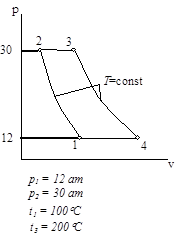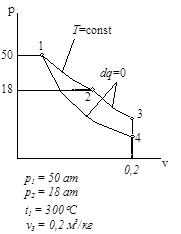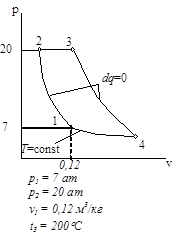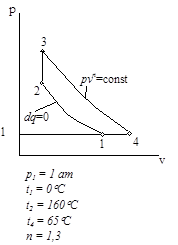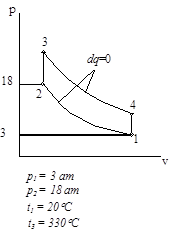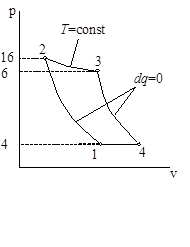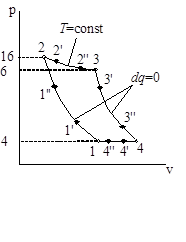Циклы газово тепловых двигателей

В термодинамике цикл Карно́ или процесс Карно́ – это идеальный[1]круговой процесс, состоящий из двух адиабатных и двух изотермических процессов[2]. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой – холодильником[3].
Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году[4][5].
Поскольку идеальные процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности.
Коэффициент полезного действия (КПД) любой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника[6]. По этой причине, позволяя оценить верхний предел КПД тепловой машины, цикл Карно важен для теории тепловых машин. В то же время КПД цикла Карно настолько чувствителен к отклонениям от идеальности (потерям на трение), что данный цикл никогда не применяли в реальных тепловых машинах[K 1][8].
Описание цикла Карно[править | править код]
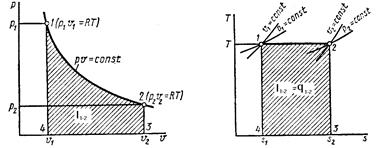
Рис. 1. Цикл Карно в координатах T-S
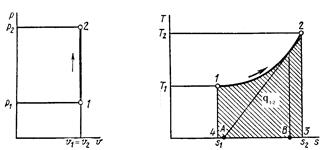
Рис. 2. Цикл Карно в координатах p-V
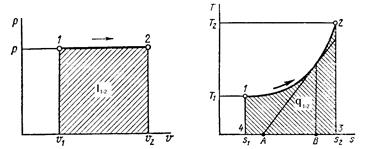
Рис. 3. Цикл Карно на термодинамической поверхности идеального газа
Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две – при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах (температура) и (энтропия).
1. Изотермическое расширение (на рис. 1 – процесс A→B). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты , то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
2. Адиабатическое расширение (на рис. 1 – процесс B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника , тело совершает механическую работу, а энтропия остаётся постоянной.
3. Изотермическое сжатие (на рис. 1 – процесс C→D). Рабочее тело, имеющее температуру , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты . Над телом совершается работа, его энтропия уменьшается.
4. Адиабатическое сжатие (на рис. 1 – процесс D→A). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
Обратный цикл Карно[править | править код]
В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий[9][10]: адиабатического сжатия за счёт совершения работы (на рис. 1 – процесс C→B); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 – процесс B→A); адиабатического расширения (на рис. 1 – процесс A→D); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 – процесс D→C).
КПД тепловой машины Карно[править | править код]
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
Первая и вторая теоремы Карно[править | править код]
Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно[11]. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно[12][13]. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.
Связь между обратимостью цикла и КПД[править | править код]
Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.
Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД[14]. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например цикл Эрикссона (англ.)русск., состоящий из двух изобар и двух изотерм[14].
Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.
См. также[править | править код]
- Термодинамические циклы
- Первое начало термодинамики
- Второе начало термодинамики
- Термодинамическая энтропия
- Термодинамические потенциалы
Комментарии[править | править код]
- ↑ В реальных тепловых машинах цикл Карно не используют, поскольку практически невозможно осуществить процессы изотермического сжатия и расширения. Кроме того, полезная работа цикла, представляющая собой алгебраическую сумму работ во всех четырех составляющих цикл частных процессах, даже в идеальном случае полного отсутствия потерь мала по сравнению с работой в каждом из частных процессов, то есть мы имеем дело с обычной ситуацией, когда итоговый результат представляет собой малую разность больших величин. Применительно к математическим вычислениям это означает высокую отзывчивость результата даже на небольшие вариации значений исходных величин, а в рассматриваемом нами случае соответствует высокой чувствительности полезной работы цикла Карно и его КПД к отклонениям от идеальности (потерям на трение). Эта связь с отклонениями от идеальности настолько велика, что с учетом всех потерь полезная работа цикла Карно приближается к нулю[7].
Примечания[править | править код]
- ↑ То есть без потерь, в первую очередь на трение.
- ↑ Карно цикл // Италия – Кваркуш. – М. : Советская энциклопедия, 1973. – (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969-1978, т. 11).
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 94.
- ↑ Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. – Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. – 102 p. (фр.)
- ↑ Второе начало термодинамики. (Работы Сади Карно – В. Томсон – Кельвин – Р. Клаузиус – Л. Больцман – М. Смолуховский) / Под. ред. А. К. Тимирязева. – Москва-Ленинград: Государственное технико-теоретическое издательство, 1934. – С. 17-61.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113-114.
- ↑ Бэр Г. Д., Техническая термодинамика, 1977, с. 112.
- ↑ Кинан Дж., Термодинамика, 1963, с. 93.
- ↑ Николаев Г. П., Лойко А. Э., Техническая термодинамика, 2013, с. 172.
- ↑ Бахшиева Л. Т. и др., Техническая термодинамика и теплотехника, 2008, с. 148.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 95.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113.
- ↑ Румер Ю. Б., Рывкин М. Ш., Термодинамика, статистическая физика и кинетика, 2000, с. 35.
- ↑ 1 2 Крестовников А. Н., Вигдорович В. Н., Химическая термодинамика, 1973, с. 63.
Литература[править | править код]
- Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. – Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. – 102 p. (фр.)
- Бахшиева Л. Т., Кондауров Б. П., Захарова А. А., Салтыкова В. С. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. – 2-е изд., испр. – М.: Академия, 2008. – 272 с. – (Высшее профессиональное образование). – ISBN 978-5-7695-4999-1.
- Бэр Г. Д. Техническая термодинамика. – М.: Мир, 1977. – 519 с. (недоступная ссылка)
- Кинан Дж. Термодинамика / Пер с англ. А. Ф. Котина под ред. М. П. Вукаловича. – М.-Л.: Госэнергоиздат, 1963. – 280 с.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. – Издание 3-е, доп. – М.: Наука, 1976. – 584 с. – («Теоретическая физика», том V).
- Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. – 2-е изд., испр. и доп. – М.: Металлургия, 1973. – 256 с.
- Николаев Г. П., Лойко А. Э. Техническая термодинамика. – Екатеринбург: УрФУ, 2013. – 227 с.
- Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. – 2-е изд., испр. и доп. – Новосибирск: Изд-во Носиб. ун-та, 2000. – 608 с. – ISBN 5-7615-0383-2.
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. – М.: Астрель, 2001. – Т. 3. – 208 с. – 7000 экз. – ISBN 5-17-004585-9.
- Сивухин Д. В. Общий курс физики. – Т. II. Термодинамика и молекулярная физика. – 5 изд., испр.. – М.: ФИЗМАТЛИТ, 2005. – 544 с. – ISBN 5-9221-0601-5.
Источник
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Источник
Термодинами́ческие ци́клы – круговые процессы в термодинамике, то есть такие процессы, в которых совпадают начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура и энтропия).
Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу.
Компонентами любой тепловой машины являются рабочее тело, нагреватель и холодильник (с помощью которых меняется состояние рабочего тела).
Обратимым называют цикл, который можно провести как в прямом, так и в обратном направлении в замкнутой системе. Суммарная энтропия системы при прохождении такого цикла не меняется. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы (например, цикл Стирлинга и цикл Эрикссона (англ.)), в которых обратимость достигается путём введения дополнительного теплового резервуара – регенератора. Общим (т.е. указанные циклы частный случай) для всех этих циклов с регенерацией является Цикл Рейтлингера. Можно показать (см. статью Цикл Карно), что обратимые циклы обладают наибольшей эффективностью.
Основные принципы[править | править код]
Прямое преобразование тепловой энергии в работу запрещается постулатом Томсона (см. Второе начало термодинамики). Поэтому для этой цели используются термодинамические циклы.
Для того, чтобы управлять состоянием рабочего тела, в тепловую машину входят нагреватель и холодильник. В каждом цикле рабочее тело забирает некоторое количество теплоты () у нагревателя и отдаёт количество теплоты холодильнику. Работа, совершённая тепловой машиной в цикле, равна, таким образом,
,
так как изменение внутренней энергии в круговом процессе равно нулю (это функция состояния).
Напомним, что работа не является функцией состояния, иначе суммарная работа за цикл также была бы равна нулю.
При этом нагреватель потратил энергию . Поэтому тепловой, или, как его ещё называют, термический или термодинамический коэффициент полезного действия тепловой машины (отношение полезной работы к затраченной тепловой энергии) равен
.
Вычисление работы и КПД в термодинамическом цикле[править | править код]
Работа в термодинамическом цикле, по определению, равна
,
где – контур цикла.
C другой стороны, в соответствии с первым началом термодинамики, можно записать
.
Аналогичным образом, количество теплоты, переданное нагревателем рабочему телу, равно
.
Отсюда видно, что наиболее удобными параметрами для описания состояния рабочего тела в термодинамическом цикле служат температура и энтропия.
Цикл Карно и максимальный КПД тепловой машины[править | править код]
Основная статья: Цикл Карно.
Цикл Карно в координатах T и S
Представим себе следующий цикл:
Фаза А→Б. Рабочее тело с температурой, равной температуре нагревателя, приводится в контакт с нагревателем. Нагреватель сообщает рабочему телу тепла в изотермическом процессе (при постоянной температуре), при этом объём рабочего тела увеличивается.
Фаза Б→В. Рабочее тело отсоединяется от нагревателя и продолжает расширяться адиабатически (без теплообмена с окружающей средой). При этом его температура уменьшается до температуры холодильника.
Фаза В→Г. Рабочее тело приводится в контакт с холодильником и передает ему тепла в изотермическом процессе. При этом объём рабочего тела уменьшается.
Фаза Г→А. Рабочее тело адиабатически сжимается до исходного размера, и его температура увеличивается до температуры нагревателя.
Его КПД равен, таким образом,
,
то есть, зависит только от температур холодильника и нагревателя. Видно, что 100%-ный КПД можно получить только в том случае, если температура холодильника есть абсолютный нуль, что недостижимо.
Можно показать, что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бо́льшим КПД.
Заметим, что мощность тепловой машины Карно равна нулю, так как передача тепла в отсутствие разности температур идёт бесконечно медленно.
См. также[править | править код]
- Тепловая машина
- Рабочее тело
- Цикл Карно
- Бинарные циклы
Ссылки[править | править код]
- Интерактивный сетевой расчет и графическая иллюстрация основных термодинамических циклов
- Программа Расчет термодинамических циклов
Литература[править | править код]
- Базаров И. П. Термодинамика. (недоступная ссылка) М.: Высшая школа, 1991, 376 с.
- Базаров И. П. Заблуждения и ошибки в термодинамике. Изд. 2-ое испр. М.: Едиториал УРСС, 2003. 120 с.
- Дыскин Л.М., Пузиков Н.Т. Расчет термодинамических циклов.
- Квасников И. А. Термодинамика и статистическая физика. Т.1: Теория равновесных систем: Термодинамика. Том.1. Изд. 2, испр. и доп. М.: УРСС, 2002. 240 с.
- Сивухин Д. В. Общий курс физики. – М.: Наука, 1975. – Т. II. Термодинамика и молекулярная физика. – 519 с.
- Александров А. А. Термодинамические основы циклов теплоэнергетических установок. Издательство МЭИ, 2004.
Источник
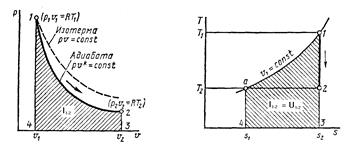
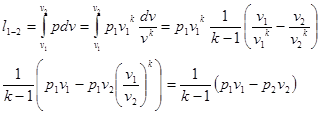 (22)
(22)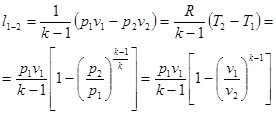 (23)
(23)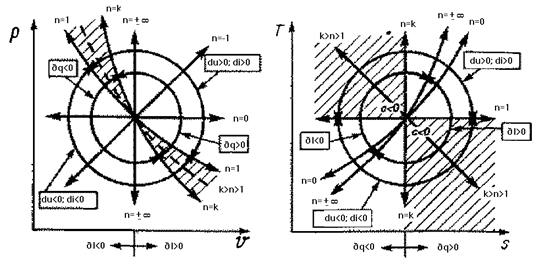
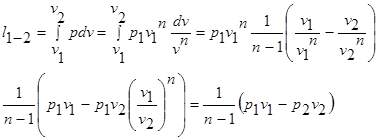 (29)
(29)