Цикл пока словесное описание
Цель: изучение алгоритмической структуры циклы, создание моделей и алгоритмов для решения практических задач.
Ход урока
I. Актуализация знаний
- Повторить понятие алгоритма, основные конструкции алгоритмического языка.
- Уметь разрабатывать математическую модель, алгоритм и блок схему решения задачи.
- Иметь понятие о языках программирования и их назначении.
- Уметь работать в среде программирования.
- Знать структуры программы.
- Уметь записывать выражения, содержащие числовые и символьные величины.
- Знать структуры операторов и особенности их работы.
- Уметь применять операторы при написании программ с линейными и ветвящимися структурами.
- Уметь на компьютере создавать и запускать программы на отладку.
II. Теоретический материал урока
Большинство практических задач требует многократного повторения одних и тех же действий, т. е. повторного использования одного или нескольких операторов. (Презентация)
Пусть требуется ввести и обработать последовательность чисел. Если чисел всего пять, можно составить линейный алгоритм. Если их тысяча, записать линейный алгоритм можно, но очень утомительно и нерационально. Если количество чисел к моменту разработки алгоритма неизвестно, то линейный алгоритм принципиально невозможен.
Другой пример. Чтобы найти фамилию человека в списке, надо проверить первую фамилию списка, затем вторую, третью и т.д. до тех пор, пока не будет найдена нужная или не будет достигнут конец списка. Преодолеть подобные трудности можно с помощью циклов.
Циклом называется многократно исполняемый участок алгоритма (программы). Соответственно циклический алгоритм — это алгоритм, содержащий циклы.
Различают два типа циклов: с известным числом повторений и с неизвестным числом повторений. При этом в обоих случаях имеется в виду число повторений на стадии разработки алгоритма.
Существует 3 типа циклических структур:
- Цикл с предусловием;
- Цикл с послеусловием;
- Цикл с параметром;
Иначе данные структуры называют циклами типа «Пока», «До», «Для».
Графическая форма записи данных алгоритмических структур:
Цикл с предусловием (иначе цикл пока) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| Пока (условие) нц серия команд кц | while условие do begin серия команд; end; |
где
условие – выражение логического типа.
Цикл может не выполняться ни разу, если значение логического выражения сразу же оказывается ложь.
Серия команд, находящихся между begin и end, выполняются до тех пор, пока условие истинно.
Для того чтобы цикл завершился, необходимо, чтобы последовательность инструкций между BEGIN и END изменяла значение переменных, входящих в условие.
Цикл с постусловием (иначе цикл до) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| В алгоритмическом языке нет команды которая могла бы описать данную структуру, но ее можно выразить с помощью других команд (Например, ветвления). | repeat серия команд until условие |
где
условие – выражение логического типа.
Обратите внимание:
Последовательность инструкций между repeat и until всегда будет выполнено хотя бы один раз;
Для того чтобы цикл завершился, необходимо, чтобы последовательность операторов между repeat и until изменяла значения переменных, входящих в выражение условие.
Инструкция repeat, как и инструкция while, используется в программе, если надо провести некоторые повторяющиеся вычисления (цикл), однако число повторов заранее не известно и определяется самим ходом вычисления.
Цикл с параметром (иначе цикл для) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| Для i от а до b шаг h делай Нц Серия команд кц | h = +1 for i:= a to b do begin серия команд end; h = -1 for i:= b downto a do begin Cерия команд; end; |
где
i – параметр цикла;
a – начальное значение цикла;
b – конечное значение цикла;
h – шаг изменения параметра.
Структура данного цикла иначе называют циклом i раз.
Эта команда выполняется таким образом: параметру i присваивается начальное значение а, сравнивается с конечным значением b и, если оно меньше или равно конечному значению b, выполняется серия команд. Параметру присваивается значение предыдущего, увеличенного на величину h – шага изменения параметра и вновь сравнивается с конечным значением b.
На языке программирования Паскаль шаг изменения параметра может быть равным одному или минус одному.
Если между begin и end находится только один оператор, то операторные скобки можно не писать. Это правило работает для цикла типа «Пока» и «Для».
Рассмотрим пример решения задач с использованием данных структур
Пример.
Вычислить произведение чисел от 1 до 5 используя различные варианты цикла
Математическая модель:
Р= 1· 2· 3· 4· 5=120
Составим алгоритм в виде блок-схемы.
Для проверки правильности алгоритма заполним трассировочную таблицу.
| Шаг | Операция | Р | i | Проверка условия |
| 1 | P:=1 | 1 | ||
| 2 | i:=1; | 1 | 1 | |
| 3 | i<=5 P:=P*I i:=i+1 | 1 | 1 | 1<=5, да (истина) |
| 4 | i<=5 P:=P*I i:=i+1 | 2 | 2 | 2<=5, да (истина) |
| 5 | i<=5 P:=P*I i:=i+1 | 6 | 3 | 3<=5, да (истина) |
| 6 | i<=5 P:=P*I i:=i+1 | 24 | 4 | 4<=5, да (истина) |
| 7 | i<=5 P:=P*I i:=i+1 | 120 | 5 | 5<=5, да (истина) |
| 8 | i<=5 P:=P*I i:=i+1 | 6<=5, нет (ложь) |
Проверка условия происходит в несколько шагов: проверка условия и выполнение команд на одной из ветвей. Поэтому в трассировочной таблице записываются не команды алгоритма, а отдельные операции, выполняемые компьютером на каждом шаге.
Шаг первый: Р присваивается значение один.
Шаг второй: i присваивается значение один.
Шаг третий: при i равном единице проверяем условие один меньше или равен пяти, да, условие истинно, значит Р присваивается значение один умноженное на один, будет два. Для i: один плюс один, будет два.
Шаг четвертый: при i равном двум проверяем условие два меньше или равен пяти, да, условие истинно, значит Р присваивается значение 2 умноженное на один, будет 2. Для i: два плюс один, будет три.
Шаг пятый: при i равном трем проверяем условие три меньше или равен пяти, да, условие истинно, значит Р присваивается значение два умноженное на три, будет шесть. Для i: три плюс один, будет четыре.
Шаг шестой: при i равном четырем проверяем условие четыре меньше или равен пяти, да, условие истинно, значит Р присваивается значение шесть умноженное на четыре, будет двадцать четыре. Для i: четыре плюс один, будет пять.
Шаг седьмой: при i равном пяти проверяем условие пять меньше или равен пяти, да ,условие истинно, значит Р присваивается значение двадцать четыре умноженное на пять, будет сто двадцать. Для i: пять плюс один, будет шесть.
Шаг восьмой: при i равном шести проверяем условие шесть меньше или равен пяти, нет, условие ложно, тогда мы выходим из цикла, а в результате получаем последнее значение равное сто двадцати.
Program Pr1;
Var i: integer;
Begin
P:=1;
i:=1;
While i<=5 do
begin
P:=P*i;
i:=i+1;
end;
Write (‘P=’, P);
end.
Для цикла с постусловием построим блок-схему и трассировочную таблицу. (слайд16)
В результате получаем последнее значение равное сто двадцати на седьмом шаге
И для Цикла с параметром построим блок-схему и трассировочную таблицу. (слайд17)
В результате получаем последнее значение равное сто двадцати на шестом шаге
Задача:
Вывести на экран числа от 1 до 5 в:
- прямом порядке;
- обратном порядке.
Математическая модель:
- 1 2 3 4 5;
- 5 4 3 2 1.
Блок-схема и программа решения задачи представлена для чисел в прямом порядке и обратном порядке.
(слайд 21)
Запишем рассмотренные алгоритмы на языке программирования Паскаль.
(слайд 22)
III. Подведение итогов урока
И так мы рассмотрели следующие вопросы:
- Алгоритмическая структура цикл;
- Виды алгоритмических структур:
- Цикл с предусловием;
- Цикл с послеусловием;
- Цикл с параметром;
- Рассмотрели способы записи данных структур;
- Разобрали примеры решения задач с помощью этих структур.
Источник
Цикл «пока»
А теперь попробуем написать программу для решения очень простой задачи: закрасить все клетки справа от Робота (рис. 3.13).
Рис. 3.13
Правда, сколько именно клеток следует закрасить, не уточнено. Известно только, что:
1) справа на неизвестном расстоянии есть стена;
2) клетки нужно красить, пока Робот не подойдет к стене вплотную.
Воспользуемся тем, что Робот может анализировать и сообщать обстановку вокруг себя, проверяя следующие простые условия:
справа свободно
слева свободно
сверху свободно
снизу свободно
закрашено
Ясно, что пока будет выполняться условие справа свободно, нужно выполнять команды:
вправо
закрась
Для оформления таких последовательностей действий используется специальная конструкция алгоритмического языка — цикл «пока».
ПОКА справа свободно ДЕЛАТЬ
вправо
закрась
КОНЕЦ
В общем виде цикл «пока» записывается так:
ПОКА <условие> ДЕЛАТЬ
<тело цикла (последовательность команд)>
КОНЕЦ
Блок-схема цикла «пока» имеет вид, показанный на рис. 3.14.
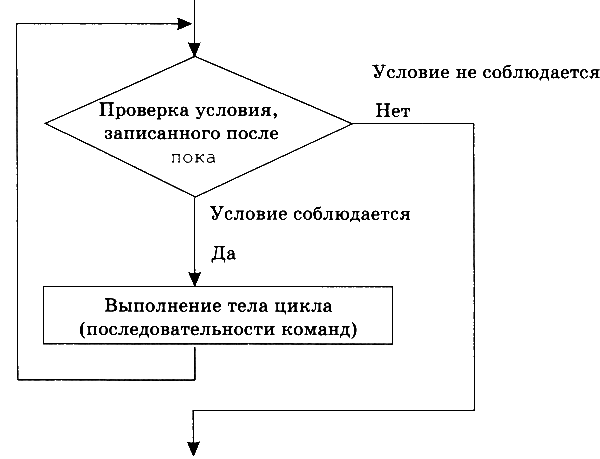
Рис. 3.14
При выполнении этого цикла исполнитель повторяет следующие действия:
1) проверяет записанное после служебного слова ПОКА условие;
2) если условие не соблюдается (Робот ответил «Нет»), то выполнение цикла прекращается, и Робот начинает выполнять команды, записанные после служебного слова КОНЕЦ. Если же условие соблюдается (Робот ответил «Да»), то Робот выполняет тело цикла и снова проверяет условие.
Напишем программу, исполняя которую Робот нарисует на клетчатом поле меандр (рис. 3.12), число витков которого зависит от положения правой стены.
Виток меандра умещается на клетчатом поле, если между клеткой, занимаемой Роботом, и правой стеной есть 1 клетка.
ПОКА справа свободно ДЕЛАТЬ
вправо
закрась; влево
закрась; влево
закрась; вверх
закрась; вверх
закрась; вправо; закрась
вправо; вправо; вправо
вниз; вниз
КОНЕЦ
В зависимости от исходного положения Робота тело цикла пока может не выполниться ни разу. Такая ситуация не является отказом.
♦ Подумайте, каким должно быть исходное положение Робота в программе рисования меандра, чтобы тело цикла не выполнилось ни разу.
Из-за логических ошибок, допущенных при составлении алгоритма, может возникнуть ситуация зацикливания. Это значит, что условие будет всегда соблюдаться, и выполнение цикла «пока» никогда не завершится.
Рассмотрим следующий пример:
ПОКА справа свободно ДЕЛАТЬ
вправо; влево
КОНЕЦ
♦ Что будет происходить, если справа от Робота нет стены?
Условие в цикле «пока» проверяется только перед выполнением тела цикла, но не в процессе его выполнения.
♦ Подумайте, что произойдет, если Робот начнет выполнять нашу программу рисования меандра с циклом «пока», находясь в следующем исходном положении:

♦ Что общего у циклов «повторить п раз» и «пока»? Какие между ними отличия? Нужны ли две конструкции для описания повторяющихся действий?
Простые и составные условия
В цикле «пока» могут использоваться не только простые, но и составные условия.
Составное условие образуется из одного или несколь¬ких простых условий и служебных слов И, ИЛИ, НЕ.
Рассмотрим составное условие А И В, где А, В — простые условия. Условие А И В выполнено, когда выполнено каждое из двух входящих в него простых условий.
Пусть А — простое условие сверху свободно, В — простое условие справа свободно. Рассмотрим подробно проверку составного условия А ИВ — сверху свободно и справа свободно
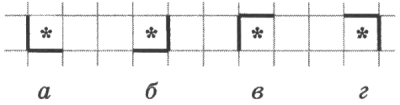
(рис. 3.15).
В случае а выполнено условие А (сверху свободно), выполнено условие В (справа свободно). Составное условие А И В(сверху свободно И справа свободно)также выполнено.
В случае б выполнено условие А, условие В не выполнено. Составное условие А И В не выполнено.
В случае в не выполнено условие А, условие В выполнено. Составное условие А И В не выполнено.
В случае г не выполнено условие А, не выполнено условие В. Составное условие А И В не выполнено.
♦ Нужно ли проверять условие В в составном условии АИВ, если условие А не выполнено?
Составное условие А ИЛИ В выполнено, когда выполнено хотя бы одно из двух входящих в него простых условий.
Рассмотрим проверку составного условия А ИЛИ В — сверху свободно ИЛИ справа свободно (см. рис. 3.15).
В случае а выполнено условие А (сверху свободно), выполнено условие В (справа свободно). Составное условие А ИЛИ В (сверху свободно ИЛИ справа свободно) выполнено.
В случае б выполнено условие А, не выполнено условие В. Составное условие А ИЛИ В выполнено.
В случае в не выполнено условие А, выполнено условие В. Составное условие А ИЛИ В выполнено.
В случае г не выполнено условие А, не выполнено условие В. Составное условие А ИЛИ В не выполнено.
♦ Нужно ли проверять условие В в составном условии А ИЛИ В, если условие А выполнено?
Составное условие НЕ А выполнено, когда не выполнено условие А.
Пусть А — простое условие закрашено. Рассмотрим проверку составного условия НЕ А (рис. 3.16).
рис. 3.16
В случае а условие А выполнено, условие НЕ А (НЕ закрашено) не выполнено.
В случае б условие А не выполнено, условие НЕ А (НЕ закрашено) выполнено.
Рассмотрим пример использования составного условия.
Известно, что Робот находится где-то в вертикальном коридоре. Ни одна из клеток коридора не закрашена.
Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернется в исходное положение.
Так как Роботу предстоит закрасить только клетки коридора, мы должны «научить» его их распознавать. Чем же клетки коридора отличаются от всех прочих клеток поля? Из рис. 3.17 видно, что каждая клетка коридора слева и справа ограничена стеной.
Робот находится в коридоре, пока слева стена и справа стена. В СКИ нашего исполнителя такие условия не предусмотрены. Там есть противоположные условия: слева свободно, справа свободно. Используем служебное слово НЕ:
слева стена → НЕ слева свободно
справа стена → НЕ справа свободно
Нужное условие примет вид:
НЕ слева свободно И НЕ справа свободно.
Представим план действий Робота укрупненными шагами (рис. 3.18):
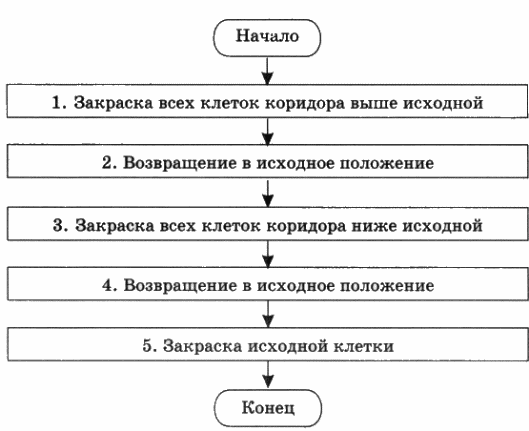
рис. 3.18
Для простоты предположим, что над коридором и под коридором есть хотя бы по одной клетке без стен (иначе придется делать дополнительные проверки сверху свободно, снизу свободно).
1. Чтобы закрасить все клетки коридора, находящиеся выше Робота, прикажем Роботу шагнуть вверх и выполним цикл «пока»:
вверх
ПОКА НЕ слева свободно И НЕ справа свободно ДЕЛАТЬ
закрась
вверх
КОНЕЦ
Под управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся выше от него, и окажется на клетке рядом с верхней границей коридора.
♦ При каком исходном положении Робота этот цикл не выполнится ни разу?
2. Командой вниз вернем Робота в коридор. Наша задача — вернуть его в исходную точку. Эта точка имеет единственный отличительный признак — она не закрашена. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вниз:
вниз
ПОКА закрашено ДЕЛАТЬ
вниз
КОНЕЦ
Под управлением этого алгоритма Робот окажется в исходной клетке.
3. Выполнив команду вниз, Робот пройдет исходную клетку и займет первую клетку, расположенную ниже исходной. Теперь можно закрашивать клетки коридора, расположенные ниже исходной:
вниз
ПОКА НЕ слева свободно И НЕ справа свободно
ДЕЛАТЬ
закрась
вниз
КОНЕЦ
♦ Возможна ли ситуация, что этот цикл не выполнится ни разу?
4. Так как, выполнив предыдущий алгоритм, Робот окажется под коридором, командой вверх вернем его в коридор. Возвращение в исходную точку обеспечивается алгоритмом:
вверх
ПОКА закрашено ДЕЛАТЬ
вверх
КОНЕЦ
5. По команде закрась Робот закрашивает исходную точку.
Полностью программа управления Роботом выглядит так:
вверх
ПОКА НЕ слева свободно И НЕ справа свободно
ДЕЛАТЬ
закрась
вверх
КОНЕЦ
вниз
ПОКА закрашено ДЕЛАТЬ
вниз
КОНЕЦ
вниз
ПОКА НЕ слева свободно И НЕ справа свободно
ДЕЛАТЬ
закрась
вниз
КОНЕЦ
вверх
ПОКА закрашено ДЕЛАТЬ
вверх
КОНЕЦ
закрась
Источник
Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.
Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.
При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.
В процессе разработки алгоритма решения задачи можно выделить следующие этапы:
- Этап 1 . Математическое описание решения задачи.
- Этап 2 . Определение входных и выходных данных.
- Этап 3 . Разработка алгоритма решения задачи.
Базовые алгоритмические конструкции
В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл-пока (циклический алгоритм).
Линейные алгоритмы
Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

Пример
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.
На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:
,
где с-длина гипотенузы, a, b – длины катетов.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
| На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.
|
Разветвляющиеся алгоритмы
Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Пример
ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.
Этап 1. Математическое описание решения задачи.
Из курса математики известно, если x > y, то наибольшее число x, если x < y, то наибольшее число y, если x = y, то число x равно числу y.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения чисел x и y. Выходным данными являются:
- наибольшее число
- любое из чисел, если числа равны
Для решения задачи нам необходимо знать значения x и y.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
|
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма
В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:
- первая: это элементы 1, 2, 3, 4, 8.
- вторая: это элементы 1, 2, 3, 5, 6, 8
- третья: это элементы 1, 2, 3, 5, 7, 8.
Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.
Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.
Циклические алгоритмы
Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.
При разработке алгоритма циклической структуры выделяют следующие понятия:
- параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
- начальное и конечное значения параметров цикла;
- шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.
Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:
- начальные значения цикла;
- конечные значения цикла;
- шаг цикла.
В тело цикла входят:
- многократно повторяющиеся действия для вычисления искомых величин;
- подготовка следующего значения параметра цикла;
- подготовка других значений, необходимых для повторного выполнения действий в теле цикла.
В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.
Пример
ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.
Этап 1. Математическое описание решения задачи.
Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:
где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.
Этап 2. Определение входных и выходных данных.
Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.
Выходные данные – значение суммы членов последовательности натуральных чисел.
Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.
Подготовка цикла заключается в задании начального и конечного значений параметра цикла.
- начальное значение параметра цикла равно 1,
- конечное значение параметра цикла равно n,
- шаг цикла равен 1.
Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.
Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:
S=S+i; I=I+1;
Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.
Этап 3. Разработка алгоритма решения задачи.
Введем обозначения: S – сумма последовательности, i – значение натурального числа.
Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
| В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма. Номера элементов соответствуют номерам шагов словесного описания алгоритма.
|
Источник


