Цикл for в матлаб

ОСНОВЫ ПРОГРАМИРОВАНИЯ В MATLAB 1

Операторы цикла В MATLAB повторяющиеся действия осуществляются с помощью операторов циклов for и while. Самое простое использование for осуществляется следующим образом: 2

For count = start: step: final Команды MATLAB End Здесь count – переменная цикла; n start, final – начальное и конечное действительное значение; n step – шаг из множества действительных чисел (по умолчанию равен 1, его можно опустить). Цикл заканчивается, как становиться больше final. только count 3

Пример 1 Вычислить сумму при x= -1, 0, 1. Решение В редакторе M-file создадим файл-программу. Сохраняем её в файле Summa. m S = 0; for k = 1 : 10 S = S + x. ^ k / factorial(k); End S В командной строке x = -1: 1: 1; Summa S = -0. 6 0 1. 7 Заметим, что переменные k, s глобальные. 4

Удобнее для этого примера использовать файлфункцию. В редакторе М-файлов В командной строке создаем файл-функцию S = funsum(x, N) > f = funsum (-1 : 1, 10) S = 0; > f = for m = 1 : N -0. 6 0 1. 7 S = S + x. ^ m / factorial(m); end Здесь переменные s, m локальные. 5

Пример 2 Создать матрицу Гильберта порядка n. Решение n = 4; a = zeros (n, n); for i = 1 : n for j = 1: n a (i, j) = 1 / (i+j-1); end a 6

Замечание Перед заполнением матриц и векторов следует сначала создать их и заполнить нулями командой zeros, для увеличения скорости алгоритма (то есть a = zeros (n, n) быстрее, чем a(i, j) = 0, i, j = 1, …, n). 7

Цикл for оказывается полезным, при выполнении повторяющихся действий, когда их число заранее известно. В случае, если их число заранее неизвестно можно воспользоваться циклом while: While условие цикла Команды MATLAB Еnd 8

Пример 3 Найти сумму ряда для заданного x До бесконечности суммировать не удастся, но можно накапливать сумму, пока слагаемые не будут слишком маленькими, например, пока 9

Замечание Малость слагаемого – понятие относительное, слагаемое, может быть, скажем, порядка 10 -10, но и сама сумма того же порядка. В этом случае нельзя останавливать суммирование. Не будем пока обращать на это внимание и вернемся к решению. 10

M-file функция В командной строке S = mysin(x) > f = mysin (1) S = 0; 0. 8415 k = 0; while abs(x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10 S = S + (-1)^k * x. ^ (2*k + 1)/factorial(2*k + 1); k = k + 1; end 11

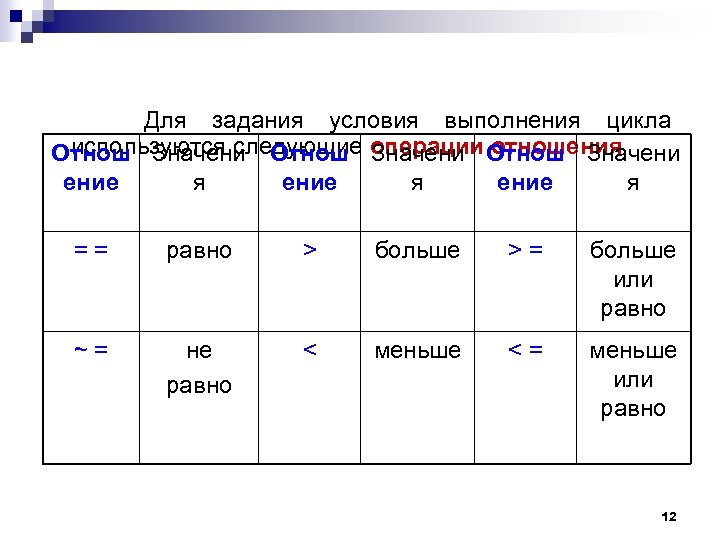Для задания условия выполнения цикла используются следующие операции отношения Отнош Значени ение я = = равно > больше > = больше или равно ~ = не равно

и логические операторы: Оператор Условие Запись в MATLAB Эквивалентная запись Логическое «и» x

Вернемся к нашему примеру, и заметим, что если ряд расходится, то условие на малость текущего слагаемого может никогда не выполнится и программа зациклиться. Поэтому ограничим число слагаемых 100. 000 Условие будет выглядеть так or (abs (x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10, k

Обработка исключительных ситуаций 1) break – прерывание цикла и выполнение оператора следующего за end (например, выход из внутреннего цикла); 2) Часть некорректных математических операций в MATLAB, не приводит к завершению работы программы (например, = inf, = Na. N). Выходом является конструкция try Операторы, выполнение которых может привести к ошибке catch Операторы в случае ошибки end 15

Операторы ветвления Условный оператор В MATLAB используются следующие операторы ветвления: n if – условный оператор; n switch – оператор переключения 16

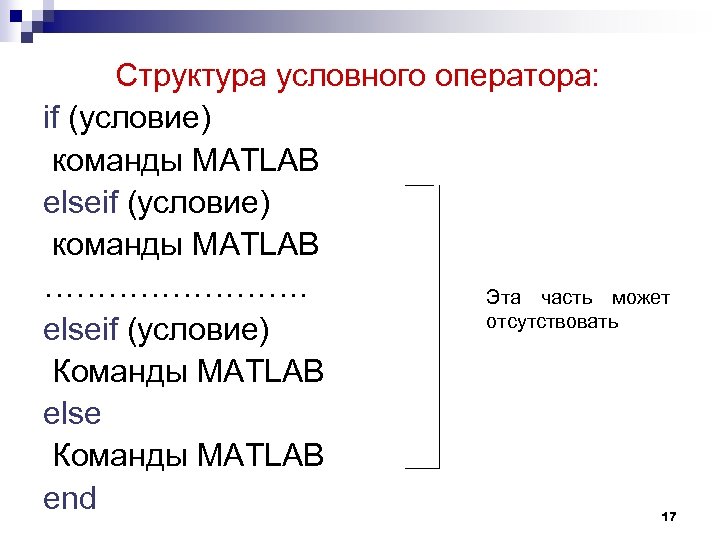Структура условного оператора: if (условие) команды MATLAB elseif (условие) команды MATLAB …………. Эта часть может отсутствовать elseif (условие) Команды MATLAB else Команды MATLAB end 17

При составлении М-файла, использующего операторы ветвления, полезно применять 1) команду warning (‘текст’) – для вывода предупреждения в командное окно; 2) функцию error (‘текст’) – для прекращения выполнения программы. 18

Пример 4 Дано квадратное уравнение ax 2 + bx +c = 0, a ≠ 0. Напишем М-функцию вычисляющую корни квадратного уравнения. Сделаем проверку на количество входных и выходных параметров, а так же на то, что входные параметры являются числами, а не векторами и матрицами. Более того, учтем случай комплексного корня. Программа выглядит так: 19

[x 1, x 2] = root 2 (a, b, c) if (nargin

Замечание Для написания собственных вычислительных программ большую пользу может принести самостоятельное изучение стандартных файл-функций в подкаталогах Toolbox. Большинство из них имеют открытый код, что позволяет понять принципы программирования в MATLAB. Другие функции (например, cos. m) являются встроенными. Они содержат комментарии об использовании функций. Приведем еще один пример. 21

Пример 5 Вычисление кусочно-заданной функции входным элементом, которой является матрица. Программа выглядит так: 22

y = kusfun (x) If nargin ~= 1 error (‘Должен быть один входной аргумент’) end [Nx, Mx] = size(x); y = zeros (size(x)); % инициализирует входной аргумент for i = 1 : Nx for j = 1 : Mx if x (i, j) = -pi не нужна! y (i, j) = x (i, j) / pi; else y (i, j) = – cos(x (i, j)) end end 23

Оператор switch удобно применять тогда, когда есть соответствие между дискретными значениями некоторой переменной и последующими действиями. 24

Структура оператора видна из следующего примера: switch a case -1 disp (‘a = -1’) case 0 disp (‘a = 0’) otherwise disp (‘a не равно -1, 0’) end 25

Оператор switch хорошо подходит для решения поставленной задачи о выводе различных графиков исследуемой функции (каркасная поверхность (а=1), линии уровня (а=2) и т. д. ). 26

Логические выражения с массивами и числами Универсальным способом обработки матричных данных служат логические операции. Поскольку MATLAB представляет числа массивами 1 1, то естественно ожидать, что массивы могут входить в логические выражения. Сейчас мы рассмотрим расширение логических операций и операций отношения на случай массивов. 27

Операции отношения Результат операции отношения в MATLAB может быть или логическая единица (‘истина’) или логический нуль (‘ложь’). Причем в отличие от многих языков программирования арифметические переменные могут использоваться в одном выражении с логическими. 28

Пример 6 • > a = 1; b = 3; c = 1; > a + (b > c) ans = 2 > a + (b

• > A = [1 2; 3 4]; B = [1 3; 4 5]; > C = A = = B C = 30

Замечание Так же как и в поэлементных арифметических операциях, допустимо использовать числа в качестве одного из аргументов операции отношения. В этом случае происходит сравнение каждого элемента массива с числом, результатом является массив того же размера, что и исходный. 31

Логические операции Применение логических операций к массивам приводит к поэлементному их выполнению над элементами массивов. n А and B – дает единицу, если соответствующие элементы не равны нулю; n A or B – дает единицу, если хотя бы один элемент не равен нулю; 32

not A – применяется к одному массиву, если элемент не равен нулю, то ставится нуль, иначе – единица; n all (v) – проверка наличия нулевых элементов в векторе, возвращает единицу, если нет нулевых элементов. Если v – матрица, то результат по столбцам; n any (v) – возвращает единицу, если во входном векторе есть хотя бы один ненулевой элемент. n 33

Приоритет операций 1. Отрицание; 2. Транспонирование, возведение в степень (в том числе поэлементное), знак плюс и минус перед числом; 3. Умножение и деление (в том числе поэлементное); 4. Сложение и вычитание; 5. Операции отношения; 6. Логическое ‘и’, логическое ‘или’. 34

Логическое индексирование Выделение части массива, элементы которого удовлетворяют определенному условию производится функцией find. 35

Пример 7 > a = [2 3 0 -1 0 3]; > u = find ((a = -1)) 3 4 5 > anew = a(u) 0 -1 0 36

Пример 8 Заменить самостоятельно элементы квадратной матрицы 5 x 5 случайных чисел из интервала (0, 1), больших среднего значения всех элементов на 10%, на среднее значение. Решение > A = rand (5); > S = sum (sum A) / 25; > A(find (A > S* 1. 1)) = S В данном случае функция find выдает 2 вектора номера строк и номера столбцов. 37

Полиномы в MATLAB Полином p (х) =anxn+an-1 xn-1+. . . +a 0, an≠ 0 в MATLAB задается вектор-строй р=[an, an-1, . . . , a 0] , где ai – любые комплексные числа, an≠ 0. Заметим, что степень полинома вычисляется так: n=length(р)-1 (при n=0 получается const). 38

Основные команд для действий с полиномами таковы: n n n r=roots(р) – вектор-столбец, содержащий все корни полинома; p=poly(r) – построение полинома по корням, заданным в векторе-столбце r, причем, если r квадратная матрица, то р – характеристический многочлен; y=polyval(p, x) – поэлементное вычисление у значений полиному р на множестве х, где х может быть вектором или матрицей; 39

n n n polyder(p) – вектор-строка, производная от p (дифференцирование полинома p); polyder(p, q) -производная от произведения полиномов p и q; [a, b]= polyder(p, q) – производная от частного полиномом p и q, где a и b являются числителем и знаменателем получившейся дроби; 40

n n n p=polyfit(x, y, n) – приближение функции y(x) полиномом p n-й степени по методу, минимизирующему расстояние между графиком полинома и истиной кривой, усредненное по всей их длине; conv(p, q) – вектор-строка, произведение полиномов p и q; [w, r]=deconv(p, q) – деление p на q, причем w-частное, r-остаток и p=conv (q, w) +r; 41

n [r, p, k]=residue(a, b) – разложение рациональной функции на простые дроби над полем комплексных чисел с выделением целой части k(х) или где ri – вычеты (элементы r), pi – полюса (элементы p). Эта команда работает и в обратную строну [a, b] =residue(r, p, k) 42

Замечание 1. Если в residue (a, b) полином b(х), а в roots(p) полином р(х) имеют кратные или близкие друг к другу корни, то результаты могут быть неверными, поскольку такая задача плохо обусловлена. Плохая обусловленность – это крайне сильная зависимость результата от коэффициентов (аналог устойчивости решения в дифференциальных уравнениях). 43

2. При работе с полиномами возникают полиномы вида [0, . . . ], а MATLAB автоматически не проверяет an≠ 0, и возникают ошибки (нужно самим следить). 44

Источник

Циклы и условия matlab: теория и примеры

Доброго времени суток. Сегодня речь пойдёт о циклах и условиях в Matlab. Материал, который взят за основу – это help в Matlab и несколько простых примеров, которые мы с вами и разберем.

Условия в MATLAB

Ни один язык программирования не обходится без таких конструкций как условия, именно об этом мы с вами и поговорим:

Начнём с синтаксиса условия if и посмотрим на формальный вариант записи в справке:

if expression, ements, end

Что значит:

if Условие, Действие, end

Теперь примеры:

x = 1; y = 61; if ((x >= 0.90) && (y >= 60)) disp(‘ok’); end;

&& – логически оператор умножения (логическая «И»).

И вот пример с else:

x = 1; y = 50; if ((x >= 0.90) && (y >= 60)) disp(‘ok’); else disp(‘not right’) end;

В отличие от 1 примера, здесь выведется «not right».

Пару слов теперь о switch. Формально в справке:

Syntax switch switch_expr case case_expr ement, …, ement case {case_expr1, case_expr2, case_expr3, …} ement, …, ement otherwise ement, …, ement end

Более приземлённо:

Syntax switch switch_expr case Значение – 1 Действие case {Зачение – 2, Знчение – 3, Значение – 4, …} Действие В остальных случиях Действие end

Это значит, что если заданная переменная равна значению в case Значение – 1, то выполняется действие при case Значение – 1 и так далее. Если ни один из case не подошёл выполняется действие при otherwise.

Вот пример:

method = ‘Bilinear’; switch lower(method) case {‘linear’,’bilinear’} disp(‘Method is linear’) case ‘cubic’ disp(‘Method is cubic’) case ‘nearest’ disp(‘Method is nearest’) otherwise disp(‘Unknown method.’) end

Циклы в MATLAB

Теперь перейдём к циклам, начнём с for.

В справке это записано в виде

Syntax for index = values program ements : end

В приземлённом виде это значит:

Syntax for переменная = значению действие end

Не будем задерживаться на официальных формулировках, лучше к понятным и любимым примерам

for m = 1:10 m end

Вот так выглядит самый распространённый способ использования for. В этом цикле мы просто выводим значение m.

Второй способ с использованием шага (step)

for s = 1.0: -0.1: 0.0 disp(s) end

В данном случае цикл for идёт от 1 до 0 с шагом -0.1.

Ещё один вариант:

for s = [1,5,8,17] disp(s) end

В данном случае переменная s будет последовательно приравниваться 1, 5 ,8 , 17 и, соответственно, выводиться.

А также с for очень удобно выводить вектора. Вот:

for e = eye(5) disp(‘Current value of e:’) disp(e) end

В данном примере идёт последовательное обращение к элементам вектора e.

Цикл while:

Формально в справке:

Syntax while expression program ements : end

Приземлённо:

Syntax while Условие Действие end

И давайте сразу к примеру (как это в реальной жизни используется).

eps = 10; while eps > 1 eps = eps – 1 end

Пока в условие (eps > 1) выполняется, цикл выполняет действие

(eps = eps-1).

Также в условии while можно использовать логические операторы И – && и ИЛИ – ||, записывая несколько логических выражений в условие.

Если есть вопросы по статье, пишите в комментариях.

Поделиться ссылкой:

Похожее

codetown.ru

Циклы for, while в Матлаб(Matlab)

Оператор for предназначен для выполнения заданного числа повторяющихся действий. Самое простое использование оператора for осуществляется следующим образом:

for count = start:step:final команды MatLab end

Здесь count – переменная цикла, start – ее начальное значение, final – конечное значение, а step – шаг, на который увеличивается count при каждом следующем заходе в цикл. Цикл заканчивается, как только значение count становится больше final. Переменная цикла может принимать не только целые, но и вещественные значения любого знака

Цикл for оказывается полезным при выполнении повторяющихся похожих действий в том случае, когда их число заранее определено. Обойти это ограничение позволяет более гибкий цикл while.

while условие циклакоманды MatLab end

62. Какой командой создается М-книга в текстовом редакторе Word, связанном сMatLab?

Начало новой М-книги Чтобы приступить к написанию новой М-книги, нужно: 1) запустить редактор Word; 2) выбрать в диалоговом окне WordопциюNewиз менюFile; 3) в окне, которое появится на экране, выбрать шаблон M-book. В результате этих действий будет запущена системаMatLAB, и вид глав- ного меню редактора Word несколько изменится – в нем появится новое менюNotebook. Это и будет свидетельствовать, что кWordприсоединена системаMatLAB. Если теперь с помощью мыши активизировать менюNotebookокнаWord, на экране появится дополнительное меню

63. Какая команда в текстовом редакторе Word преобразует текст в ячейку ввода MatLab?

выбрать команду Define Input Cell(Определить Входную Ячейку) в ме- нюNotebook(см. рис. 3.20), или нажать клавиши ; после этого вид стро- ки команды должен измениться – символы команды приобретают темно-зеленый цвет, а команда становится отороченной квадратными скобками темно-серого цвета;@

64. Какая команда в текстовом редакторе Word обеспечивает в ячейке выполнение команды MatLab?

выбрать мышкой команду Evaluate Cell (Вычислить ячейку), или нажать комбинацию клавиш ; результатом этих действий должно стать появ- ление сразу после текста команды результатов ее выполнения системой MatLAB. Результаты выполнения команды выводятся, синим цветом и взяты в квад- ратные скобки

65. Какая команда в текстовом редакторе Word обеспечивает выполнение команд MatLab во всей М-книге?

Выполнение команд всех ячеек или групп ячеек ввода раздела произ- водится при помощи пункта Evaluate Calc Zone, а сразу всей М-книги – Evaluate М-book

66. Какая команда в текстовом редакторе Word обеспечивает выполнение команд MatLab во всех ячейках автоматически при открытии М-книги?

Команды ячеек, имею- щих стиль Autolnit, запускаются сразу после открытия М-книги. Полезно включить в первую такую ячейку команду clear для очистки рабочей среды. Для установки стиля Autolnit служит пункт Define Autoinit Cell меню Notebook

67. Какие кнопки содержит панель Excel в электронной таблице Excel при их связи с MatLab?

68. Что обеспечивает команда putmatrix?

Функция MLPutMatrix служит для по- мещения данных из ячеек рабочего листа Excel в массив рабочей среды Matlab. Аргументами данной функции являются имя переменной, заключен- ное в кавычки, и диапазон ячеек Excel, относящихся к этой переменной

68. Что обеспечивает команда getmatrix?

Об- ратную операцию осуществляет функция MLGetMatrix, при этом аргу- ментами этой функции являются имя переменной рабочей среды MatLab с 22 данными, заключенной в кавычки, и диапазон ячеек Excel, где будут разме- щены данные этой переменной, также заключенный в кавычки.

70. Для чего предназначен пакет Simu?

В состав системы Matlab входит пакет моделирования динамических систем – Simu. Данный пакет является ядром интерактивного программ- ного комплекса, предназначенного для математического моделирования ли- нейных и нелинейных динамических систем, представленных своей функ- циональной блок-схемой, именуемой S -моделью или просто моделью

71. Какая библиотека Simu содержит источники сигналов?

Построим простейшую модель источника синусоидального сигнала, который подается на вход виртуального осциллографа. Для этого щелкнем на кнопке открытия браузера библиотек и в левой части появившегося окна браузера щелкнем на разделе Sources(Источники), при этом в правой части окна отображаются пиктограммы блоков, входящих в данный раздел

72. Какая библиотека Simu содержит регистрирующие виртуальные приборы?

осциллограф Scope из раздела Sinks.

73. Какая библиотека Simu содержит блоки дифференцирования и интегрирования?

Continuous содержит непрерывные блоки. К числу важнейших относятся блоки дифференцирования Derivative и интегрирова- ния Integrator. Первый блок осуществляет численное дифференцирование входного сигнала, для данного блока никакие параметры не вводятся. Вто- рой блок в окне параметров содержит несколько полей, в котором можно задать постоянную интегрирования на выходе блока в поле Initial condition

74. Какая библиотека Simu содержит блоки вычисления элементарных функций?

Окно библиотеки Mathсодержит блоки выполнения математических операций

К блокам вычисления элементарных функций относятся три блока: блок математических функций Math, блок тригонометрических функцийTrigonometricи блок функций округленияRounding .

75. Сколько значений параметров шага устанавливается в Simu при переменном шаге моделирования?

Большое значение имеют две опции решателя в поле Solver options: тип решения и метод решения. Возможны два варианта первой опции:

• Variable-step solvers – решение с переменным шагом;

• Fixed-step solvers – решение с фиксированным шагом. По умолчанию установлена опция решения с переменным шагом, ко- гда шаг автоматически уменьшается при увеличении скорости изменения результатов и наоборот. Обычно этот метод дает лучшие результаты, чем моделирование с фиксированным шагом, исключая в большинстве случаев расхождение результатов. Применение моделирования с фиксированным шагом применяется обычно в том случае, если это обусловлено спецификой решаемой задачи

studfiles.net

Циклы типа for…end MatLab

Урок 20. Основы программирования Основные понятия программирования

Основные средства программирования

Основные типы данных

Виды программирования

Двойственность операторов, команд и функций

Некоторые ограничения

М-файлы сценариев и функций

Структура и свойства файлов сценариев

Статус переменных в функциях

Структура М-файла-функции

Статус переменных и команда global

Использование подфункций

Частные каталоги

Обработка ошибок

Вывод сообщений об ошибках

Функция lasterr и обработка ошибок

Функции с переменным числом аргументов

Функции подсчета числа аргументов

Переменные varargin и varargout

Комментарии

Особенности выполнения m-файлов функций

Создание Р-кодов

Управляющие структуры

Диалоговый ввод

Условный оператор

Циклы типа for…end

Циклы типа while…end

Конструкция переключателя

Конструкция try…catch…end

Создание паузы в вычислениях

Понятие об объектно-ориентированном программировании

Создание класса или объекта

Проверка принадлежности объекта к заданному классу

Другие функции объектно-ориентированного программирования

Что нового мы узнали?

Циклы типа for…end обычно используются для организации вычислений с заданным числом повторяющихся циклов. Конструкция такого цикла имеет следующий вид:

for vаг=Выражение. Инструкция. …. Инструкция end

Выражение чаще всего записывается в виде s:d:e, где s – начальное значение переменной цикла var, d – приращение этой переменной и е – конечное значение управляющей переменной, при достижении которого цикл завершается. Возможна и запись в виде s :е (в этом случае d=l). Список выполняемых в цикле инструкций завершается оператором end.

Следующие примеры поясняют применение цикла для получения квадратов значений переменной цикла:

» for 1=1:5 i^2. end;

ans =

» for x=0:.25:1 Х ^ 2, end:

ans =

0.0625

ans =

0.2500

ans =

0.5625

ans =

Оператор continue передает управление в следующую итерацию цикла, пропуская операторы, которые записаны за ним, причем во вложенном цикле он передает управление на следующую итерацию основного цикла. Оператор break может использоваться для досрочного прерывания выполнения цикла. Как только он встречается в программе, цикл прерывается. Возможны вложенные циклы, например:

for i=1:3

for j=l:3

A(1.j)=i+j;

end

В результате выполнения этого цикла (файл for2.m) формируется матрица А:

» for2

» А

А =

2 3 4

3 4 5

4 5 6

Следует отметить, что формирование матриц с помощью оператора : (двоеточие) обычно занимает намного меньше времени, чем с помощью цикла. Однако применение цикла нередко оказывается более наглядным и понятным. MATLAB допускает использование в качестве переменной цикла массива А размера тхп. При этом цикл выполняется столько раз, сколько столбцов в массиве А, и на каждом шаге переменная var представляет собой вектор, соответствующий текущему столбцу массива А:

» А=[1 2 3:4 5 6]

А =

1 2 3

4 5 6

» for var=A; var, end

var =

var=

radiomaster.ru

Иллюстрированный самоучитель по MatLab › Основы программирования › Циклы типа for…end. Циклы типа while…end. [страница – 364] | Самоучители по математическим пакетам

Циклы типа for…end. Циклы типа while…end.

for var=Выражение. Инструкция….. Инструкция end

Выражение чаще всего записывается в виде s:d:e, где s – начальное значение переменной цикла var, d – приращение этой переменной и е – конечное значение управляющей переменной, при достижении которого цикл завершается. Возможна и запись в виде s:е (в этом случае d=1). Список выполняемых в цикле инструкций завершается оператором end.

Следующие примеры поясняют применение цикла для получения квадратов значений переменной цикла:

>> for 1=1:5 i^2, end;

ans =

>> for x=0:.25:1 X ^ 2, end:

ans =

0.0625

ans =

0.2500

ans =

0.5625

ans =

for i=1:3

for j=i:3

A(1.j)=i+j;

end

В результате выполнения этого цикла (файл for2.m) формируется матрица А:

>> for2

>> A

A =

2 3 4

3 4 5

4 5 6

Следует отметить, что формирование матриц с помощью оператора: (двоеточие) обычно занимает намного меньше времени, чем с помощью цикла. Однако применение цикла нередко оказывается более наглядным и понятным. MATLAB допускает использование в качестве переменной цикла массива А размера тхп. При этом цикл выполняется столько раз, сколько столбцов в массиве А, и на каждом шаге переменная var представляет собой вектор, соответствующий текущему столбцу массива А:

>> A=[1 2 3:4 5 6]

A =

1 2 3

4 5 6

>> for var=A; var, end

var =

var=

Циклы типа while…end

Цикл типа while выполняется до тех пор, пока выполняется Условие:

while Условие Инструкции end

Пример применения цикла while уже приводился. Досрочное завершение циклов реализуется с помощью операторов break или continue.

samoychiteli.ru

Источник